ЕГЭ математика 2017. Разбор варианта Алекса Ларина № 194
Подробный разбор 1-12 задания тренировочного варианта ЕГЭ № 194 Ларина
Подробный разбор 13,14,15,16,17,18,19 задания тренировочного варианта ЕГЭ № 194 Ларина
Задание 1
Для консервации овощей хозяйка готовит столовый уксус: к 100 мл 70‐% уксусной кислоты (эссенции) добавляет 700 мл воды. Определите процентное содержание уксусной кислоты в полученном растворе.
В 100 мл содержится 70%, то есть в мл это будет 100*,07=70 мл. Новый раствор по массе равен 100+700=800 мл. Составим пропорцию: 800 - 100% 70 - x% x = 100*70/800=8.75
Задание 2
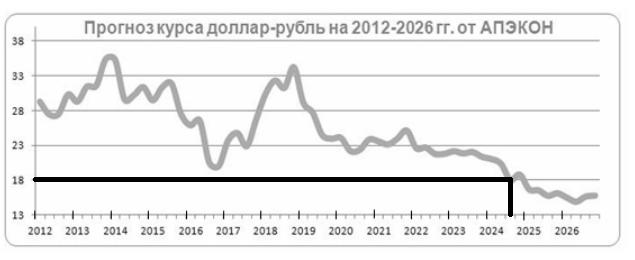
В 2010‐м году Агентство прогнозирования экономики (АПЭКОН) представило прогноз курса доллара по отношению к рублю на 2012‐2026 годы. На рисунке приведена прогнозируемая стоимость 1 доллара в рублях. В каком году, по мнению экспертов из АПЭКОН, доллар впервые упадет ниже отметки 18 рублей за 1 доллар?
Проведем линию через ординату 18 и получим пересечение с графиком между абсциссами 2024 и 2025. Значит ответ будет 2024
Задание 3
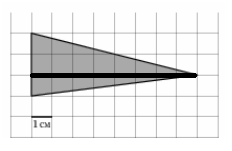
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см * 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Построим высоты в треугольнике, она будет равна 8. Основание при этом равно 3. Площадь треугольника равна половине произведения основания на высоту: S = 0.5 * 3 * 8 = 12
Задание 4
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что все семь мальчиков будут сидеть рядом.
Рассмотрим эту же ситуацию, но под другим ракурсом. Если все мальчики сидят рядом, то девочки тоже сидят рядом. Найдем вероятность того, что две девочки окажутся рядом. Около девочки два стула. На один стул претендуют 7 мальчиков и 1 девочка, то есть 8 человек. Следовательно, вероятность того, что девочка сядет на этот стул 1/8 = 0,125. При этом стула два (справа и слева), значит умножим полученную вероятность на 2: 0.125 * 2 = 0.25. Получаем, что вероятность того, что девочки окажутся рядом, а значит и все мальчики рядом = 0,25
Задание 5
Найдите корень уравнения $$\log _{2} (-x) + \log _{2} (2-x) = 3$$ .Если корней несколько, то в ответе укажите их сумму.
$$\log _{2} (-x) + \log _{2} (2-x) = 3$$
$$-x > 0 ; 2 - x > 0 \Leftrightarrow x<0$$
$$\log _{2} ((-x) *(2-x)) = \log _{2} 8$$
$$-2x+x^2=8$$
$$x^2-2x-8=0$$
$$x_1=4 - не входит в ОДЗ ; x_2 =-2$$
Задание 6
|
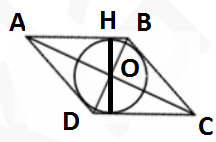
Площадь ромба вычисляется как половина произведения диагоналей. То есть $$S = 0.5 *2\sqrt{5}*4\sqrt{5}=20$$ С другой стороны, площадь равна произведению основания на высоту, а высота равна двум радиусам вписанной окружности. То есть S = AB * 2 OH = AB * 2r Найдем AB по теореме Пифагора из треугольника ABO (его катеты равны половинам диагоналей): $$AB = \sqrt{\sqrt{5}^{2}+2\sqrt{5}^{2}}=\sqrt{5+20}=5$$ Приравняем площади: 20 = 5 * 2r, r = 2 |
Задание 7
Производная непрерывной функции f (x) равна нулю в каждой точке отрезка [‐5; 4]. Известно, что f (– 5) = – 5. Найдите f (4)
Раз производная равна нулю на всем промежутке и функция непрерывна, то функция не возрастает и не убывает, то есть сохраняет свое значение. Значит f(– 5) =f(4)= – 5
Задание 8
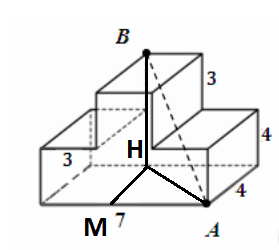
В многограннике, приведенном на рисунке, все двугранные углы прямые. Найдите расстояние между точками А и В.
Для этого рассмотрим прямоугольный треугольник BHA: BH = 3 + 4 = 7. HA неизвестно, найдем ее из треугольника прямоугольного HMA: $$HA = \sqrt{HM^2+MA^2}$$
$$HA = \sqrt{HM^2+MA^2}=\sqrt{4^2+(7-3)^2}=\sqrt{32}$$
$$AB = \sqrt{BH^2+AH^2}=\sqrt{7^2+\sqrt{32}^2}=\sqrt{49+32}=\sqrt{81}=9$$
Задание 9
Найдите значение выражения $$\frac{(0.1)^{-1}-(0.1)^{0}}{(\frac{3^{2}}{2^{3}})^{-1}*(\frac{3}{2})^{3}-(\frac{1}{3})^{-2}}$$
$$\frac{(0.1)^{-1}-(0.1)^{0}}{(\frac{3^{2}}{2^{3}})^{-1}*(\frac{3}{2})^{3}-(\frac{1}{3})^{-2}}=$$ $$=\frac{10-1}{\frac{2^{3}}{3^{2}}*\frac{27}{8}-9}=\frac{9}{\frac{8}{9}*\frac{27}{8}-9}=$$ $$\frac{9}{3-9}=\frac{9}{-6}=-1.5$$
Задание 10
Объём и давление идеального газа при постоянных температуре и массе связаны между собой законом Бойля‐Мариотта: pV=C (р – давление в Па, V – объём в м3 , C – некоторая постоянная). Газ, находившийся в сосуде объёмом 5 м3под давлением 1 кПа, сжали до объёма 4 м3. Каким (в Па) стало давление газа?
пусть p1=1кПа, V1=5 м3, V2=4 м3, p2 - новое давление в кПа
$$p_1*V_1=p_2*V_2 \Leftrightarrow $$
$$5*1=4*p_2 \Leftrightarrow $$
$$p_2=\frac{5}{4}=1.25$$ кПа $$=1250$$ Па
Задание 11
На реке расположены пункты А и Б. Известно, что из А в Б баржа плывет 4 часа, а из Б в А – 6 часов. За какое время из пункта А в пункт Б доберется плот? Ответ дайте в часах.
Пусть x- скорость баржи в стоячей воде. у - скорость течения и s - расстояние между пунктами, примем его за 1. Тогда, $$t_1=\frac{1}{x+y}=4 ; t_2=\frac{1}{x-y}=6 \Leftrightarrow x+y = 1/4 ; x-y=1/6$$
Вычтем из первого уравнения второе и получим: $$ 2y=1/12 \Leftrightarrow y=1/24$$
То есть скорость течения составляет одну двадцать четвертую от расстояния, а плот двигается только со скоростью течения, значит расстояние пройдет за 24 часа
Задание 12
Найдите критическую (стационарную) точку функции $$y=3x^{4}+8x^{3}+6x^{2}+1$$ , которая не является точкой экстремума.
Найдем производную данной функции: $$y=3x^{4}+8x^{3}+6x^{2}+1\Leftrightarrow y^{'}=12x^{3}+24x^{2}+12x\Leftrightarrow$$ Приравняем производную к нулю:
$$12x^{3}+24x^{2}+12x=0 \Leftrightarrow x(12x^{2}+24x+12)=0 \Leftrightarrow $$
$$\left\{\begin{matrix}x = 0\\ 12(x^{2}+2x+1)=0\end{matrix}\right.\Leftrightarrow $$
$$\left\{\begin{matrix}x = 0\\ (x+1)^{2}=0\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}x = 0\\ x=-1\end{matrix}\right.$$
| Начертим координатную прямую и отметим полученные точки на ней. Подставим в производную значения с каждого интервала, чтобы определеить знаки. Как видим, слева и справа от x = -1 одинаковые значения производной, значит это и есть критическая точка не являющаяся экстремумом |
Задание 13
Дано уравнение $$\frac{\sin 2x-1+2\cos x-\sin x}{\sqrt{-\sin x}}=0$$.
Задание 14
В правильной четырехугольной призме $$ABCDA_{1}B_{1}C_{1}D_{1}$$ $$AB=BC=8$$, $$AA_{1} = 6$$. Через точки $$A$$ и $$C$$ перпендикулярно $$BD_{1}$$ проведена плоскость Ω.
Задание 16
Точки $$M$$ и $$P$$ – середины сторон $$BC$$ и $$AD$$ выпуклого четырехугольника $$ABCD$$. Диагональ $$AC$$ проходит через середину отрезка $$MP$$.
Задание 17
На покупку тетрадей в клетку и в линейку можно затратить не более 140 рублей. Тетрадь в клетку стоит 3 руб., в линейку – 2 руб. Число купленных тетрадей в клетку не должно отличаться от числа тетрадей в линейку более, чем на 9. Необходимо купить максимально возможное суммарное количество тетрадей, при этом тетрадей в линейку нужно купить как можно меньше. Сколько тетрадей в клетку и сколько в линейку можно купить при указанных условиях?
Задание 19
Пусть $$S_{n}$$ – сумма $$n$$ первых членов арифметической прогрессии $$(a_{n})$$. Известно, что $$S_{n+1}=2n^{2}-21n-23$$.