369 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$3^x+3\sqrt{27^x}=3\cdot7^x+\sqrt{21^x}$$
$$3^x-3\cdot7^x+2\sqrt{27^x}=0$$
Сделаем замену $$a=3^{\frac{x}{2}}$$ и $$b=7^{\frac{x}{2}}$$
Тогда уравнение перепишется:
$$a^2−3b^2+2ab=0$$
Не трудно выделить полный квадрат:
$$a^2+2ab+b^2−4b^2=0$$
$$(a+b)^2=4b^2$$
Очевидно, чтобы равенство выполнялось нужно потребовать $$a=b$$
Делаем обратную замену:
$$3^{\frac{x}{2}}=7^{\frac{x}{2}}$$
$$(\frac{3}{7})^{\frac{x}{2}}=1$$
$$\frac{x}{2}=0$$
$$x=0$$
Задание 2
$$A$$ – первый раз попал
$$B$$ – первый раз промах, второй раз попал
$$P(A+B)=P(A)+P(B)=0,8+(1-0,8)\cdot0,8=0,96$$
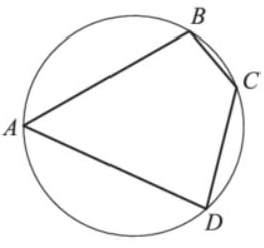
Задание 3
$$AB=4x, BC=2x, CD=3x, AD=6x$$
В сумме эти дуги дают $$360^{\circ}$$
$$AB+BC+CD+AD=360^{\circ}$$
$$15x=360$$
$$x=24$$
Угол BAD опирается на дугу $$BD=5x=120^{\circ}$$
Значит сам угол $$BAD=60^{\circ}$$ (половина градусной меры дуги)
Задание 4
$$17-12\sqrt{2}=(9-12\sqrt{2}+8)=(3-2\sqrt{2})^2$$
Теперь рассмотрим
$$3-2\sqrt{2}=2-2\sqrt{2}+1=(\sqrt{2}-1)^2$$
Значит
$$\log_{\sqrt{2}-1}(17-12\sqrt{2})=\log_{\sqrt{2}-1}(\sqrt{2}-1)^4=4$$
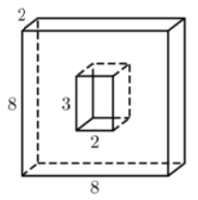
Задание 5
$$S_{всего}=8\cdot8\cdot2+8\cdot2\cdot4=192$$
Площадь с вырезанным многогранником
$$S=192−3\cdot2\cdot2+2\cdot2\cdot2+3\cdot2\cdot2=200$$
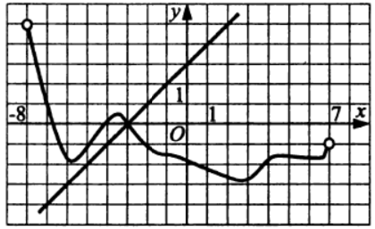
Задание 6
$$f'(x_0)=\tg\alpha=1$$
Проведем $$y=1,$$ видим одну точку пересечения, значит $$x_0=-7$$
$$y_{кас}=f(x_0)+f'(x_0)(x−x_0)=f(x_0)+x+7$$
Так как касательная – это прямая, то ее вид $$y=kx+b,$$ откуда видно, что $$b=f(x_0)+7$$
Его не трудно найти из графика $$b=3$$
$$f(x_0)=3-7=-4$$
$$x_0+f(x_0)=-7+(-4)=-11$$
Задание 7
$$v=20\cos\frac{2\pi131}{6}=20\cos(43\pi+\frac{2\pi}{3})=-20\cos\frac{2\pi}{3}=-20\cdot\frac{1}{2}=-10$$
$$E=\frac{0,16\cdot10^2}{2}=8$$
Задание 8
Пусть масса первого и второго раствора равны $$x$$ и $$y$$ соответственно
$$0,3\cdot x+0,5\cdot3+0,9\cdot y=0,75(x+3+y)$$
$$0,3\cdot x+0,9\cdot3=0,75\cdot(x+3)$$
Решая систему получаем ответ
$$(x,y)=(1,8)$$
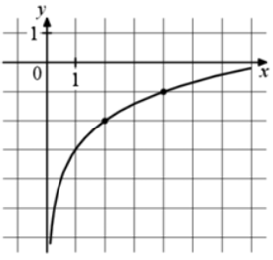
Задание 9
По рисунку видно, что логарифмическую функцию опустили на 3 единицы вниз, т.е.
$$f(x)=\log_a x-3$$
Коэффициент $$a$$ легко найти, если подставить какую-нибудь точку
$$f(x)=\log_2 x−3$$
$$f(x)=1$$ будет при $$x=16$$
Задание 10
Задание 11
ОДЗ:
$$x>0$$
Найдем критические точки:
$$f'(x)=0$$
$$-2x-1+\frac{1}{x}=0$$
$$\frac{-2x^2-x}{x}=0$$
$$-2x^2-x+1=0$$
$$x=-1$$ – не подходит под ОДЗ
$$x=0,5$$
По методу интервалов $$x=0,5$$ – точка максимума