403 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
Задание 1
Задание 2
$$\rho(C_1;BA_1)=h,$$ где $$h$$ - высота $$\Delta C_1BA_1,$$ опущенная из $$C_1.$$
Из $$\Delta A_1C_1D_1:$$
$$C_1A_1=\sqrt{(\sqrt{6})^2+(\sqrt{6})^2}=\sqrt{12}$$
$$\Delta C_1BA_1$$ - равносторонний, тогда $$h=C_1\cdot\sin C_1BA_1=\sqrt{12}\cdot\frac{\sqrt{3}}{2}=3$$
Задание 3
Нижние небоковые места имеют нечетные номера в диапазоне от 1 до 36. Таких чисел 18.
$$P(A)=\frac{18}{54}=\frac{1}{3}\approx0,33$$
Задание 4
1. Рассматриваем следующие события и гипотезы:
•событие $$А$$ = {болванка без дефекта};
•гипотеза $$Н_1$$ = {болванка изготовлена первым цехом}, $$Р(Н_1)=70\%=0,7$$
•гипотеза $$Н_2$$ = {болванка изготовлена вторым цехом}, $$Р(Н_2)=30\%=0,3$$
2. Так как литье первого цеха имеет 10% брака, то 90% болванок, изготовленных первым цехом, не имеют дефекта, т.е. $$РН_1(А)=0,9.$$
Литье второго цеха имеет 20% брака, то 80% болванок, изготовленных вторым цехом, не имеют дефекта, т.е. $$РН_2(А)=0,8.$$
3. По формулу Бейеса найдем $$РА(Н_1)=0,7\cdot\frac{0,9}{(0,7\cdot0,9+0,3\cdot0,8)}=\frac{0,63}{0,87}\approx0,72$$
Задание 5
$$\frac{\sqrt{x^2-25}-12}{\sqrt{-3x}}=0\Leftrightarrow\left\{\begin{matrix} x^2-25=144\\ -3x>0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x=\pm13\\ x<0 \end{matrix}\right.\Leftrightarrow x=-13$$
Задание 6
$$\log_a\sqrt[5]{a^4b^3}=\frac{1}{5}\log_a a^4b^3=\frac{1}{5}(\log_a a^4+\log_a b^3)=\frac{1}{5}(4+3\log_a b)=\frac{1}{5}(4+\frac{3}{\log_b a})=$$
$$=\frac{1}{5}(4+3:(-\frac{1}{3}))=\frac{1}{5}\cdot(-5)=-1$$
Задание 7
Известно, что производная положительная в окрестностях точек, где функция возрастает и отрицательная, где функция убывает. Анализ графика производной показывает, что на участке $$[-5;-3]$$ функция $$f(x)$$ возрастала, а затем, на участке $$[-3; 0]$$ – убывала. Следовательно, максимальное значение она приобретает в точке $$-3.$$
Задание 8
Выразим квадрат синуса из формулы энергии:
$$\sin^\alpha=\frac{Q}{mv^2}$$
Подставим сюда числовые величины, получим:
$$\sin^2\alpha=\frac{50}{2\cdot10^2}=\frac{1}{4}$$
откуда
$$\sin\alpha=\pm\frac{1}{2}$$
В задаче спрашивают наименьший угол и в физике углы берутся из положительной области, поэтому имеем уравнение
$$\sin\alpha=\frac{1}{2}\Rightarrow \alpha=\arcsin\frac{1}{2}=30^{\circ}$$
И, окончательно, угол $$2\alpha=2\cdot30^{\circ}=60^{\circ}.$$
Задание 9
Пусть $$x$$ км в час – собственная скорость байдарки, тогда
$$(x+3)$$ км в час – скорость байдарки по течению,
$$(x–3)$$ км в час – скорость байдарки против течения.
$$\frac{15}{x+3}$$ час. – время в пути по течению
$$\frac{15}{x–3}$$ час. – время в пути против течения.
Всего байдарка была в движении ( по течению и против течения)
18:00 - 10:00 - 1 час 20 мин (стоянки) = 6 часов 40 мин = $$6\frac{2}{3}$$ = $$\frac{20}{3}$$
$$\frac{15}{x+3}+\frac{15}{x–3}=\frac{20}{3}$$
Делим на 5:
$$\frac{3}{x+3}+\frac{3}{x–3}=\frac{4}{3}$$
$$9x–27+9x+27=4(x^2–9)$$
$$4x^2–18x–36=0$$
$$2x^2–9x–18=0$$
$$D=(-9)^2-4\cdot2\cdot(-18)=81+144=225$$
$$x_1=\frac{9+15}{4}=6$$
Второй корень отрицательный и не удовлетворяет смыслу задачи.
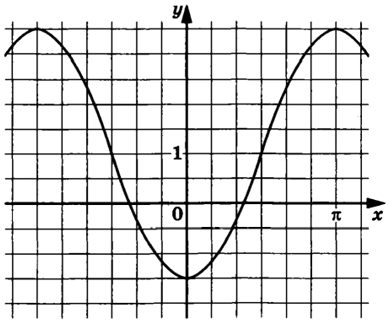
Задание 10
График проходит через $$(0;-1,5)$$ и $$(\frac{\pi}{2};1).$$ Тогда:
$$\left\{\begin{matrix} -1,5=a\cdot\cos0+b\\ 1=a\cdot\cos\frac{\pi}{2}+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -1,5=a+b\\ b=1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=-2,5\\ b=1 \end{matrix}\right.$$
Задание 11
$$y=\ln(x+9)-10x+7$$
$$y'=\frac{1}{x+9}-10$$
$$\frac{1}{x+9}-10=0$$
$$\frac{1}{x+9}=10$$
$$10x+90=1$$
$$10x=-89$$
$$x=-8,9$$
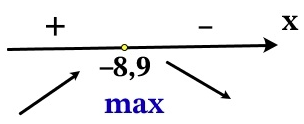
Определим знаки производной функции и изобразим поведение функции:
Точка максимума функции: $$x=-8,9.$$