248 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Решаем ЕГЭ 248 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №248 (alexlarin.com)
Решаем ЕГЭ 248 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №248 (alexlarin.com)
Задание 1
В доме, в котором живет Слава, 14 этажей и несколько подъездов. Во всех подъездах на каждом этаже находится по 6 квартир. Слава живет в квартире номер 322. Определите номер подъезда, в котором живет Слава.
В одном подъезде 14*6=84 квартиры
Номер подъезда : $$\frac{322}{84}\approx 3,8\Rightarrow 4$$
Задание 2
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 18 февраля. Ответ дайте в градусах Цельсия.
Наибольшая температура 18 февраля была с 12:00 по 18:00 и составляла -7
Задание 3
Найдем длины диагоналей:
$$AC=\sqrt{(5-1)^{2}+(5-1)^{2}}=\sqrt{32}$$
$$BD=\sqrt{(4-2)^{2}+(2-4)^{2}}=\sqrt{8}$$
Найдем площадь ромба:
$$S=\frac{1}{2}AC*BD=$$$$\frac{1}{2}\sqrt{32}\sqrt{8}=$$$$\frac{1}{2}\sqrt{2^{5}*2^{3}}=$$$$\frac{1}{2}*2^{4}=8$$
Задание 4
Квадратный лист бумаги со стороной 10 см разбивают на 100 квадратиков со стороной 1 см и среди этих квадратиков случайным образом выбирают один. Какова вероятность, что расстояние от одной из сторон выбранного квадратика до границы листа составит не более 3 см?
Если взять расстояние от сторон в 3 клетки, то получим квадрат FGHE. Но расстояние от сторон его составляет 3 квадрата, то есть пападает в условие не более трех. Тогда убираем еще по одному квадрату и получаем квадрат IJKE. Его площадь 2*2=4.
Тогда площадь оставшейся части :100-4=96.
Тогда вероятность составит: $$P=\frac{96}{100}=0,96$$
Задание 5
Найдите корень уравнения $$\sin \frac{\pi(x+9)}{4}=-\frac{\sqrt{2}}{2}$$ . В ответе напишите наименьший положительный корень.
Найдем значение х:
$$\left[\begin{matrix}\frac{\pi(x+9)}{4}=-\frac{\pi}{4} +2\pi n , n \in Z|:\frac{\pi}{4}\\\frac{\pi(x+9)}{4}=-\frac{3\pi}{4} +2\pi n , n \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x+9=-1+8n\\x+9=-3+8n\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=-10+8n\\x=-12+8n, n \in Z\end{matrix}\right.$$
Найдем наименьший положительный для первого корня: $$-12+8n>0\Leftrightarrow$$ $$8n>12\Leftrightarrow$$ $$n>\pm 1,5$$. Тогда, наименьшее n при котором выйдет наименьший положительный корень составит 2: При $$n=2: x=-12+8*2=4$$
Найдем наименьший положительный для второго корня:$$-10+8n>0\Leftrightarrow$$ $$8n>10\Leftrightarrow$$ $$n>1\frac{1}{4}$$, тогда, наименьшее n при котором выйдет наименьший положительный корень составит 2: при n=2 $$x=-10+8*2=6$$
Как видим, наименьший положительный корень равен 4
Задание 6
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите больший угол трапеции. Ответ дайте в градусах.
1) Пусть $$\angle DBA=\alpha$$, тогда из $$\Delta ABD:\angle A=90-\alpha$$
2) $$\angle DBA=\angle CDB=\alpha$$ (накрест лежащие ), тогда $$\angle ADC=90+\alpha$$
3) $$\angle ADC=\angle DCB\Rightarrow$$ из $$\Delta DCB: \angle CDB=\frac{180-(90+\alpha )}{2}=$$$$45-\frac{\alpha }{2}$$, но $$\angle CDB=\alpha$$. Тогда: $$45-\frac{\alpha }{2}=\alpha \Leftrightarrow$$ $$45=\frac{3\alpha }{2}\Leftrightarrow$$ $$\alpha=30$$
4) $$\angle A=810+90-\alpha =60$$, тогда $$\angle D=180-\angle A=120$$
Задание 7
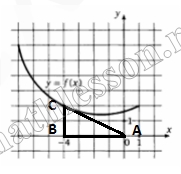
На рисунке изображен график функции $$f(x)$$ . Касательная к этому графику, проведенная в точке с абсциссой ‐4 проходит через начало координат. Найдите $$f'(-4)$$
Рассмотрим $$\Delta ABC: tg\angle A=-{f}'(-4)$$
$$tg\angle A=\frac{CB}{AB}=$$$$\frac{2}{4}=\frac{1}{2}\Rightarrow$$ $${f}'(-4)=-0,5$$
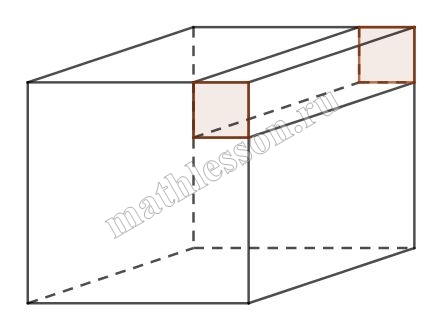
Задание 8
В данном случае можно рассматривать фигуру, как параллелограмм (4*3*4), у которого вырезаны на передней и задней грани два квадрата со стороной 1.
Тогда площадь его поверхности составит: $$S=4*4*2+4*3*4-1*1*1=32+48-2=78$$
Задание 9
Найти значение выражения $$\frac{\log_{2}^{2}3}{\log_{2}12}-\frac{\log_{2}48*\log_{12}2}{\log_{48}2}$$
$$\frac{\log_{2}^{2}3}{\log_{2}12}-\frac{\log_{2}48*\log_{12}2}{\log_{48}2}=$$$$\frac{\log_{2}^{2}3}{\log_{2}12}-\frac{\log_{2}48*\log_{2}48}{\log_{2}12}=$$$$\frac{\log_{2}^{2}3-\log_{2}^{2}48}{\log_{2}12}=$$$$\frac{(\log_{2}3-\log_{2}48)*(\log_{2}3+\log_{2}48)}{\log_{2}12}=$$$$\frac{\log_{2}\frac{1}{16}*\log_{2}144}{\log_{2}12}=$$$$\frac{-4*2*\log_{2}12}{\log_{2}12}=-8$$
Задание 10
При температуре 0oС рельс имеет длину l0=10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t)=l_{0}(1+\alpha t^{0})$$ где $$\alpha=1,2*10^{-5}(^{0}C)^{-1}$$‐ коэффициент теплового расширения, t0‐ температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Представим миллиметры в метрах: 3 мм = 0,003 м. Подставим исходные данные в уравнение: $$10+0,003=10(1+1,2*10^{-5}*t)\Leftrightarrow$$$$10+0,003=10+1,2*10^{-4}t\Leftrightarrow$$$$t=\frac{0,003}{12*10^{-5}}=$$$$\frac{3*10^{-3}}{12*10^{-5}}=$$$$\frac{300}{12}=25$$
Задание 11
Лида спустилась по движущемуся эскалатору за 24 секунды. По неподвижному эскалатору с той же скоростью относительно него она спустится 42 секунды. За сколько секунд она спустится, стоя на ступеньках движущегося эскалатора?
Пусть x (частей эскалатора в секунду)-скорость Лиды , y –скорость эскалатора . Тогда , если эскалатор взять за 1:
$$\left\{\begin{matrix}\frac{1}{x+y}=24\\\frac{1}{x}=42\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}24x+24y=1\\x=\frac{1}{42}\end{matrix}\right.$$
$$24*\frac{1}{42}+y*24=1\Leftrightarrow$$$$24y=1-\frac{4}{7}=\frac{3}{7}\Leftrightarrow$$$$y=\frac{3}{7*24}=\frac{1}{56}$$
$$t_{y}=\frac{1}{\frac{1}{56}}=56$$ секунд
Задание 12
Найдите наименьшее значение выражения $$z=\sqrt{(2x-1)^{2}+(3y-1)^{2}}+\sqrt{(2x-3y)^{2}+9y^{2}}$$
Пусть $$\bar{a}: (2x-1; 3y-1);\bar{b}: (3y-2x ; -3y)$$
Из неравенства $$\left | \bar{a} \right |+\left | \bar{b} \right |\geq \left | \bar{a}+\bar{b} \right |$$, и учитывая , что $$\bar{a}+\bar{b}:(2x-1+3y-2x;3y-1-3y)=(3y-1;-1)$$, и $$z=\left | \bar{a} \right |+\left | \bar{b} \right |$$ получим : $$z\geq \left | \bar{a}+\bar{b} \right |=\sqrt{(3y-1)^{2}+(-1)^{2}}$$
Рассмотрим $$(3y-1)^{2}+(-1)^{2}=g$$ .Т.к. $$(3y-1)^{2}\geq 0$$ при любом y, $$g\rightarrow min$$, только тогда, когда $$3y-1\rightarrow 0$$, следовательно, $$g_{min}=1$$. Т.е. $$z\geq \sqrt{1}=1$$
Задание 13
ОДЗ: $$\cos 3x\neq 0\Leftrightarrow$$ $$3x\neq \frac{\pi}{2}+\pi n,n \in Z\Leftrightarrow$$$$x\neq \frac{\pi}{6}+\frac{\pi}{3}, n\in Z$$
Рассмотрим левую часть уравнения:
$$\sin^{2}2x+\sin ^{2}4x=$$$$\sin^{2}2x+ (2\sin 2x\cos 2x)^{2}=$$$$\sin^{2}2x(1+4\cos^{2}2x)=$$$$(1-\cos ^{2}2x)(1+4\cos ^{2}2x)=$$$$1+3\cos ^{2}2x-4 \cos^{4}2x$$
Подставим полученное выражение в уравнение:
$$1+3\cos^{2}2x-4\cos^{4}2x=1-\frac{\cos 2x}{\cos 3x}\Leftrightarrow$$$$4\cos ^{4}2x-3\cos ^{2}2x=\frac{\cos 2x}{\cos 3x}\Leftrightarrow$$$$\cos 2x(4\cos^{3}2x-3 \cos 2x)=\frac{\cos 2x}{\cos 3x}\Leftrightarrow$$$$\cos 2x*\cos 6x-\frac{\cos 2x}{\cos 3x}=0\Leftrightarrow$$$$\cos 2x(\cos 6x-\frac{1}{\cos 3x})=0$$
Произведение равно 0, когда хотя бы один из множителей равен 0:
$$\left[\begin{matrix}\cos 2x=0\\\cos 6x-\frac{1}{\cos 3x}=0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}2x=\frac{\pi}{2}+\pi n \Rightarrow x=\frac{\pi}{4}+\frac{\pi n }{2}\\(-1+2\cos^{2}3x)-\frac{1}{\cos 3x}=0(2)\end{matrix}\right.$$
Рассмотрим уравнение (2):$$2\cos ^{2}3x-1-\frac{1}{\cos 3x}=0$$, пусть $$\cos 3x=y$$, тогда: $$\frac{2y^{3}-y-1}{y}=0\Leftrightarrow$$$$(y-1)(2y^{2}+2y+1)=0$$. Так как вторая скобка всегда положительна, то: $$y=1\Leftrightarrow$$$$\cos 3x=1\Leftrightarrow 3x=2\pi n \Leftrightarrow x=\frac{2\pi n }{3}, n \in Z$$
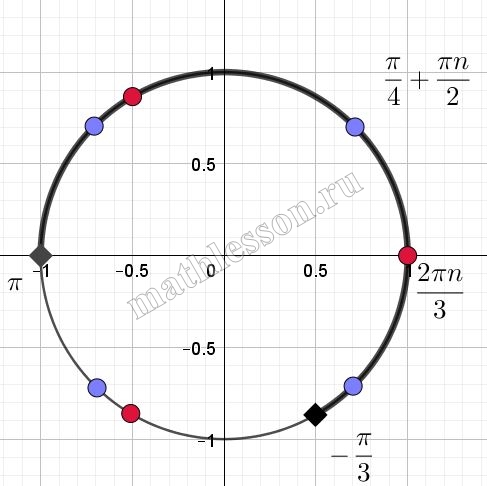
Б) Отметим полученные корни и промежуток на единичной окружности, найдем корни:
Для $$\frac{2\pi n}{3}$$ (красный цвет): $$0;\frac{2\pi}{3}$$
Для $$\frac{\pi}{4}+\frac{\pi n}{3}$$ (синий цвет): $$-\frac{\pi}{4};\frac{\pi}{4};\frac{3\pi}{4}$$
Задание 14
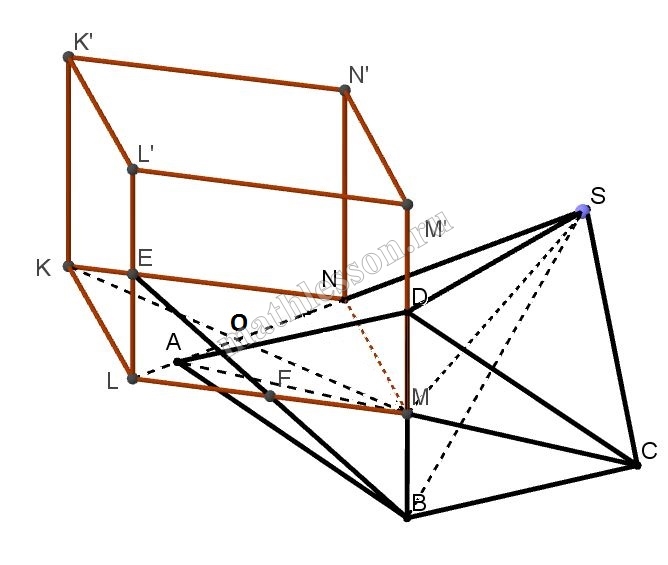
Основание прямой призмы KLMNK’L’M’N’ – ромб KLMN с углом 600 при вершине К. Точки Е и F – середины ребер LL’ и LM призмы. Ребро SA правильной четырехугольной пирамиды SABCD (S – вершина) лежит на прямой LN, вершины D и B – на прямых MM’ и EF соответственно. Известно, что SA=2AB.
А) 1) $$\left.\begin{matrix}LN\perp KM\\LN\perp LL_{1}\end{matrix}\right\}\Leftrightarrow$$ $$LN\perp MM_{1}K_{1}K\Rightarrow$$ $$SA\perp MM_{1}K_{1}K$$
2) т.к. BD-диагональ основания , то $$AS\perp BD$$ (в правильной четырехугольной пирамиде боковое ребро перпендикулярно скрещивающейся с ней диагональю основания ), $$\Rightarrow AS\perp MM_{1}K_{1}K AS\perp BD$$, то $$BD \in (MM_{1}K_{1}K)$$ или $$BD\left | \right |(MM_{1}K_{1}K)$$, но по условию $$BD\cap MM_{1}=D$$, следовательно, $$BD\in (MM_{1}K_{1}K)$$ и $$B \in MM_{1}$$
Б) 1) $$\Delta ELF=\Delta FMB$$($$LF=FM, \angle LEF=\angle MBF$$- накрест лежащие , $$\angle L=\angle M$$)$$\Rightarrow MB=EL=\frac{1}{2}LL_{1}=\frac{1}{2}MM_{1}$$
2) т.к. $$SA\perp ( MM_{1}K_{1}K)$$, то $$SA\perp KM$$ , но т.е. $$KM\perp BD$$, то, т.к. ABCD - квадрат, а диагонали квадрата перпендикулярны, то M-точка пересечения диагоналей . $$MO \perp SA$$
3) Пусть AB=a, тогда SA=2a, $$AM=MD=\frac{1}{2}BD=\frac{a\sqrt{2}}{2}$$
$$SM=\sqrt{SA^{2}-AM^{2}}=$$$$\sqrt{4a^{2}-\frac{a^{2}}{2}}=$$$$\frac{a\sqrt{14}}{2}$$
$$MO=\frac{AM*SM}{SA}=$$$$\frac{\frac{a\sqrt{2}}{2}*\frac{a\sqrt{14}}{2}}{2a}=$$$$\frac{a\sqrt{7}}{4}$$
$$LO=MO tg\angle LMO=MO*tg30=$$$$\frac{a\sqrt{7}}{4}*\frac{\sqrt{3}}{3}=$$$$\frac{a\sqrt{21}}{12}$$
$$S_{KMMN}=\frac{1}{2}KM*LN=$$$$\frac{1}{2}*2*MO*2*LO=$$$$2*\frac{a\sqrt{7}}{4}*\frac{a\sqrt{21}}{12}=$$$$\frac{7a^{2}\sqrt{3}}{24}$$
4) $$\Delta BMF=\Delta ELF\Rightarrow$$ $$EL=MB=MD=\frac{\sqrt{2}a}{2}\Rightarrow$$ $$LL_{1}=2EL=a\sqrt{2}$$, пусть $$V_{1}$$ и $$V_{2}$$ объемы $$KLMNK_{1}L_{1}M_{1}N_{1}$$ и $$SABCD$$, тогда:
$$V_{1}=S_{KLMN}*LL_{1}=$$$$\frac{7a^{2}\sqrt{3}}{24}*a\sqrt{2}=$$$$\frac{7a^{3}\sqrt{6}}{24}$$
$$V_{2}=\frac{1}{3}s_{ABCD}*SM=$$$$\frac{1}{3}a^{2}*\frac{a\sqrt{14}}{2}=$$$$\frac{a^{3}\sqrt{14}}{6}$$
$$\frac{V_{1}}{V_{2}}=\frac{7a^{3}\sqrt{6}}{24}*\frac{6}{a^{3}\sqrt{14}}$$$$=\frac{7\sqrt{6}}{4\sqrt{14}}=$$$$\frac{\sqrt{21}}{4}$$
Задание 15
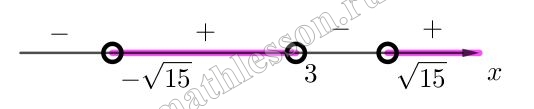
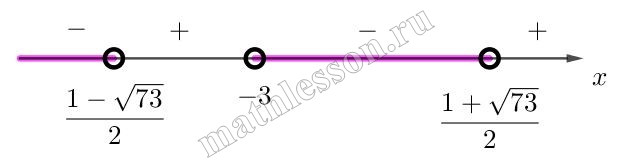
Решите неравенство $$\log_{\frac{1}{3}}\log_{2} \frac{x^{2}-|x|-12}{x+3}>0$$
ОДЗ : $$\left\{\begin{matrix}\log_{2}\frac{x-\left | x \right |-12}{x+3}>0(1)\\\frac{x^{2}-\left | x \right |-12}{x+3}>0(2)\end{matrix}\right.$$
(1): $$\frac{x^{2}-\left | x \right |-12}{x+3}>1\Leftrightarrow$$ $$\frac{(\left | x \right |+3)(\left | x \right |-4)-(x+3)}{x+3}>0$$
При $$x\geq 0:\frac{(x+3)(\left | x \right |-4-1)}{x+3}>0\Leftrightarrow$$ $$\left | x \right |-5>0\Leftrightarrow$$ $$x \in (-\infty; -5)\cup (5 ;+\infty )$$. С учетом $$x\geq 0: x\in (5;+\infty )$$
При $$x<0:\frac{x^{2}+x-12-x-3}{x+3}>0\Leftrightarrow$$ $$\frac{x^{2}-15}{x+3}>0$$.
С учетом $$x<0:x \in (-\sqrt{15}; -3)$$
(2): $$\frac{(\left | x \right |+3)(\left | x \right |-4)}{x+3}>0\Leftrightarrow$$ $$\frac{\left | x \right |-4}{x+3}>0\Leftrightarrow$$ $$\frac{(x-4)(x+4)}{x+3}>0$$
Итоговое ОДЗ:
$$x \in (-\sqrt{15} ;-3)\cup (5; +\infty )$$
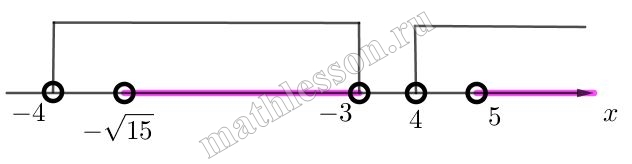
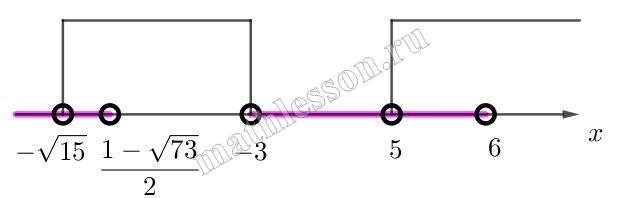
Решение:
$$\log_{2}\frac{(\left | x \right |+3)(\left | x \right |-4)}{x+3}<1\Leftrightarrow$$ $$\frac{(\left | x \right |+3)(\left | x \right |-4)}{x+3}<2\Leftrightarrow$$ $$\frac{(\left | x \right |+3)(\left | x \right |-4)-2(x+3)}{x+3}<0$$
При $$x\geq 0 : \frac{(x+3)(\left | x \right |-6)}{x+3}<0\Leftrightarrow$$ $$(x-6)(x+6)<0$$.С учетом $$x\geq 0: [0;6)$$
При $$x<0:\frac{x^{2}+x-12-2x-6}{x+3}<0 \Leftrightarrow$$ $$\frac{x^{2}-x-18}{x+3}<0$$
Рассмотрим числитель дроби: $$x^{2}-x-18=0$$, тогда $$D=1+72=73$$ и $$x_{1,2}=\frac{1\pm \sqrt{73}}{2}$$
C учетом $$x<0: (-\infty ;\frac{1-\sqrt{73}}{2})\cup (-3;0) $$
Итоговое решение $$x \in (-\infty ;\frac{1-\sqrt{73}}{2})\cup (-3; 6)$$
С учетом ОДЗ:
$$x \in (-\sqrt{15} ;\frac{1-\sqrt{73}}{2})\cup (5; 6)$$
Задание 16
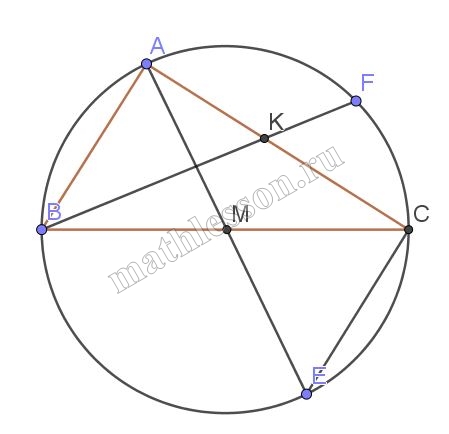
Продолжения медиан АМ и ВК треугольника АВС пересекают описанную около него окружность в точках Е и F соответственно, причем АЕ:АМ=2:1, BF:BK=3:2.
А) 1) $$AE:EM=2:1$$. Пусть $$ME=x\Rightarrow AE=2x$$, $$AM=x\Rightarrow$$ $$ME=AM$$, $$BM=MC$$(AM-медиана ), то по свойству хорд :
$$AM*ME=BM*MC\Leftrightarrow$$ $$AM^{2}=BM^{2}\Rightarrow$$ $$AM=BM(1)$$
2) из равенства 1 получаем , что $$\angle A=90\Rightarrow$$ BC-диаметр , AE-диаметр , тогда $$AM=BM=MC=ME$$, $$\angle AMB=\angle CME$$(вертикальные ) $$\Rightarrow\Delta AMB=\Delta CME$$ –равнобедренные $$\angle BAM=\angle MEC\Rightarrow$$ $$AB\left | \right |EC$$
Б) 1) Пусть $$AB=a, AC=b, BC=c, BK=m_{b}$$
2) По формуле длины медианы: $$BK=\frac{1}{2}\sqrt{2 AB^{2}+2BC^{2}-AC^{2}}\Leftrightarrow$$$$m_{b}=\frac{1}{2}\sqrt{2a^{2}+2 c^{2}-B^{2}}(1)$$
По свойству хорд : $$BK*KF=AK*KC$$. Т.к. $$BK:BF=\frac{2}{3}$$, то $$KF=\frac{1}{2}BK$$. Тогда получим: $$\frac{1}{2}m_{b}*m_{b}=\frac{b}{2}*\frac{b}{2}\Rightarrow$$ $$2m^{2}_{b}=b^{2}$$. Подставим в (1): $$4m^{2}_{b}=2a^{2}-b^{2}$$
$$2b^{2}+b^{2}=2a^{2}+2c^{2}\Leftrightarrow$$ $$3b^{2}=2a^{2}+2c^{2}$$
С другой стороны: $$a^{2}+b^{2}=c^{2}$$, тогда : $$\left\{\begin{matrix}2a^{2}-3b^{2}=-2c^{2}\\a^{2}+b^{2}=c^{2}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2a^{2}-3b^{2}=-2c^{2}\\2a^{2}+2b^{2}=2c^{2}\end{matrix}\right.\Leftrightarrow$$ $$4a^{2}-b^{2}=0\Leftrightarrow$$$$\frac{b^{2}}{a^{2}}=4\Leftrightarrow$$$$\frac{b}{a}=2=tg \angle B$$. Тогда $$\angle B=arctg 2, \angle C=90-arctg 2$$
Задание 17
На каждом из двух комбинатов работает по 1800 человек. На первом комбинате один рабочий изготавливает за смену 1 деталь А или 2 детали В. На втором комбинате для изготовления t деталей ( и А, и В) требуется t2 человеко‐смен. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна или 1 деталь А, или 1 деталь В. При этом комбинаты договариваются между собой изготавливать детали так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?
Так как для изготовления изделия нежна или 1 деталь А, или 1 деталь B( то есть они взаимозаменяемы) , тогда на первом комбинате всех рабочих эффективнее отправить на детали В . Их будет произведено $$1800*2=3600$$
На втором комбинате у рабочих пойдут на А , тогда 1800-y на B. При этом деталей A произведут $$\sqrt{y}$$ , деталей B: $$\sqrt{1800-y}$$
Из условия очевидно , что количество изделий соответствует общему количеству деталей: $$S=3600+\sqrt{y}+\sqrt{1800-y}$$. Найдем максимальное значение:
$${S}'=\frac{1}{2\sqrt{y}}+\frac{1}{2\sqrt{1800-y}}*(-1)=0$$
$$2\sqrt{y}=2\sqrt{1800-y}$$
$$y=1800-y\Rightarrow y=900$$ - точка максимума
Тогда максимальное количество изделий составит: $$S_{max}=S(900)=3600+\sqrt{900}+\sqrt{1800-900}=3660$$
Задание 18
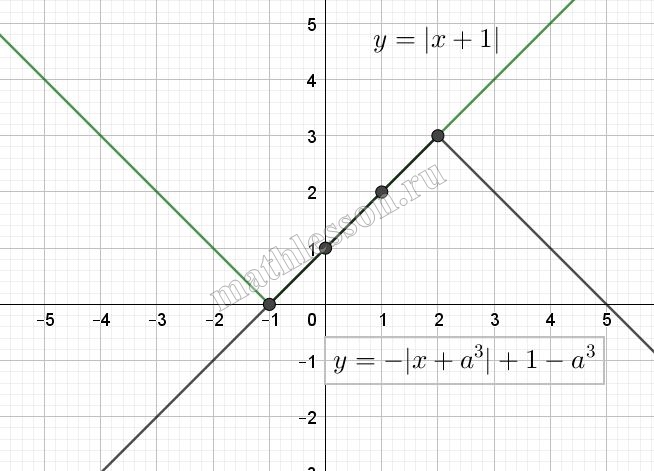
Найдите все значения параметра а, при которых уравнение $$a^{2}|a+\frac{x}{a^{2}}|+|x+1|=1-a^{3}$$ имеет не менее четырех различных решений, являющихся целыми числами?
Так как слева сумма модулей, то справа должно быть число неотрицательное :$$1-a^{3}\geq 0\Leftrightarrow$$ $$a^{3}\leq 1\Leftrightarrow$$ $$a\leq 1$$
Преобразуем уравнение :$$\left | x+1 \right |=-a^{2}\left | a+\frac{x}{a^{2}} \right |+(1-a^{3})$$
$$\left | a \right |^{2}=a^{2} \left | f \right |*\left | g \right |=\left | fg \right |$$
$$\left | x+1 \right |=-\left | a^{3}+x \right |+(1-a^{3})$$
$$f=\left | x+1 \right |$$ - график модуля смещённый на 1 по Ox влево.
$$f=-\left | a^{3}+x \right |+(1-a^{3})$$ - график $$\left | x \right |$$ смещённый на $$a^{3}$$ по Ox влево или право и $$1-a^{3}$$ по Oy вверх или низ и перевернуты (с учетом $$a\leq 1$$, то по Oy вверх и $$a^{3}$$ вправо от $$x=-1$$)
Начертим график функции:
Есть 2 случая удовлетворения условию задачи :
(1): $$\left\{\begin{matrix}-a^{3}\leq -4\\1-a^{3}\geq 3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a^{3}\geq 4\\a^{3}\leq -2\end{matrix}\right.\Leftrightarrow$$ $$\varnothing$$
(2):$$\left\{\begin{matrix}-a^{3}\geq 2\\1-a^{3}\geq 3\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a^{3}\leq -2\\a^{3}\leq -2\end{matrix}\right.\Leftrightarrow$$ $$a\leq \sqrt[3]{-2}]$$
Задание 19
При изучении темы «Среднее арифметическое» в классе из 34 учащихся раздали синие и красные карточки, при этом каждый из учеников получил хотя бы одну карточку, но не более одной каждого цвета. На каждой карточке написано одно целое число от 0 до 20 (на различных карточках могут быть записаны одинаковые числа). Среднее арифметическое по всем розданным карточкам оказалось равным 15 по каждому цвету в отдельности. Затем каждый ученик назвал наибольшее из чисел на своих карточках (если ему досталась одна карточка, то он назвал число, написанное на этой карточке). Среднее арифметическое всех названных чисел оказалось равно S.
A) Пусть у 30 человек и синие, и красные , но каждой из которых по 16 , у двух синие с О и у двух красных с О
Синие: $$\frac{30*16+2*0}{32}=15$$
Красные :$$\frac{30*16+2*0}{32}=15$$
Условие среднего арифметического выполняются : $$S=\frac{30*16+4*0}{34}<15\Rightarrow$$ да
Б) Пусть:
Так как средняя для синих и красных отдельно составляет 15, то и среднее для всех вообще чисел равно 15.
При этом всего было выдано $$34+k$$ карточек. Значит общая сумма $$15(34+k)=510+15k$$ . С другой стороны эту же сумму можно представить как $$a+b+c$$: $$a+b+c=510+15k(1)$$. При этом $$a+b=9*34=306$$ . Подставим в (1): $$306+c=510+15k\Leftrightarrow$$ $$c=204+15k$$
С другой стороны $$c\leq 20k$$ ( сумма наименьших будет максимальна если на всех карточках число 20)
Получаем: $$204+15k\leq 20k\Leftrightarrow$$ $$5k\geq 204\Leftrightarrow$$ $$k\geq 40,8$$ но $$k\leq 34$$, следовательно , нет.
B) Аналогично, $$a+b =34S, a+b+c=15(34+17)$$.Тогда $$34S+c=765\Rightarrow$$ $$S=\frac{765-c}{34}$$. Очевидно , что $$S\Rightarrow min$$, при $$c\Rightarrow max$$, т.е. $$S\geq \frac{765-17*20}{34}=12,5$$
Найдем такой пример :
У нас 17 человек с карточками красными и синими на каждой из которых по 20, тогда сумма на все оставшиеся карточки (по одной) составит :
$$765-2*340=85$$. При этом она приходится на 17 человек с одной карточкой . Пусть y-сумма на синих, тогда 85-y-на красных. Учитывая среднее 15 для синих и красных :
$$\left\{\begin{matrix}340+y=15(17+N)\\340+85-y=15(17+17-N)\end{matrix}\right.$$, Где N-число синих , тогда красных 17-N (речь идет об одиночных карточках)
$$\left\{\begin{matrix}\frac{340+y}{15}=17+N\\\frac{425-y}{15}=34-N\end{matrix}\right.$$
Слева должны быть натуральные числа, т.е. 340+y и 435-y делятся нацело на 15 . При y=20 получим :
$$\frac{340+20}{15}=\frac{360}{15}=24=17+N\Rightarrow N=7$$
$$\frac{425-20}{15}=27$$
Условия выполнились, следовательно , если у 17 человек синие и красные с числами 20, у 17 человек только синие с общей суммой 20( например 1+2+3+4+5+2+3) и у 10 только красных с суммой 65 (7+7+7+7+7+7+7+7+7+2), то S=12,5