318 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
Задание 1
В начале первой недели в пруд запустили 9 инфузорий. К концу каждой недели карась съедает 6 инфузорий, после чего каждая оставшаяся инфузория делится на 3 части. Сколько инфузорий будет в пруду в начале 31-й недели?
Задание 2
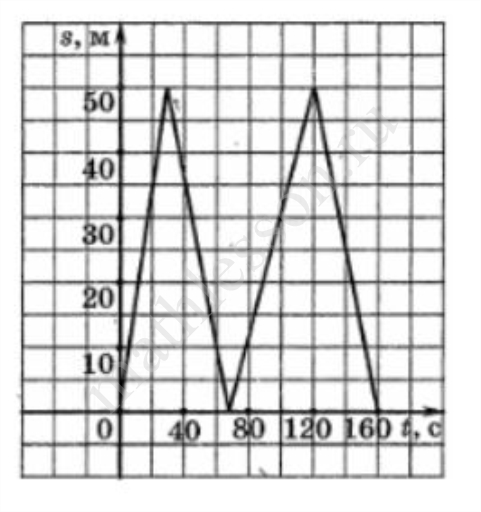
На тренировке в 50-метровом бассейне пловец проплыл 200-метровую дистанцию. На рисунке изображен график зависимости расстояния S (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца. Определите по графику, за какое время пловец преодолел первые 110 метров.
Задание 3
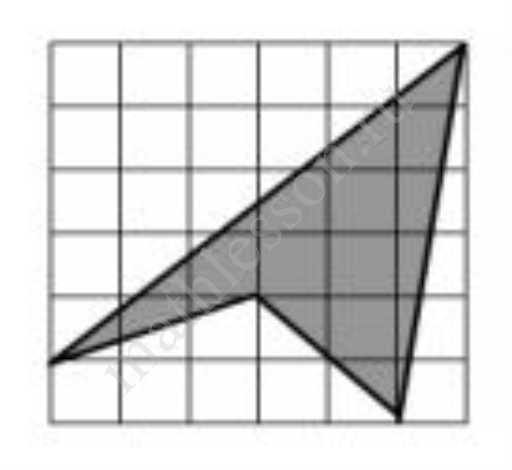
Из картонного листа размером 0,6 м $$\times$$ 0,6 м, изображенного на рисунке, нужно вырезать закрашенный четырехугольник. Найдите его массу (в граммах), если известно, что плотность картона равна $$160\frac{г}{м^2}$$
Задание 4
Лампы определенного типа выпускают только два завода. Среди продукции первого завода $$2\%$$ бракованных ламп, среди продукции второго - $$3\%$$. Известно, что при случайном выборе вероятность купить неисправную лампу этого типа равна 0,024. Найдите вероятность того, что случайно выбранная лампа произведена на первом заводе.
Задание 5
Найдите произведение всех различных корней уравнения: $${{\log }_3 x\ }-6\cdot {{\log }_x 9\ }=3$$
Задание 6
Длины диагоналей трапеции равны 9 и 12, а длина ее средней линии равна 7,5. Найдите площадь трапеции.

Пусть $$AF\parallel BD\ \to FC=AB+CD=7,5\cdot 2=15$$. Тогда $$\triangle FAC$$ - прямоугольный $$\left(9^2+{12}^2={15}^2\right)$$.
Пусть AH - высота $$\triangle FAC$$ (и ABCD) $$\to AH=\frac{9\cdot 12}{15}\to S_{ABCD}=\frac{15\cdot 9\cdot 12}{15\cdot 2}=\frac{108}{2}=54$$
Задание 7
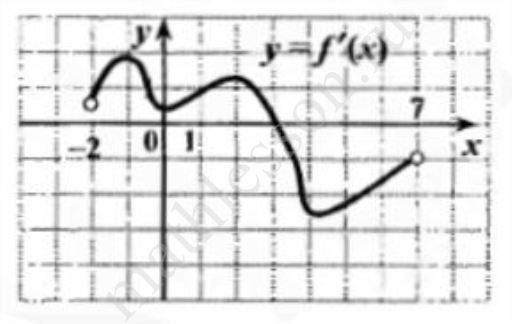
Функция $$y=f\left(x\right)$$ определена на промежутке $$\left(-2;7\right)$$. На рисунке изображен график ее производной. Найдите точку $$x_0$$, в которой функция $$f\left(x\right)$$ принимает наибольшее значение.
Задание 8
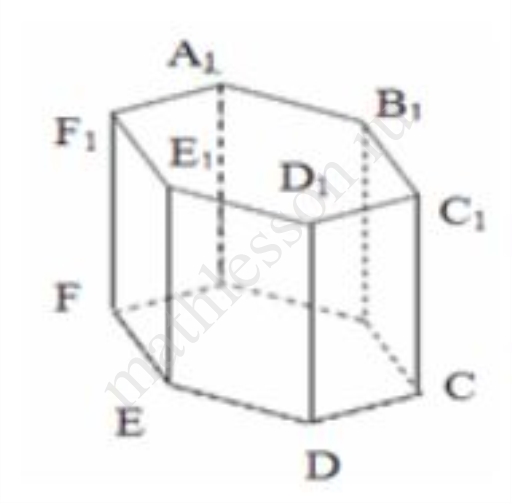
Найдите объем правильной шестиугольной призмы $$ABCDEFA_1B_1C_1D_1{E_1F}_1$$, если известно, что объем многогранника с вершинами в точках $$E,\ B_1,A_1,F_1,E_1$$ равен 12.
Задание 9
Найдите значение выражения $${{\log }_5 81\ }\cdot {{\log }_3 49\ }\cdot {{\log }_7 125\ }$$
Задание 10
Автомобиль, масса которого равна $$m=2400$$ кг, начинает двигаться с ускорением, которое в течение $$t$$ секунд остается неизменным, и проходит за это время путь $$S=480$$ метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно $$F=\frac{2\cdot m\cdot S}{t^2}$$. Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила $$F$$, приложенная к автомобилю, не меньше 4 кН. Ответ выразите в секундах.
Задание 11
Два велосипедиста с постоянными скоростями стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы. Через 10 минут после старта один из велосипедистов в первый раз догнал другого. Через какое время после старта первый велосипедист во второй раз догонит другого? Ответ дайте в минутах.
Задание 12
Найдите наименьшее значение функции $$y={{\log }_2 x\ }\cdot {{\log }_2 \left(16\cdot x\right)\ }+14$$
Задание 13
а) Решите уравнение $${{\log }_4 \left(2^{2x}-\sqrt{3}{\cos x\ }-{\sin 2x\ }\right)=x\ }$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$x\in \left[\pi ;;\frac{7\pi }{2}\right]$$
Задание 14
На боковом ребре $$SA$$ правильной треугольной пирамиды $$SABC$$ взята точка $$D$$, через которую проведено сечение пирамиды, пересекающее апофемы граней $$SAC$$ и $$SAB$$ в точках $$M$$ и $$N$$. Известно, что прямые $$DM$$ и $$DN$$ образуют углы $$\beta $$ с плоскостью основания пирамиды, а величины углов $$DMS$$ и $$DNS$$ равны $$\alpha $$, $$\left(\alpha <\frac{\pi }{2}\right)$$
а) Докажите, что секущая плоскость параллельна ребру $$BC$$
б) Найдите угол $$MDN$$, если $$\alpha =30{}^\circ ,\ \beta =45{}^\circ $$
Задание 16
Окружность с центром $$O$$, вписанная в прямоугольный треугольникa $$ABC$$, касается гипотенузы $$AB$$ в точке $$M$$, а катета $$AC$$ - в точке $$N$$, $$AC<BC$$. Прямые $$MN$$ и $$CO$$ пересекаются в точке $$K$$.
а) Докажите, что угол $$CKN$$ в два раза меньше угла $$ABC$$
б) Найдите $$BK$$, если $$BC=2\sqrt{2}$$
Задание 17
15 декабря планируется взять кредит в банке на 480 тысяч рублей на 27 месяцев.
Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на $$3\%$$ по сравнению с концом предыдущего месяца;
- со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
- 15-го числа первые два месяца и последний месяц долг должен уменьшиться на $$a$$ тысяч рублей, все остальные месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на $$b$$ тысяч рублей.
Найдите $$a$$, если всего было выплачено банку 656,4 тысяч рублей?
Задание 19
Имеется прямоугольная таблица размером $$M\times N$$, заполненная числами 0 и 1, обладающая следующими свойствами. Во-первых, в каждой строке и в каждом столбце есть хотя бы один элемент, равный 1. Во-вторых, нет ни одной пары одинаковых строк, а также ни одной пары одинаковых столбцов. Таблицы, обладающие этими свойствами, назовем «хорошими».
Две таблицы назовем эквивалентными в том (и только в том) случае, если из одной из них можно получить другую путем перестановки строк и/или столбцов. Приведем пример двух эквивалентных таблиц размером $$3\times 3$$.
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Вторая таблица получается из первой сначала перестановкой в ней 1-й и 3-й строк, потом 2-го и 3-го столбца в полученной таблице, а затем 1-й и 2-й строки в последней полученной таблице.
а) Сколько существует различных попарно неэквивалентных «хороших» таблиц размером $$2\times 3$$?
б) Укажите количество всех таблиц, эквивалентных «хорошей» таблице
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
в) Какое максимальное число столбцов может быть в «хорошей» таблице, содержащей М строк?