384 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.

Избавимся от знака модуля в левой части данного уравнения. Для этого рассмотрим три случая.

1) $$x\geq5.$$ В таком случае $$|5 - x| = x - 5, |x - 1| = x - 1$$ и исходное уравнение принимает вид: $$x - 5 + x - 1 = 10.$$

Решаем полученное уравнение: $$2x - 6 = 10; 2x = 10 + 6; 2x = 16; x = \frac{16}{2}; x = 8.$$ Поскольку $$8 > 5,$$ то данное значение $$x$$ является решением исходного уравнения.

2) $$1\leq x < 5.$$ В таком случае $$|5 - x| = 5 - x, |x - 1| = x - 1$$ и исходное уравнение принимает вид: $$5 - x + x - 1 = 10. 4 = 10.$$

Следовательно, при таких значениях $$x$$ исходное уравнение решений не имеет.

3) $$x < 1.$$ В таком случае $$|5 - x| = 5 - x, |x - 1| = 1 - x$$ и исходное уравнение принимает вид: $$5 - x + 1 - x = 10.$$

Решаем полученное уравнение: $$6 - 2x = 10; 2x = 6 - 10; 2x = -4; x = -\frac{4}{2}; x = -2.$$ Поскольку $$-2 < 1,$$ то данное значение $$x$$ является решением исходного уравнения.

Данное уравнение имеет два решения: $$x = 8$$ и $$x = -2.$$

$$8+(-2)=6$$

Если выпало сначала 1 (вероятность $$\frac{1}{6}$$), то потом должно выпасть от 4 до 6 (вероятность $$\frac{3}{6}$$).

Если 2 $$(\frac{1}{6}),$$ то от 3 до 6 $$(\frac{4}{6});$$ если 3 $$(\frac{1}{6}),$$ то от 2 до 6 $$(\frac{5}{6});$$ если 4 $$(\frac{1}{6}),$$ то любое.

Получим:

$$P(A)=\frac{1}{6}\cdot\frac{3}{6}+\frac{1}{6}\cdot\frac{4}{6}+\frac{1}{6}\cdot\frac{5}{6}+\frac{1}{6}\cdot1=\frac{3+4+5+6}{36}=0,5$$

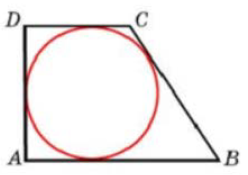
Из рисунка видно, что радиус окружности равен половине стороны AD. Найдем длину стороны AD из условия равенства суммы противоположных сторон в четырехугольнике, описанном вокруг окружности:

$$AD+BC=AB+DC=\frac{P}{2}=11,$$

откуда

$$AD=11-BC=11-7=4,$$

и радиус вписанной окружности, равен:

$$r=\frac{AD}{2}=\frac{4}{2}=2.$$

$$3^{\log_{\sqrt[4]{3}}5}=3^{\log_{3^{0,25}}5}=3^{\frac{1}{0,25}\cdot\log_3 5}=3^{\log_3 5^4}=5^4=625$$

$$2^{\log_8 26^3}=2^{\frac{1}{3}\log_2 26^3}=2^{\log_2 (26^3)^{\frac{1}{3}}}=26$$

$$4^{4\log_{16}5}=4^{4\cdot\frac{1}{2}\log_4 5}=4^{\log_4 5^2}=25$$

$$\frac{625-26-10}{25-6}=31$$

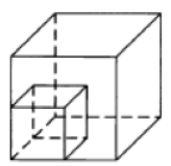
Если принять за начальную длину ребра куба значение $$a,$$ то исходная площадь поверхности куба, составленная из сумм площадей всех 6 его граней, равна $$S=6a^2.$$ После того, как ребро увеличили в 15 раз, оно стало равным $$15a$$ и площадь поверхности стала равной

$$S_2=6\cdot(15a)^2=6\cdot225a^2$$.

Таким образом, площадь поверхности увеличилась в

$$\frac{S_2}{S}=\frac{6\cdot225a^2}{6a^2}=225$$ раз.

На графике производной точка минимума - пересечение оси Ox при возрастании производной: $$-19;-12;2.$$

На $$[-20;-1]$$ лежит 2 из них.

$$R=\frac{2In+Op+3Tr+Q}{A}.$$

$$0,5=\frac{2\cdot5+5+3\cdot5+5}{A}=\frac{35}{A},$$

откуда

$$A=\frac{35}{0,5}=70.$$

Пусть первая печатает $$x$$ страниц в единицу времени, вторая $$y$$ страниц. Всего в рукописи $$S$$ страниц. Получим:

$$\left\{\begin{matrix} \frac{S-80}{x}=\frac{80}{y}\\ \frac{80}{x}=\frac{S-80-36}{y} \end{matrix}\right.$$

Поделим первое уравнение на второе:

$$\frac{S-80}{x}:\frac{80}{x}=\frac{80}{y}:\frac{S-116}{y}\Leftrightarrow\frac{S-80}{80}=\frac{80}{S-116}\Leftrightarrow$$

$$\Leftrightarrow(S-80)(S-116)=80^2\Leftrightarrow S^2-196S+9280-6400=0\Leftrightarrow$$

$$\Leftrightarrow S^2-196S+2880=0$$

$$\frac{D}{4}=98^2-2880=6724=82^2$$

$$S_1=\frac{98+82}{1}=180$$

$$S_2=\frac{98-82}{1}=16<80$$

График проходит через $$(-1;-1); (-2;0)$$ и $$(-4;-4).$$

Получим:

$$\left\{\begin{matrix} -1=\frac{a\cdot(-1)+b}{-1+c}\\ 0=\frac{a\cdot(-2)+b}{-2+c}\\ -4=\frac{a\cdot(-4)+b}{-4+c} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -1=\frac{b-a}{c-1}\\ 0=\frac{b-2a}{c-2}\\ -4=\frac{b-4a}{c-4} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1-c=b-a\\ b-2a=0\\ 16-4c=b-4a \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1-c=2a-a\\ b=2a\\ 16-4c-b=-4a \end{matrix}\right.\Leftrightarrow$$

$$\Leftrightarrow\left\{\begin{matrix} c=1-a\\ b=2a\\ 16-4+4a-2a=-4a \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=-2\\ b=-4\\ c=3 \end{matrix}\right.$$

Получим:

$$y=\frac{-2x-4}{x+3}.$$

$$y(17)=\frac{-34-4}{17+3}=\frac{-38}{20}=-1,9$$

$$990+6+3+1=1000$$ - всего билетов

$$\frac{990}{1000}=0,99$$ - шанс купить билет с выигрышем 10 руб.

$$0,006;0,003;0,001$$ - остальные билеты

$$990\cdot0,99+6\cdot0,006+3\cdot0,003+0,001=15,5$$ - математическое ожидание

$$50-15,5=34,5$$

$$y=x^2\cdot e^x\Rightarrow y'=(x^2)'e^x+(e^x)'x^2=2xe^x+e^xx^2=e^xx(2+x)=0$$

$$\left[\begin{matrix} x=0\\ 2+x=0 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} x=0\\ x=-2 \end{matrix}\right.$$

$$y'(-3)=e^{-3}\cdot(-3)(2-3)>0$$

$$y'(-1)=e^{-1}\cdot(-1)(2-1)<0$$

$$y'(1)=e^{1}\cdot1\cdot(2+1)>0$$

Тогда $$x=-2$$ - точка максимума