281 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.
Решаем ЕГЭ 281 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12 заданий тренировочного варианта ЕГЭ Ларина №281 (alexlarin.com)
Решаем ЕГЭ 281 вариант Ларина. Подробное решение 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №281 (alexlarin.com)
Задание 1
Каждый преподаватель за одну лекцию расходует 1,5 куска мела. На кафедре работают 9 преподавателей и каждый из них читает 3 лекции в день. На какое максимальное количество дней хватит мела, если на кафедру принесли коробку с 200 кусками?
Найдем количество мелков, которое расходуется на кафедре в день: 1,5*9*3=40,5
Тогда 200 мелков хватит на $$\frac{200}{40,5}<5$$ дней, то есть максимум на 4 дня
Задание 2
На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 10 по 26 ноября 2008 г. По горизонтали указываются числа месяца, по вертикали – цена тонны никеля (в долларах США). Для наглядности жирные точки на рисунке соединены линией. 13 ноября бизнесмен купил 100 т никеля, а 21 ноября продал их. Найдите убыток бизнесмена от этой сделки (в долларах США)
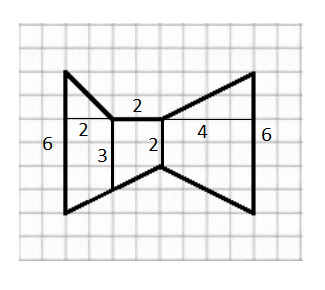
Задание 3
Разобьем фигуру на трапеции, как показано на рисунке, и проведем в каждой высоту. Тогда площадь данной фигуры равна сумме площадей трапеций: $$S=\frac{6+3}{2}*2+\frac{3+2}{2}*2+\frac{2+6}{2}*4=30$$
Задание 4
Взяв пассажира в аэропорт, таксист Рушан быстро прикинул в уме, что при текущей загруженности маршрута вероятность успеть к началу регистрации на рейс равна 0,9, если ехать без остановок. Однако на пути в аэропорт есть пост ГИБДД, на котором Рушана могут остановить для проверки документов с вероятностью 0,5. В таком случае вероятность успеть вовремя будет равна 0,7. Какова вероятность успеть к началу регистрации при поездке по этому маршруту?
Вероятность, что таксиста остановят, составляет 0,5, следовательно, вероятность того, что не остановят (противоположное событие) : 1-0,5=0,5
Успеть он может в двух случаях:
- его остановили и он успел: 0,5*0,7=0,35
- его не остановили и он успел: 0,5*0,9=0,45
Тогда вероятность успеть в аэропорт: 0,35+0,45=0,8
Задание 5
Задание 6
В треугольнике АВС стороны АВ=12, ВС=13, $$\angle ABC=\pi-arccos \frac{5}{13}$$ . Найдите площадь треугольника АВС.
Задание 7
На рисунке изображен график $$y=f'(x)$$ ‐ производной функции $$f(x)$$, определенной на интервале (-12;9). Найдите количество точек максимума функции $$f(x)$$, принадлежащих отрезку [-9;8]
Задание 8
В аквариум кубической формы с ребром 50 см, наполовину заполненный водой, брошена стальная деталь цилиндрической формы с радиусом основания $$\frac{5}{\pi}$$ см и высотой 10 см. На сколько сантиметров поднялся уровень воды в аквариуме?
Задание 9
Задание 10
Абсолютный показатель преломления среды для прохождения света может быть вычислен по формуле $$n=\frac{c}{\upsilon}$$, где $$c=3\cdot 10^{8}$$ м/с – скорость света в вакууме, c ‐ скорость света в среде в м/с. Стоя на светофоре, таксист Рушан захотел посчитать коэффициент преломления для красного света. Приняв длину волны красного света $$\lambda=6\cdot 10^{-7}$$ м, а энергию фотона $$E=4,42*10^{-19}$$ Дж∙с, Рушан воспользовался формулой Планка $$E=\frac{h\upsilon}{\lambda}$$ , приняв постоянную Планка h равной $$6,63*10^{-34}$$ Дж. Какой коэффициент преломления получил Рушан?
Задание 11
Скорость первого бегуна на 4 км/ч больше скорости второго, а 1 км первый бегун преодолевает на 30 секунд быстрее, чем второй. За какое время (в секундах) первый бегун пробежит 800 м?
Задание 12
Найдите наименьшее значение функции $$y=3-\sqrt{96-x^{2}-4x}$$ на отрезке $$[-5;8]$$
Задание 13
A) $$4^{\cos 2x}-\frac{1}{2}\cdot 16^{\sin^{2}x}=1$$ $$\Leftrightarrow$$ $$4^{1-2\sin^{2}x}-\frac{1}{2}(4^{2})^{\sin^{2}x}=1$$ $$\Rightarrow$$ $$4^{\frac{4}{2\sin^{2}x}}-\frac{1}{2}\cdot4^{2\sin^{2}x}=1$$. Замена: $$4^{2\sin^{2}x}=y>0$$
Решение: $$\frac{4}{y}-\frac{y}{2}=1$$ $$\Leftrightarrow$$ $$\frac{8-y^{2}-2y}{2y}=0|\cdot(-2y)$$ $$\Leftrightarrow$$ $$y^{2}+2y-8=0$$ $$\Leftrightarrow$$ $$\begin{bmatrix}y_{1}+y_{2}=-2&\\y_{1}\cdot y_{2}=-8&\end{bmatrix}$$ $$\Leftrightarrow$$ $$\begin{bmatrix}y_{1}=-4<0&\\y_{2}=2&\end{bmatrix}$$
Обратная замена: $$4^{2\sin^{2}x}=2$$ $$\Leftrightarrow$$ $$2^{4\sin^{2}x}=2$$ $$\Leftrightarrow$$ $$\sin^{2}x=\frac{1}{4}$$ $$\Leftrightarrow$$ $$\sin x=\pm\frac{1}{2}$$ $$\Leftrightarrow$$ $$x=\pm\frac{\pi}{6}+\pi k,k\in Z$$
Б) Отметим на единичной окружности полученные корни и найдем их значения на $$[0;\frac{3\pi}{2}]$$:
1) $$0+\frac{\pi}{6}=\frac{\pi}{6}$$;
2) $$\pi-\frac{\pi}{6}=\frac{5\pi}{6}$$;
3) $$\pi+\frac{\pi}{6}=\frac{7\pi}{6}$$;
Задание 14
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 ребро основания АВ=2, высота АА1=6, точка М – середина F1E1, проведено сечение через точки А, С и М.
A) 1) Построим сечение: через $$M$$ проведем прямую $$a\parallel AC$$; $$a\cap E_{1}D_{1}=N$$ $$\Rightarrow$$ $$MN\parallel AC$$.
$$MN\cap C_{1}D_{1}=O_{2}$$; $$MN\cap A_{1}F_{1}=O_{1}$$; $$CO_{2}=\cap DD_{1}=K$$; $$AO_{1}\cap FF_{1}=L$$ $$\Rightarrow$$ $$(ACKNML)$$ - сечение
2) $$A_{1}C_{1}\parallel AC$$; $$AC\parallel MN$$ $$\Rightarrow$$ $$A_{1}C_{1}\parallel MN$$; $$F_{1}D_{1}\parallel MN$$ $$\Rightarrow$$ $$\bigtriangleup F_{1}E_{1}D_{1}\sim\bigtriangleup ME_{1}N$$ $$\Rightarrow$$ $$\frac{F_{1}N}{ME_{1}}=\frac{D_{1}N}{NE_{1}}=\frac{1}{1}$$
Б) 1) Опустим из $$R$$ перпендикуляр $$PR'$$ на $$(ABC)$$. Из $$\bigtriangleup HBC$$: $$\angle C=30^{\circ}$$ $$\Rightarrow$$ $$HB=\frac{BC}{2}=1$$; $$HC=\sqrt{3}$$; $$ER'=\frac{HB}{2}=0,5$$. $$EB=2AB=4$$ $$\Rightarrow$$ $$R'H=4-1-0,5=2,5$$
2) Из $$\bigtriangleup RR'H$$: $$RR'=DD_{1}=6$$ $$\Rightarrow$$ по т. Пифагора: $$RH=\sqrt{6^{2}+2,5^{2}}=6,5=CO_{2}$$
3) $$S_{ACKNML}=S=S_{CO_{2}O_{1}A}-2S_{NO_{2}K}$$ (т.к. $$\bigtriangleup NO_{2}K=\bigtriangleup MO_{1}L$$ по катету $$NO_{2}=MO_{1}$$ и острому углу $$\angle N=\angle M$$)
4) $$NO_{2}=RN=\frac{1}{2}HC=\frac{\sqrt{3}}{2}$$; $$O_{2}D_{1}=E_{1}R=\frac{1}{2}$$ $$\bigtriangleup O_{2}D_{1}K\sim\bigtriangleup DKC$$ $$\Rightarrow$$ $$\frac{D_{1}K}{KD}=\frac{O_{2}D_{1}}{DC}=\frac{\frac{1}{2}}{2}=\frac{1}{4}$$ $$\Rightarrow$$ $$D_{1}K=\frac{DD_{1}}{5}=\frac{6}{5}$$
Из $$\bigtriangleup O_{2}DK$$: $$O_{2}K=\sqrt{(\frac{1}{2})^{2}+(\frac{6}{5})^{2}}=\frac{13}{10}$$
Из $$\bigtriangleup NO_{2}K$$: $$S_{NO_{2}K}=\frac{1}{2}\cdot\frac{13}{10}\cdot\frac{\sqrt{3}}{2}=\frac{13\sqrt{3}}{40}$$
5) $$AC=2HC=2\sqrt{3}$$ $$\Rightarrow$$ $$S=2\sqrt{3}\cdot6,5-\frac{13\sqrt{3}}{40}\cdot2=\frac{247\sqrt{3}}{20}$$
Задание 15
Решите неравенство: $$\frac{4\sin x \cdot \sin 2x -\sin^{2} 2x -4+4\cos^{2} x}{\sqrt{16-2^{(x-5)^{2}}}}\geq 0$$
ОДЗ: $$16-2^{(x-5)^{2}}>0$$ $$\Leftrightarrow$$ $$2^{4}>2^{(x-5)^{2}}$$ $$\Leftrightarrow$$ $$4>(x-5)^{2}$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x-5<2&\\x-5>-2&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x<7&\\x>3&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$x\in(3;7)$$
Упростим числитель: $$4\sin x\sin2x-\sin^{2}2x+4(\cos{2}x-1)=8\sin^{2}x\cos x-4\sin^{2}x$$
$$\cos^{2}x-4\sin^{2}x=-4\sin^{2}x(\cos^{2}-2\cos x+1)=-4\sin^{2}x(\cos^{2}-1)^{2}$$
Тогда получим: $$-\frac{4\sin^{2}x(\cos x-1)^{2}}{\sqrt{16-2^{(x-5)^{2}}}}\geq0$$ $$\Leftrightarrow$$ $$\sin^{2}x(\cos x-1)^{2}\leq0$$ $$\Leftrightarrow$$ $$\begin{bmatrix}sin x=0&\\\cos x=1&\end{bmatrix}$$ $$\Leftrightarrow$$ $$x=\pi n,n\in Z$$
С учетом ОДЗ: $$\left\{\begin{matrix}x=\pi n &\\x\in(3;7)&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$x=\pi;2\pi$$
Задание 16
В трапеции ABCD отношение оснований $$\frac{AD}{BC}=\frac{5}{2}$$. Точка М лежит на АВ, площадь трапеции ABCD равна 20.
А) 1) Пусть $$BC=2x$$, тогда $$AD=5x$$; $$MN=y\cdot k$$; $$NH\perp BC$$ и $$NH\pepr AD$$ $$\Rightarrow$$ $$\bigtriangleup NBM\sim\bigtriangleup AMH$$. Пусть $$\frac{BM}{MA}=k$$ $$\Rightarrow$$ $$MH=y$$. Пусть $$NH=h=y(k+1)$$
2) $$S_{ABCD}=\frac{2x+5x}{2}\cdot y(k+1)=3,5xy(k+1)=20=3/5xh$$
$$S_{BCM}=\frac{1}{2}2x\cdot ky=xky$$. $$S_{AMD}=\frac{1}{2}5x\cdot y=2,5xy$$
Тогда $$S_{CMD}=3,5xy(k+1)-xky-2,5xy=2,5kxy+xy=1,5kxy+xy(k+1)=1,5kxy+\frac{20}{3,5}$$
3) Учтем, что $$xky\rightarrow max$$, когда $$ky=h$$ $$\Rightarrow$$ $$max(S_{BCM})=xh=\frac{20}{3,5}$$ $$\Rightarrow$$ $$max(S_{CMD})=\frac{1,5\cdot20}{3,5}+\frac{20}{3,5}=\frac{50}{3,5}=\frac{100}{7}<1,5$$
Б) 1) $$S_{MCD}=9$$ $$\Rightarrow$$ $$S_{MBC}+S_{AMD}=11$$ $$\Rightarrow$$ $$\left\{\begin{matrix}xky+2,5xy=11&\\3,5xy(k+1)=20&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}xy(k+2,5)=11(1)&\\xy(3,5k+3,5)=20(2)&\end{matrix}\right.$$
Поделим $$(1)$$ на $$(2)$$: $$\frac{k+2,5}{3,5k+3,5}=\frac{11}{20}$$ $$\Leftrightarrow$$ $$20k+50=38,5k+38,5$$
$$18,5k=11,5$$ $$\Rightarrow$$ $$k=\frac{11,5}{18,5}=\frac{23}{37}=\frac{MB}{AM}$$ $$\Rightarrow$$ $$\frac{AM}{MB}=\frac{37}{23}$$
Задание 17
Клиент оформил ипотеку в банке на 1 000 000 рублей 1 июля 2019 года на 3 года. Начиная с 1 августа 2019 года он должен выплачивать ежемесячно одну и ту же сумму. 15 июля 2019 года сумма долга увеличивается на 10%, 15 июля 2020 года – на 20%, а 15 июля 2021 года – на 30%. Найти сумму ежемесячной платы. Ответ округлите до 1 руб в большую сторону.
Пусть $$S=10^{6}$$; $$n=3$$ года, $$x$$ - месячная выплата $$\Rightarrow$$ $$12x$$ - годовая. Распишем таблицу:
| Год | Долг на начало | Начисленный процент | Выплата |
| 2019 | $$S$$ | $$0,1S$$ | $$12x$$ |
| 2020 | $$1,1S-12x$$ | $$0,2(1,1S-12x)$$ | $$12x$$ |
| 2021 | $$((1,1S-12x)1,2-12x)$$ | $$0,3((1,1S-12x)1,2-12x)$$ | $$12x$$ |
Получим: $$((1,1S-12x)1,2-12x)1,3-12x=0$$ $$\Leftrightarrow$$ $$\frac{11\cdot12\cdot13}{10^{3}}S-\frac{12\cdot12\cdot13x}{10^{2}}-\frac{12\cdot13x}{10}-12x=0|\cdot10^{3}$$ $$\Leftrightarrow$$ $$11\cdot12\cdot13S-12^{2}\cdot13\cdot10x-12\cdot13\cdot10^{2}x-12\cdot10^{3}x=0$$ $$\Leftrightarrow$$ $$x=\frac{11\cdot12\cdot13S}{10(156+130+100)}=\frac{11\cdot12\cdot13\cdot10^{6}}{10\cdot386}\approx37047$$
Задание 18
При каких значениях параметра a уравнение $$6\cdot (\frac{x}{x^{2}+1})^{2}-\frac{(6a+1)x}{x^{2}+1}-12a^{2}+8a-1=0$$ имеет ровно 4 решения?
Пусть $$(\frac{x}{x^{2}+1})=y$$. Получим: $$6y^{2}-(6a+1)\cdot y-(12a^{2}-8a+1)=0$$
Данное уравнение должно иметь 2 различных корня, неравных 0 (иначе при обратной замене, не получим 4 корня):
$$D=(6a+1)^{2}+24(12a^{2}-8a+1)>0$$ $$\Rightarrow$$ $$324a^{2}-180a+25>0$$ $$\Rightarrow$$ $$(18a-5)^{2}>0$$ $$\Rightarrow$$ $$a\neq\frac{5}{18}$$
$$\begin{bmatrix}y_{1}=\frac{6a+1+18a-5}{12}&\\y_{2}=\frac{6a+1-18a+5}{12}&\end{bmatrix}$$ $$\Leftrightarrow$$ $$\begin{bmatrix}y_{1}=\frac{6a-1}{3}&\\y_{2}=\frac{1-2a}{2}&\end{bmatrix}$$
При этом $$\frac{6a-1}{3}\neq0$$ $$\Rightarrow$$ $$a\neq\frac{1}{6}$$ и $$\frac{1-2a}{2}\neq0$$ $$\Rightarrow$$ $$a\neq\frac{1}{2}$$
При этом $$\frac{x}{x^{2}+1}=y$$ так же имеет два различных корня: $$yx^{2}=0$$ $$D=1-4y^{2}>0$$ $$\Rightarrow$$ $$y\in(-\frac{1}{2};\frac{1}{2})$$
То есть: $$\left\{\begin{matrix}-\frac{1}{2}<\frac{6a-1}{3}<\frac{1}{2}|\cdot3|+1|\div6&\\-\frac{1}{2}<\frac{1-2a}{2}<\frac{1}{2}|\cdot2|-1|\div(-2)&\\a\neq\frac{5}{18};\frac{1}{6};\frac{1}{2}&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}-\frac{1}{12}<a<\frac{5}{12}&\\0<a<1&\\a\neq\frac{5}{18};\frac{1}{6};\frac{1}{2}&\end{matrix}\right.$$ $$\Leftrightarrow$$ $$a\in(0;\frac{1}{6})\cup(\frac{1}{6};\frac{5}{18})\cup(\frac{5}{18};\frac{5}{12})$$
Задание 19
Известно, что уравнение $$x^{3}-3x^{2}+bx+12=0$$ имеет три различных целых корня.
Пусть $$c,d,e$$ - корни данного уравнения. Тогда получим: $$(x-c)(x-d)(x-e)=0$$ $$\Leftrightarrow$$ $$(x^{2}-xc-xd+cd)(x-e)=0$$ $$\Leftrightarrow$$ $$x^{3}-x^{2}e-x^{2}(c+d)+xe(c+d)+cdx-cde=0$$ $$\Leftrightarrow$$ $$x^{3}-x^{2}(c+d+e)+x(ce+de+cd)-cde=0$$
Получим, что $$c+d+e=-3$$; $$ce+ed+cd=b$$; $$-cde=12$$
А) Т.к. $$-cde=12$$. Т.е. $$-cde=2\cdot2\cdot3$$. Т.е. один точно будет нечетным $$\Rightarrow$$ нет
Б) $$-cde=12$$ тогда или 1 или 3 отрицательных. Но 3 не может быть, т.к. $$c+d+e=-3$$ выполнялось бы только при $$c=d=e=-1$$ (т.е. $$c,d,e,\in Z$$), но тогда они не различны и не дают $$-cde=12$$ $$\Rightarrow$$ один отрицательный
В) Рассмотрим возможные комбинации корней $$12=1\cdot2\cdot6=1\cdot3\cdot4=2\cdot2\cdot3=1\cdot1\cdot12$$. Учтем, что один корень отрицательный (иначе $$2\cdot2\cdot3$$ и $$1\cdot1\cdot12$$ не рассматривали бы): имеем $$(x-c)(x-d)(x-e)=0$$ $$\Leftrightarrow$$ $$x^{3}+x^{2}(e-c-d)+x(cd-ec-ed)+abc=0$$
При этом $$e-c-d=-3$$
1) $$6-2-1\neq-3$$; $$2-6-1\neq-3$$; $$1-2-6\neq-3$$
3) $$4-1-3\neq-3$$; $$1-4-3\neq-3$$; $$3-1-4\neq-3$$
3) $$2-2-3=-3$$; $$3-2-2\neq-3$$
4) $$12-1-1\neq-3$$; $$1-12-1\neq-3$$