325 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

Решаем ЕГЭ 325 вариант Ларина ЕГЭ 2021 по математике. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №325 (alexlarin.com)

Аналоги к этому заданию:

Задание 1

В 14-этажном доме расположены 336 квартир по 4 квартиры на этаже. Между этажами по два лестничных пролета, по 11 ступенек каждый. Лифты сломались, а старший по дому обходит квартиры в порядке возрастания номеров (начиная с первой). Прохождение каждых 50 ступенек обходится ему появлением новой мозоли. Сколько мозолей он заработал за вечер, обойдя 170 квартир и выйдя из дома (ступеньки для входа на первый этаж не считаются)?

Ответ: 34

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть $$\frac{170}{4}=42,5$$ этажей вверх надо пройти $$\to \frac{42,5}{14}=3\frac{1}{28}$$ подъезда. Т.е. 3 раза он поднимется на 14 этаж и спустится обратно. Количество пролетов в 3-х подъездах: $$2\cdot 13\cdot 3=78$$ пролетов $$\to 78\cdot 11=858$$ ступенек, т.е. $$858\cdot 2=1716$$ ступенек пройдет. Оставшиеся квартиры на первом этаже 4-го подъезда, их несчитаем. Тогда $$\frac{1716}{50}=34,32\to $$ 34 мозоли.

Аналоги к этому заданию:

Задание 2

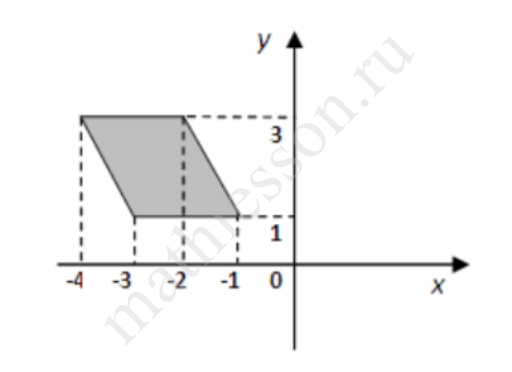
На диаграмме показана среднемесячная температура воздуха в Новосибирске за каждый месяц 1892 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме, какой была средняя температура (в градусах Цельсия) в самом прохладном летнем месяце.

Ответ: 15

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть Самый холодный месяц - август (8). Температура составляет 15.

Аналоги к этому заданию:

Задание 3

Найдите площадь закрашенного четырехугольника.

Ответ: 4

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть Дан параллелограмм: $$S=ah=\left(-1-\left(-3\right)\right)\cdot \left(3-1\right)=2\cdot 2=4$$.

Аналоги к этому заданию:

Задание 4

При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем - 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?

Ответ: 5

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть Вероятность не уничтожения цели тогда менее $$\left(1-0,98\right)=0,02.$$ Промах при первом выстреле: $$1-0,4=0,6.$$ Далее $$1-0,6=0,4.$$ Тогда через n выстрелов вероятность не уничтожения:

$$0,6\cdot {0,4}^{n-1}<0,02\to {0,4}^n<\frac{0,02\cdot 0,4}{0,6}\approx 0,01\to n=5$$

$$({0,4}^5=0,01204<0,01(3))$$

Аналоги к этому заданию:

Задание 5

Решите уравнение $${\left(x+3\right)}^2={\left(x+3\right)}^4$$. В ответе укажите меньший корень.

Ответ: -4

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

$${\left(x+3\right)}^2={\left(x+3\right)}^4;\ $$пусть $${\left(x+3\right)}^2=y\ge 0:$$

<div class="respons-table-block">$$y=y^2\to y\left(y-1\right)=0\leftrightarrow \left[ \begin{array}{c} {\left(x+3\right)}^2=0 \\ {\left(x+3\right)}^2=1 \end{array} \right.\leftrightarrow \left[ \begin{array}{c} x=-3 \\ x=-2 \\ x=-4 \end{array} \right.\to $$</div>

Ответ: -4

Аналоги к этому заданию:

Задание 6

Равнобокая трапеция АВСD разбивается диагональю АС на два равнобедренных треугольника. Определите, чему равен больший угол трапеции. Ответ дайте в градусах.

Ответ: 108

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть $$\triangle ABC$$ - равнобедренный, $$AB=BC\to \angle BAC=\angle BCA=\alpha ;$$ $$\angle BCA=\angle CAD=\alpha $$ (накрест лежащие при $$BC\parallel AD$$). Тогда $$\angle A=2\alpha =\angle D.$$ Но из $$\triangle ACD:\ \angle ADC=\frac{180{}^\circ -\alpha }{2}.$$ Тогда:

$$2\alpha =\frac{180{}^\circ -\alpha }{2}\to 4\alpha =180{}^\circ -\alpha \to \alpha =36{}^\circ \to \angle B=180-2\cdot 36=108{}^\circ $$

Аналоги к этому заданию:

Задание 7

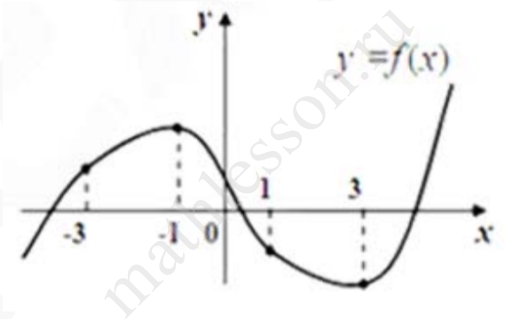
На графике функции $$у\ =\ f\ (x)$$ отмечены четыре точки с абсциссами $$-3,\ -1,\ 1,\ 3.$$ По данному графику определите, в какой из этих точек значение производной $$f'(x)$$ будет наибольшим. (В ответе укажите абсциссу этой точки).

Ответ: -3

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть $$f'\left(x\right)={\tan \alpha \ }$$, где $$\alpha$$ - угол м/у $$Ox$$ и касательной. При этом при $$\alpha \to 90{}^\circ \left(\alpha <90{}^\circ \right),\ {\tan \alpha \ }\to max\to -3$$

Аналоги к этому заданию:

Задание 8

Ребро куба $$ABCDA_1B_1C_1D_1$$ равно $$2\sqrt{5}$$. Точка $$К$$ - середина ребра $$CD$$. Найдите расстояние между прямыми $$AD$$ и $$D_1K.$$

Ответ: 2

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть Пусть DH - высота $$\triangle DD_1K.$$ Т.к. $$AD\bot \left(DCC_1\right),$$ то $$AD\bot DH\to DH$$ - общий перпендикуляр. $$DK=\frac{1}{2}DC=\sqrt{5}\to $$ из

$$\triangle DD_1K:\ D_1K=\sqrt{DD^2_1+DK^2}=5\to DH=\frac{DD_1\cdot DK}{D_1K}=2$$

Аналоги к этому заданию:

Задание 9

Найдите значение выражения $${{\log }_2 \sqrt{\sqrt{3}-1}\ }+{{\log }_4 (1+\sqrt{3})\ }$$

Ответ: 0,5

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть $${{\log }_2 \sqrt{\sqrt{3}-1}\ }+{{\log }_4 (1+\sqrt{3})\ }=$$$${{\log }_2 \sqrt{\sqrt{3}-1}\ }+\frac{1}{2}{{\log }_2 (1+\sqrt{3})\ }=$$ $$={{\log }_2 \sqrt{\sqrt{3}-1}\ }+{{\log }_2 \sqrt{\sqrt{3}-1}\ }=$$$${{\log }_2 \sqrt{3-1}\ }=0,5$$

Аналоги к этому заданию:

Задание 10

По закону Ома для полной цепи сила тока, измеряемая в амперах, равна $$I=\frac{\varepsilon }{R+r}$$, где $$\varepsilon $$ - ЭДС источника (в вольтах), $$r=2,4$$ Ом - его внутреннее сопротивление, R - сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 24\% от силы тока короткого замыкания $$I_1=\frac{\varepsilon }{r}$$? (Ответ выразите в омах).

Ответ: 7,6

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть $$\frac{\varepsilon }{R+2,4}=\frac{24}{100}\cdot \frac{\varepsilon }{2,4}\leftrightarrow$$$$ \frac{1}{R+2,4}=\frac{1}{10}\leftrightarrow R=7,6$$

Аналоги к этому заданию:

Задание 11

Первые 4 дня на строительстве объекта трудились 13 рабочих, после чего к ним присоединились еще трое, а спустя 3 дня шестеро рабочих были переведены на другой объект. За какой срок (в днях) будет построен данный объект, если шесть рабочих могут выполнить это задание за 20 дней?

Ответ: 9

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть Производительность одного рабочего $$x$$ объектов в сутки, тогда $$6x\cdot 20=1\to x=\frac{1}{120}.$$ Пусть $$y$$ дней после перевода шестерых. Тогда: $$13x\cdot 4+16x\cdot 3+10x\cdot y=1\to 100x+10xy=1\to$$$$ \frac{5}{6}+\frac{y}{12}=1\to y=2.$$ Тогда весь срок: $$4+3+2=9$$ дней.

Аналоги к этому заданию:

Задание 12

Найдите наименьшее значение функции $$f\left(x\right)=5-{{\log }_2 (31-x^2-2x)\ }$$

Ответ: 0

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Скрыть Пусть $$g\left(x\right)=31-x^2-2x\to f\left(x\right)\to min,$$ если $${{\log }_2 (31-x^2-2x)\ }\to max$$ или $$g\left(x\right)\to max.$$ Наибольшее будет в вершине параболы: $$x_0=-\frac{-2}{-2}=-1\to g\left(-1\right)=31-1+2=32\to$$$$ f\left(-1\right)=5-{{\log }_2 32\ }=0$$

Аналоги к этому заданию:

Задание 13

а) Решите уравнение $${\cos (x+\frac{\pi }{3})\ }\cdot {\cos \left(x-\frac{\pi }{3}\right)\ }=-\frac{1}{2}$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$[-\frac{\pi }{2};2\pi ]$$

Ответ: a) $$x=\pm \frac{\pi }{3}+\pi n,\ n\in Z$$; б) $$1)-\frac{\pi }{3};\ 2)\frac{5\pi }{3}; 3)\frac{\pi }{3}; 4)\frac{2\pi }{3}; 5)\frac{4\pi }{3}$$

Видео-решение Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке

а) $${\cos (x+\frac{\pi }{3})\ }\cdot {\cos \left(x-\frac{\pi }{3}\right)\ }=-\frac{1}{2}\leftrightarrow $$ $$\leftrightarrow \frac{1}{2}({\cos \left(x+\frac{\pi }{3}+x-\frac{\pi }{3}\right)\ }+{\cos \left(x+\frac{\pi }{3}-x+\frac{\pi }{3}\right)\ }=-\frac{1}{2}\leftrightarrow $$ $$\leftrightarrow {\cos 2x\ }+{\cos \frac{2\pi }{3}\ }=-1\leftrightarrow {\cos 2x\ }=-1+\frac{1}{2}=-\frac{1}{2}\leftrightarrow $$ $$\leftrightarrow 2x=\pm \frac{2\pi }{3}+2\pi n,n\in Z\leftrightarrow x=\pm \frac{\pi }{3}+\pi n,\ n\in Z.$$

б) С помощью единичной окружности отберем корни на $$\left[-\frac{\pi }{2};2\pi \right].$$ $$1)-\frac{\pi }{3};\ 2)-\frac{\pi }{3}+2\pi =\frac{5\pi }{3};3)\ 0+\frac{\pi }{3}=\frac{\pi }{3};4)\ \pi -\frac{\pi }{3}=\frac{2\pi }{3};5)\ \pi +\frac{\pi }{3}=\frac{4\pi }{3}$$

Аналоги к этому заданию:

Задание 14

Дан прямой круговой конус с вершиной М. Осевое сечение конуса - треугольник с углом $$120{}^\circ $$ при вершине М. Образующая конуса равна $$2\sqrt{3}$$. Через точку М проведено сечение конуса, перпендикулярное одной из образующих.

А) Докажите, что получившийся в сечении треугольник - тупоугольный

Б) Найдите расстояние от центра О основания конуса до плоскости сечения.

Ответ: $$\frac{\sqrt{3}}{2}$$

Решение 1 Предложить свое решение / сообщить об ошибке

Аналоги к этому заданию:

Задание 15

Решите неравенство: $${{\log }_{0,25} (1-6x)\ }\cdot {{\log }_{\left(1-x\right)} \left(\frac{1}{2}\right)\ }>1$$

Ответ: $$x\in (-4;0)\cup (0;\frac{1}{6})$$

Видео-решение Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке

$${{\log }_{0,25} (1-6x)\ }\cdot {{\log }_{\left(1-x\right)} \left(\frac{1}{2}\right)\ }>1\leftrightarrow {{\log }_{{0,5}^{-2}} \left(1-6x\right)\ }\cdot \frac{1}{{{\log }_{0,5} \left(1-x\right)\ }}>1\leftrightarrow$$ $$\leftrightarrow \frac{\frac{1}{2}{{\log }_{0,5} \left(1-6x\right)\ }}{{{\log }_{0,5} \left(1-x\right)\ }}\leftrightarrow \left\{ \begin{array}{c} {{\log }_{\left(1-x\right)} \left(1-6x\right)\ }>2 \\ 1-6x>0 \\ 1-x>0 \\ 1-x\ne 1 \end{array} \right.\leftrightarrow$$ $$\leftrightarrow \left\{ \begin{array}{c} \left(1-6x-{\left(1-x\right)}^2\right)\left(1-x-1\right)>0(1) \\ x<\frac{1}{6} \\ x<1 \\ x\ne 0 \end{array} \right.$$

$$(1): \left(1-6x-1+2x-x^2\right)\left(-x\right)>0\leftrightarrow \left(-x^2-4x\right)\left(-x\right)>0\leftrightarrow x^2\left(x+4\right)>0\leftrightarrow $$ $$\leftrightarrow x>-4.$$ Тогда: $$x\in (-4;0)\cup (0;\frac{1}{6})$$.

Аналоги к этому заданию:

Задание 16

В остроугольном треугольнике АВС провели высоты $$AH_1$$ и $$CH_2$$, затем провели луч МН, который пересекает описанную около треугольника АВС в точке К, где М - середина АС, а Н - точка пересечения высот.

А) Докажите, что $$НМ=МК$$

Б) Найдите площадь треугольника ВСК, если $$\angle ABC=60{}^\circ ;\ \angle BAC=45{}^\circ ;\ AC=1$$

Ответ: $$\frac{1}{3}$$

Решение 1 Предложить свое решение / сообщить об ошибке

Аналоги к этому заданию:

Задание 17

5-го января 2020-го года Андрей планирует положить на депозит вклад размером 3 миллиона рублей. Первые три года 2-го января банк начисляет 10% на сумму вклада, а в последующие годы банк начисляет 5% на сумму вклада.

4-го января каждого года Андрей делает дополнительный взнос на вклад так, чтобы после этого величина вклада на 5 января была больше величины вклада на 5 января прошлого года на одно и то же число. Определить общий размер начислений банка, если 3-го января 2031-го года на вкладе будет лежать 24,15 миллиона рублей.

Ответ: 7,9 млн. руб.

Видео-решение Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке

3 января 2031 года на вкладе будет сумма на 5 января 2030 года, увеличенная на 5%: $$S\cdot 1,05=24,15\to S=23$$ млн. Т.к. вклад на 5% увеличивается равномерно, то каждый год будет в сумме расти на $$\frac{23-3}{2030-2020}=2$$ млн.

2020: № года: - ; вклад 2 января: - ; добавил на вклад 4 января: - ; вклад 5-го января: 3

2021: № года: 1; вклад 2 января: $$3+0,1\cdot 3$$; добавил на вклад 4 января: $$5-3,3=1,7$$; вклад 5-го января: $$5$$

2022: № года: 2; вклад 2 января: $$5+0,1\cdot 5$$; добавил на вклад 4 января: $$7-5,5=1,5$$; вклад 5-го января: $$7$$

2023: № года: 3; вклад 2 января: $$7+0,1\cdot 7$$; добавил на вклад 4 января: $$9-7,7=1,3$$; вклад 5-го января: $$9$$

2024: № года: 4; вклад 2 января: $$9+0,05\cdot 9$$; добавил на вклад 4 января: $$1,55$$; вклад 5-го января: $$11$$

2025: № года: 5; вклад 2 января: $$11+0,05\cdot 11$$; добавил на вклад 4 января: $$1,45$$; вклад 5-го января: $$13$$

2026: № года: 6; вклад 2 января: $$13+0,05\cdot 13$$; добавил на вклад 4 января: $$1,35$$; вклад 5-го января: $$15$$

$$\dots $$

2030: № года: 10; вклад 2 января: $$21+0,05\cdot 21$$; добавил на вклад 4 января: $$0,95$$; вклад 5-го января: $$23$$

2031: № года: 11; вклад 2 января: $$23+0,05\cdot 23=24,15$$;

Начисления банка составят: $$0,1\left(3+5+7\right)+0,05(9+11+13+15+17+19+21+23)=$$ $$=0,1\cdot 15+0,05\cdot \frac{9+23}{2}\cdot 8=1,5+6,4=7,9\ $$млн. руб.

Аналоги к этому заданию:

Задание 18

Найдите все значения параметра $$a$$, при каждом из которых система уравнений $$\left\{ \begin{array}{c} 2^{2-2y^2}+{\left(\left|x\right|-2\right)}^2=8 \\ 2^{1-y^2}+x=a \end{array} \right.$$ будет иметь ровно 1 решение.

Ответ: -2;2;6

Решение 1 Решение 2 Решение 3 Предложить свое решение / сообщить об ошибке

Аналоги к этому заданию:

Задание 19

Назовем натуральное число «замечательным», если оно самое маленькое среди натуральных чисел с такой же, как у него, суммой цифр.

а) Чему равна сумма цифр две тысячи пятнадцатого замечательного числа?

б) Сколько существует двухзначных замечательных чисел?

в) Какой порядковый номер замечательного числа 5999?

г) Чему равна сумма всех четырехзначных замечательных чисел?

Ответ: а)2015 б)9 в)32 г)53991

Решение 1 Предложить свое решение / сообщить об ошибке