379 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 2
A – попадет 4 раза в мишень
B – попадет 5 раз в мишень
По формуле Бернулли:
$$P(A+B)=P(A)+P(B)=C^4_50,84\cdot0,2+0,85=0,73728$$
Задание 3
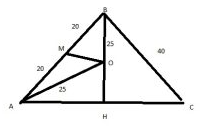
OM – высота и медиана в равнобедренном треугольнике ABO
$$\cos\angle OBA=\frac{20}{25}=0,8$$
$$\sin\angle OBA=\sqrt{1−0,8^2}=0,6$$
$$\sin\angle OBA=\frac{AH}{40}=0,6$$
$$AH=24$$
$$AC=2AH=48$$
Задание 4
$$\frac{(\lg2+2)^2}{\lg2}-\frac{(\lg2-2)^2}{\lg2}=\frac{(\lg2+2-\lg2+2)(\lg2+2+\lg2-2)}{\lg2}=8$$
Задание 5
Заметим, что середина ребер куба является центром сферы, диаметр которой равен ребру куба $$1,8=2\cdot0,9,$$ значит в кубе содержится $$\frac{1}{4}$$ сферы и, соответственно, $$\frac{1}{4}$$ ее поверхности
$$\frac{1}{4}4\pi 0,9^2=0,81\pi$$
Ответ: $$0,81$$
Задание 7
Задание 8
$$k=\frac{100−x}{100}$$ – коэффициент уменьшения веса спортсмена
$$62,5k^2=57,6$$
$$k=\frac{24}{25}$$
$$x=4\%$$
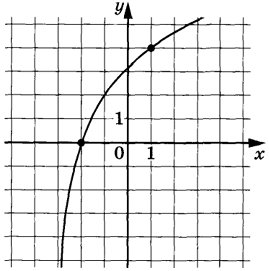
Задание 9
$$f(x)$$ проходит через $$(-2;0)$$ и $$(1;4).$$ Получим:
$$\left\{\begin{matrix} 0=\log_a(-2+b)\\ 4=\log_a(1+b) \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -2+b=1\\ 4=\log_a(1+3) \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=3\\ a^4=4 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=3\\ a=\pm\sqrt{2} \end{matrix}\right.$$
Так как $$a>0,$$ то $$a=\sqrt{2}.$$ Получим: $$f(x)=\log_{\sqrt{2}}(x+3)$$
$$f(13)=\log_{\sqrt{2}}16=8$$
Задание 10
A – 2 белых шара и 1 черный шар
B – есть черный шар (т.е. может быть 1 черный шар и 2 белых, 2 черных и 1 белый, 3 черных)
$$P(A|B)=\frac{P(AB)}{P(B)}$$
$$P(B)=P(B_1)+P(B_2)+P(B_3)$$
$$B_1$$ – 1 черный и 2 белых
$$B_2$$ – 2 черных и 1 белый
$$B_3 $$– 3 черных
$$P(B_1)=3\cdot\frac{7}{21}\cdot\frac{14}{20}\cdot\frac{13}{19}\quad$$ 3 стоит, т.к. черный шар можем взять 1-ым, 2-ым или 3-им
$$P(B_1)=3\cdot\frac{7}{21}\cdot\frac{6}{20}\cdot\frac{14}{19}$$
$$P(B_1)=\frac{7}{21}\cdot\frac{6}{20}\cdot\frac{5}{19}$$
$$P(AB)=3\cdot\frac{7}{21}\cdot\frac{14}{20}\cdot\frac{13}{19}$$
Подставляем все в формулу
Ответ: $$0,66$$
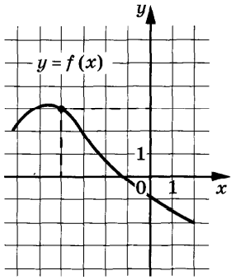
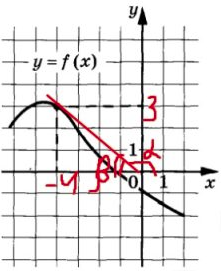
Задание 11
$$y(x)$$ будет принимать наименьшее значение, когда $$f(x)=x^5−5x^4+5x^3+37$$ будет принимать наименьшее значение
$$f'(x)=0$$
$$5x^4−20x^3+15x^2=0$$
$$x^2(5x^2−20^x+15)=0$$
$$x^2(x^2−4x+3)=0$$
$$x=0$$
$$x=3$$ – точка минимума по методу интервалов
$$x=1$$
$$y(3)=1$$