240 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 240 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №240 (alexlarin.com)
Решаем ЕГЭ 240 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №240 (alexlarin.com)
Задание 1
Таксист за месяц проехал 5500 км. Стоимость 1 л бензина 32 рубля. Средний расход бензина на 100 км составляет 9 л. Сколько рублей потратил таксист на бензин за этот месяц?
$$\frac{5500}{100}=55$$ заправок по 9 литров 55*9=495(л)-всего заправил 495*32=15840 рублей
Задание 2
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4‐го класса по математике в 2007 году по 100500 – бальной шкале. По данным диаграммы найдите число стран, в которых средний балл заключен между 495 и 515.
Австрия, Швеция и Италия
Задание 3
Площадь треугольника АВС равна 28. DE – средняя линия. Найдите площадь трапеции ABDE.
1)$$AB\left | \right |ED\Rightarrow \Delta ABC\approx \Delta CED$$ 2)$$\frac{ED}{AB}=\frac{1}{2}\Rightarrow \frac{S_{CED}}{S_{ABC}}=\frac{1}{2}^{2}\Rightarrow S_{CEP}=\frac{1}{4}*S_{ABC}=7$$ 3)$$S_{ABDE}=S_{ABC}-S_{CED}=28-7=21$$;
Задание 4
Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно и не проходя дважды по одной и той же дорожке. Схема дорожек показана на рисунке. Найти вероятность того, что Павел Иванович попадет в точку G. Результат округлите до сотых.
Путь к G: ACG или ABFCG.Вероятность выбора дорожки вычисляется ,как отношение единицы к общему количеству дорожек из точки: $$AC=\frac{1}{2}; CG=\frac{1}{3};$$ $$AB=\frac{1}{2}; BF=\frac{1}{3}; FC=1;$$ $$ACG:\frac{1}{2}*\frac{1}{3}=\frac{1}{6};$$ $$ABFCG: \frac{1}{2}*\frac{1}{3}*1*\frac{1}{3}=\frac{1}{18}$$ $$p=\frac{1}{6}+\frac{1}{18}=\frac{2}{9}\approx 0,22;$$
Задание 5
1)$$\smile AB=\angle AOB$$(свойство центрального угла)
2)$$\angle OAC=90$$(свойство касательной)$$\Rightarrow \angle AOC=90-\angle ACO=28\Rightarrow \smile AB=28$$
Задание 6
Функция $$y=f(x)$$ определена на интервале (‐5;6). На рисунке изображен график функции $$y=f(x)$$. Найдите среди точек $$x_{1}, x_{2},...,x_{7}$$ те точки, в которых производная функции $$f(x)$$ равна нулю. В ответ запишите количество найденных точек.
Дан график функции, следовательно ищем точки максимума и минимума ( в них $${f}'\left ( x \right )=0$$: $$x_{2};x_{5};x_{7}$$
Задание 7
В кубе ABCDA1B1C1D1 найдите угол между прямыми ВА1 и АС. Ответ дайте в градусах.
1)$$A_{1}B\left | \right |D_{1}C\Rightarrow$$ угол между BA_{1} и AC такой же, как между $$D_{1}C$$ и AC 2)Рассмотрим $$\Delta ADC:AD_{1}=D_{1}C=AC$$(диагонали граней куба)$$\Rightarrow$$ все углы по 90 градусов
Задание 8
Найдите значение выражения $$\frac{\sqrt{\sqrt[6]{a^{5}}}}{\sqrt[3]{\frac{1}{64}\sqrt[4]{a}}}$$, при а=216
$$\frac{\sqrt{\sqrt[6]{\alpha ^{5}}}}{\sqrt[3]{\frac{1}{64}*\sqrt[4]{\alpha }}}=$$$$\frac{((a^{5})^{\frac{1}{6}})^{\frac{1}{2}}}{(\frac{1}{64}*a^{\frac{1}{4}})^{\frac{1}{3}}}=$$$$\frac{\alpha ^{5*\frac{1}{6}*\frac{1}{2}}}{\frac{1}{4}*\alpha ^{\frac{1}{4}*\frac{1}{5}}}=$$$$\frac{4*\alpha ^{\frac{5}{12}}}{\alpha ^{\frac{1}{12}}}=$$$$4*\alpha ^{\frac{5}{12}-\frac{1}{2}}=$$$$4*\alpha ^{\frac{1}{3}}=4*\sqrt[3]{216}=4*6=24$$
Задание 9
На верфи инженеры проектируют новый аппарат для погружения на большие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выраженная в ньютонах, будет определяться по формуле $$F_{A}=\alpha \rho gr^{3}$$ , где $$\alpha =4,2$$ ‐ постоянная, r - радиус аппарата в метрах, $$\rho=1000$$ кг/м3 – плотность воды, а g ‐ ускорение свободного падения (считайте g = 10 Н/кг). Каков может быть максимальных радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 14 406 000 Н? Ответ дайте в метрах.
$$Fa=\alpha*\rho *g *r^{3}\Rightarrow r^{3}=$$$$\frac{F^{\alpha }}{\alpha *\rho *g}\Leftrightarrow $$$$r=\sqrt[3]{\frac{F_{\alpha }}{\alpha *\rho *g}}; r=\sqrt[3]{\frac{14406*10^{3}}{4,2*10^{3}*10}}=$$$$\sqrt[3]{\frac{14406}{42}}=\sqrt[3]{343}=7$$
Задание 10
За первый час автомобиль проехал 100 км, следующие два часа он ехал со скоростью 90 км/ч, затем автомобиль сломался. Через час приехал эвакуатор и за шесть часов отвез его обратно к месту оправления. Найдите среднюю скорость автомобиля за все время путешествия.
1)$$S_{1}=100$$ км; $$S_{2}=2*90=180$$ км$$\Rightarrow S_{3}=\left ( 100+180 \right )*2=560$$ км 2)$$t_{1}=1; t_{2}=2; t_{3}=6;\Rightarrow t=1+2+6=9$$ часов –время движения. Еще было ожидание 1 час, тогда общее время: t=1+9=10 часов Средняя скорость: $$v=\frac{560}{10}=56$$ км\ч
Задание 11
Найдите наименьшее значение функции $$y=4\cos x +13x +9$$ на отрезке $$[0;\frac{3\pi}{2}]$$
$$y=4*\cos x+13*x+9$$ $${y}'=-4*\sin x+13$$
Минимальное значение $$-4*\sin x$$ состовляет -4, когда $$\sin x=1 \Rightarrow {y}'_{min}=-4+13=9> 0$$
Т.е. значение производной положительно на всей $$D(f) \Rightarrow y_{min}=y(0)$$. $$y_{min}=4*\cos 0+13*0+9=4+9=13$$
Задание 12
a)$$2*\sin*\left ( x+\frac{\pi }{3} \right )-\sqrt{3}*\cos 2x=\sin x+\sqrt{3};$$
$$2*\left ( \sin x*\cos \frac{\pi }{3}+\sin\frac{\pi }{3}*\cos x \right )-\sqrt{3}*\cos 2x-\sin x-\sqrt{3}=0;$$
$$2*\sin x*\frac{1}{2}+2*\frac{\sqrt{3}}{2}*\cos x-\sqrt{3}*\cos 2x-\sin x-\sqrt{3}=0$$
$$\sqrt{3}*\cos x-\sqrt{3}* \cos 2x-\sqrt{3}=0;$$
$$\cos x- \cos 2x-1=0\Leftrightarrow$$$$\cos x-(2\cos^{2} x-1)-1=0$$
$$\cos x-2* \cos ^{2}x=0$$
$$\cos x *\left ( 1-2*\cos x \right )=0$$
$$\left [ \begin{matrix}cos x=0 & & \\1-2*\cos x=0 & &\end{matrix}\right.\Leftrightarrow \left [ \begin{matrix}x=\frac{\pi }{2}+\pi* k,k\varepsilon Z & & \\x=\pm \frac{\pi }{3}+2*\pi *n.n\varepsilon Z & &\end{matrix}\right.$$
б)Найдем частные случаи корней, принадлежащие выбранному промежутку (синим цветом):
$$-2*\pi +\frac{\pi }{3}=-\frac{5*\pi }{3}$$
$$-2*\pi+\frac{\pi}{2}=-\frac{3*\pi}{2}$$
$$-\pi+\frac{\pi}{2}=-\frac{\pi}{2}$$
Задание 13
Дана четырехугольная пирамида SABCD с вершиной S и прямоугольником ABCD в основании. Известно, что SA=SB=SC=SD=13, AD=BC=12, AB=CD=5. Из точки А на ребро SC опущен перпендикуляр АН.
а) 1) $$AC=\sqrt{AD^{2}+FC^{2}}=\sqrt{12^{2}+5^{2}}=13$$(ABCD-прямоугольник)
2) AS=SC по b условию $$\Rightarrow AS=SC=AC\Rightarrow \Delta ASC$$-равносторонний. Тогда AH-высота, медиана $$\Rightarrow SH=HS$$.
б)1)Построим $$CM\perp SB$$ и $$HK\perp SB$$; $$CH=HS$$ и $$CM\left | \right |HK$$, то $$HK=\frac{1}{2}*CM$$
2) из $$\Delta SBC$$:
$$\cos B =\frac{SB^{2}+CB^{2}-SC^{2}}{2*SB*CD}=$$$$\frac{13^{2}+12^{2}-13^{2}}{2*12*13}=\frac{6}{13}$$
$$\sin B =\sqrt{1-\cos^{2}\beta }=\frac{\sqrt{133}}{13}$$
3) из $$\Delta BMC$$:
$$MC=CB*\sin B =\frac{12*\sqrt{133}}{13}\Rightarrow$$ $$HK=\frac{6*\sqrt{133}}{13}$$
Задание 14
Решите неравенство: $$\frac{3^{2x}-54*(\frac{1}{3})^{2(x+1)}-1}{x+3}\leq 0$$
$$\frac{3^{2x}-54*\frac{1}{3}^{2*\left ( x+1 \right )}-1}{x+3}\leq 0$$
ОДЗ: $$x+3\neq 0\Leftrightarrow x\neq -3\Leftrightarrow$$$$ x\in \left ( -\infty ;-3 \right )\bigcup \left ( -3;+\infty \right )$$
$$\frac{3^{2x}-54*\frac{1}{3}^{2x+2}}{x+3}\leq 0$$
$$\frac{3^{2x}-54*\frac{1}{9}*\frac{1}{3}^{2x}-1}{x+3}\leq 0$$
Замена: $$3^{2x} =y\Rightarrow \frac{1}{3}^{2x}=\frac{1}{y}$$
$$y-\frac{6}{y}-1=\frac{y^{2}-y-6}{y}=\frac{\left ( y-3 \right )*\left ( y+2 \right )}{y}$$
Обратная замена:$$y=3^{2x}$$
$$\frac{\left ( 3^{2x}-3 \right )*\left ( 3^{2x}+2 \right )}{3^{2x*\left ( x+3 \right )}}\leq 0|*\frac{3^{2x}}{3^{2x}+2}$$
$$\frac{3^{2x}-3}{x+3}\leq 0\Leftrightarrow \frac{2x-1}{x+3}\leq 0$$
Отметим значения ,когда числитель равен и знаменатель не равен нулю. Расставим знаки значений, которые принимает выражение слева от нуля на полученных промежутках:
Нам необходимы неполжительные значения. Тогда ответом будет $$x \in (-3;0,5]$$
Задание 15
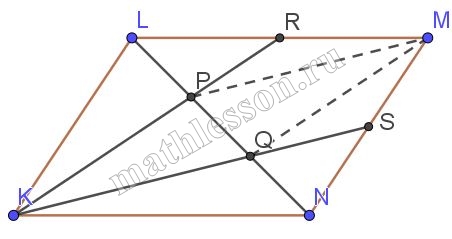
На диагонали LN параллелограмма KLMN отмены точки Р и Q, причем LP=PQ=QN
а)1) Построим MQ:NQ=PL;
$$NM=KL \angle QLM=\angle KLP\Rightarrow \Delta KLP=\Delta QMN$$ и $$MQ=KP$$
2)Аналогично, построим MP из равенства $$\Delta LMP$$ и $$\Delta KQN$$ MP=KQ;
3)из п.1 и п.2= KPMQ-паралелограмм $$\Rightarrow MP\left | \right |KQ$$,тогда по т. Фалеса т.к. PQ=QN, то MS=SN , аналогично : $$\angle P=PQ$$, тогда $$\angle R=RM$$;
б )1) Пусть $$S_{KLMN}=S$$,тогда $$S_{MLN}=\frac{1}{2}*S$$.
2) $$\frac{S_{RLP}}{S_{MLN}}=\frac{RL*LP}{ML*LN}=$$$$\frac{\frac{1}{2}*ML*\frac{1}{3}*LN}{ML*LN}=$$$$\frac{1}{6}\Rightarrow S_{RLP}=\frac{1}{6}*S_{MLN}$$.
3)Аналогично п2: $$S_{QNS}=\frac{1}{6}*S_{MNL}\Rightarrow S_{MRPQS}=S_{MLN}-2*\frac{1}{6}*S_{MNK}=$$$$\frac{2}{3}*S_{MKN}=\frac{1}{2}*\frac{2}{3}*S=\frac{1}{3}*S$$.
4)$$\frac{S_{KLMN}}{S_{MRPQS}}=\frac{1}{3}*S=\frac{3}{1}$$
Задание 16
В июле планируется взять кредит в банке в размере S тыс. рублей (S – натуральное число) сроком на 3 года. Условия возврата кредита таковы: ‐ каждый январь долг увеличивается на 22,5% по сравнению с концом предыдущего года; ‐ в июне каждого года необходимо выплатить одним платежом часть долга; ‐ в июле каждого года величина долга задается таблицей
| Год | 2018 | 2019 | 2020 | 2021 |
| Долг, тыс.руб | S | 0,7S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Каждая выплата состоит из начисленных за текущий год процентов и разницы долга между следующими и текущими: 2018: S*0,225-начисленный процент; S-0,7; S-разница долга,тогда общий платеж; $$S*0,225+0,3*S=0,525S=\frac{21}{49}*S$$ 2019: $$0,7*S*0,225+\left ( 0,7*S-0,4*S\right )=0,1575*S+0,3S=0,4575*S=\frac{183}{400}*S$$ 2020: $$0,4*S*0,225*S+\left ( 0,4*S-0\right )=0,49*S=\frac{49}{100}*S$$ Чтобы были все целые,то S должна быть кратными для 40;100 и 400$$\Rightarrow S=400$$
Задание 17
Найдите все значения параметра a, при каждом из которых уравнение $$x^{4}-2x^{3}-(2a+3)x^{2}+2ax+3a+a^{2}=0$$ имеет решения, и определите то решение, которое получается только при единственном значении параметра a .
Преобразуем данное уравнение относительно переменной а (х будет параметром): $$x^{4}-2x^{3}-(2a+3)x^{2}+2ax+3a+a^{2}=0\Leftrightarrow$$$$x^{4}-2x^{3}-2ax^{2}+3x^{2}+2ax+3a+a^{2}=0\Leftrightarrow$$$$a^{2}+a(3+2x-2x^{2})+x^{4}-2x^{3}-3x^{2}$$
Найдем корни данного уравнения:
$$D=(3+2x-2x^{2})^{2}-4(x^{4}-2x^{3}-3x^{2})=4x^{2}+12x+9=(2x+3)^{2}$$
$$a_{1}=\frac{2x^{2}-2x-3+|2x+3|}{2}$$
$$a_{2}=\frac{2x^{2}-2x-3-|2x+3|}{2}$$
Рассмотрим график функции $$a_{1}(x)$$, раскроем модуль:
$$\left\{\begin{matrix}x\geq -1,5\Rightarrow a=x^{2}\\x< -1,5\Rightarrow a=x^{2}-2x-3\end{matrix}\right.$$
Рассмотрим график функции $$a_{2}(x)$$, раскроем модуль:
$$\left\{\begin{matrix}x\geq -1,5\Rightarrow a=x^{2}-2x-3\\x< -1,5\Rightarrow a=x^{2}\end{matrix}\right.$$
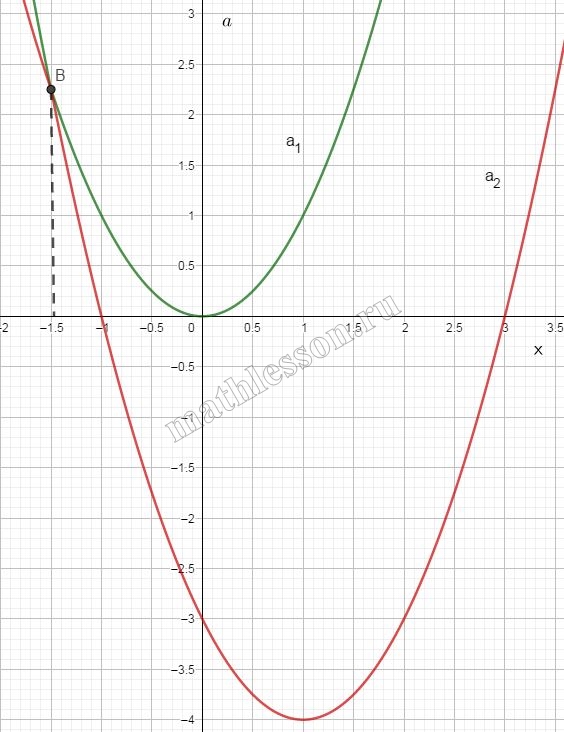
Построим графики функций $$a_{1}(x);a_{1}(x)$$:
Как видим, значения $$a$$ начинаются с -4 (вершина параболы $$a_{2}(x)$$). С учетом свойств квадратичной функции, получаем, что $$a \geq -4$$. При этом значение х, пределяемое единственным значением а равно -1,5 (абсцисса точки пересечение графиков обеих квадратичных фукнций)
Задание 18
В течение четверти учитель ставил школьникам отметки «1», «2», «3», «4» и «5». Среднее арифметическое отметок ученика оказалось равным 4,7.
а) Пусть n - число отметок, $$S_{n}$$ - сумма всех отметок. Тогда $$n, S_{n} \in N$$ и $$4,7*n=S_{n}\Leftrightarrow$$$$\frac{47}{10}*2=S_{n}$$. Так как 47 - число простое, то, чтобы выполнялось условие натуральности числа отметок и их суммы, n должно быть кратно 10. Следовательно, $$n_{min}=10$$. Пример: 7 пятерок и 3 четверки
б) Пусть n=10, тогда $$S_{n}=10*4.7-47$$. Вычтем единицу, получим $$S1_{n}=47-1=46$$, а количество оценок $$n1=10-1=9$$, но тогда среднее будет $$\frac{46}{9}=5,(1)$$, что больше 5, следовательно, невозможно. Тогда n=20
в) Уберем 3+3+5+5=16, но добавим 4+4=8 к сумме, тогда новая сумма будет на 8 меньше первоначальной. Аналогично уберем 4 числа, а добавим 2, то есть количество чисел уменьшится на 2. Тогда новое среднее: $$\frac{4,7*n-8}{n-2}$$. Найдем разность нового и старого: $$\frac{4,7*n-8}{n-2}-4,7=$$$$\frac{4,7*2-9,4+1,4}{n-2}-4,7=$$$$\frac{4,7(n-2)+1,4}{n-2}-4,7=$$$$4,7+\frac{1,4}{n-2}-4,7=\frac{1,4}{n-2}$$. Количество числе не может быть равно 10, так как если среди них две тройки, то на остальные 8 приходится $$47-2*3=41$$, тогда среднее $$\frac{41}{8}>5$$. Следовательно, n=20, тогда разница составит: $$\frac{1,4}{20-2}=\frac{7}{90}$$