383 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$4^x+6^x=2\cdot9^x$$
Разделим на $$6^x$$:
$$(\frac{2}{3})^x+1=2\cdot(\frac{3}{2})^x$$
Замена $$(\frac{2}{3})^x=t, t>0.$$ Тогда:
$$t+1=\frac{2}{t}$$
$$t^2+t-2=0$$
$$t=-2$$ - посторонний
$$t=1$$
$$(\frac{2}{3})^x=1$$
$$x=0$$
Задание 2
Всего исходов (двузначных чисел) $$99−10+1=90$$
Чисел содержащих 5: $$15,25,35,45,50,51,…59,65,…,95$$ – всего их 18
$$P(A)=\frac{18}{90}=0,2$$
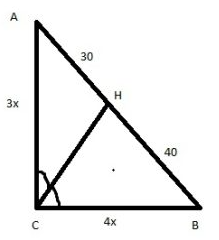
Задание 3
По св-ву биссектрисы:
$$\frac{AC}{CB}=\frac{30}{40}$$
Запишем теорему Пифагора:
$$9x^2+16x^2=70^2$$
Откуда:
$$x^2=196$$
$$S=0,5\cdot3x\cdot4x=6x^2=1176$$
Задание 4
Рассмотрим выражение
$$\tg α+\tg β=\frac{\sin α}{\cos α}+\frac{\sin β}{\cos β}=\frac{\sin α\cos β+\sin β\cos α}{\cos α\cos β}=\frac{\sin(α+β}{\cos α\cos β}$$
Итоговая формула
$$\tg α±\tg β=\frac{\sin(α±β)}{\cos α\cos β}$$
Используя ее можно преобразовать наше выражение
$$\frac{\sin90}{\cos9\cos81}-\frac{\sin90}{\cos63\cos27}=\frac{1}{\cos9\cos(90-9)}-\frac{1}{\cos(90-27)\cos27}=$$
$$=\frac{1}{\sin9\cos9}-\frac{1}{\sin27\cos27}=\frac{2}{\sin18}-\frac{1}{\sin54}=$$
$$=2\frac{\sin54-\sin18}{\sin54\sin18}=2\frac{2\sin18\cos36}{\sin54\sin18}=$$
$$=4\frac{\cos(90-54)}{\sin54}=4$$
Задание 5
$$V=\frac{1}{3}S_{осн}SO$$
$$S_{осн}=14\cdot14\sin60$$
$$SO=OM,$$ т.к треугольник SOM – прямоугольный и равнобедренный
$$SO=OM=\frac{S}{p}=\frac{14\cdot14\cdot\frac{\sqrt{3}}{2}}{0,5\cdot4\cdot14}=\frac{7\sqrt{3}}{2},$$ где p – полупериметр
Подставляя, получаем ответ 343
Задание 6
$$v(t)=x′(t)=2t−13$$
Проекция скорости будет уменьшаться (увеличиваться), когда она будет меньше (больше) нуля, то направление движения поменяется, найдем этот момент
$$v(t)=0$$
$$t=\frac{13}{2}=6,5$$
Задание 7
$$\frac{4\cdot3900\cdot10}{\pi D^2}\leq\frac{624000}{\pi}$$
$$D^2\geq\frac{1}{4}$$
Диаметр не может быть отрицательным, значит
$$\geq\frac{1}{2}$$
Задание 8
Обозначим производительность трех бригад как $$x,y,z$$ соответственно
Тогда составим уравнения из условия. Возьмем всю работу $$A=1$$ для удобства
$$4(x+y+z)=1$$
$$6(x+z)=1$$
$$8(x+y)=1$$
Решая систему
$$\frac{z}{y}=1,5$$
Задание 10
По формуле Бернулли
$$P(ν=k)=C^k_np^k\cdot q^{n−k}, ν$$ – число успехов в n независимых испытаниях
$$p=q=0,5$$ – по условию
Нам нужно найти
$$P(ν>3)=P(ν=4)+..+P(ν=10)$$
Но как известно
$$P(ν>3)=1−P(ν\leq3)$$
$$P(ν\leq3)=P(ν=0)+P(ν=1)+P(ν=2)+P(ν=3)$$
$$P(ν=0)=C^0_{10}(\frac{1}{2})^{10}$$
$$P(ν=1)=C^1_{10}\cdot\frac{1}{2}\cdot(\frac{1}{2})^9$$
Далее по аналогии
Задание 11
$$y′=\frac{−x^2+10x+144}{(x^2+144)^2}=0$$
$$x=18$$ – т. максимума
$$x=−8$$ – т. минимума
Задание 13
Задание 15
| Срок вклада | 1-2 месяца | 3-4 месяца | 5-6 месяцев |
|---|---|---|---|
| Ставка в % годовых | 6% | 18% | 12% |