401 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
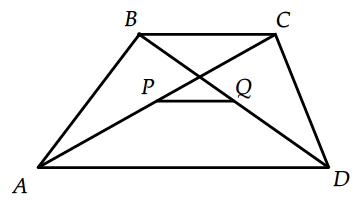
Задание 1
Отрезок, соединяющий середины диагоналей трапеции равен полуразности большего и меньшего оснований. Поэтому он равен
$$\frac{14-7}{2}=3,5$$
Задание 2
Рассчитаем скольким условным единицам будет равняться третье измерение (обозначив его за $$c$$) заданной фигуры, если нам известно, согласно условиям этого задания, что первые два измерения равняются 4 и 10, в то время как площадь поверхности составляет 304:
$$2(4\cdot c + 4\cdot10 + 10\cdot c) = 304$$
$$80+28c=304$$
$$28c=224$$
$$c=8$$
Рассчитаем скольким кубическим условным единицам будет равняться объем заданного параллелепипеда:
$$4\cdot10\cdot8 = 320$$
Задание 3
После того как выловили и пометили 5 щук в пруде оказалось 5 помеченных щук и 35 без метки.
Количество исходов при выборе 2 щук из 5 помеченных: $$C^2_5 = \frac{5!}{2!\cdot(5-2)!} = 10$$
Количество исходов при вылове 7 щук из 35 без метки: $$C^{7}_{35}=\frac{35!}{7!\cdot(35-7)!)}=29\cdot30\cdot...\cdot\frac{35}{1\cdot2\cdot...\cdot7)} = 6724520$$
Общее количество исходов при вылове 9 щук из 40: $$C^9_{40}=\frac{40!}{9!\cdot(40 - 9)!}=32\cdot33\cdot...\cdot\frac{40}{1\cdot2\cdot...\cdot9} = 273438880$$
Вероятность выловить 2 помеченные щуки: $$P(2) = C^2_5\cdot\frac{C_{35}^7}{C_{40}^9} = 10\cdot\frac{6724520}{273438880} = 0,246.$$
Задание 4
$$p=p_1\cdot p_2\cdot q_3+p_1\cdot q_2\cdot p_3+q_1\cdot p_2\cdot p_3+p_1\cdot p_2\cdot p_3=$$
$$=0,4\cdot0,5\cdot0,4+0,4\cdot0,5\cdot0,6+0,6\cdot0,5\cdot0,6+0,4\cdot0,5\cdot0,6=$$
$$=0,08+0,12+0,18+0,12=0,5$$
Задание 5
ОДЗ:
$$1,6-6x>0$$
$$-6x>-1,6$$
$$x<\frac{-1,6}{-6}$$
$$x<\frac{4}{15}$$
$$16x-0,6>0$$
$$16>0,6$$
$$x>\frac{3}{80}$$
$$x\in(\frac{3}{80};\frac{4}{15})$$
Решение:
$$\log_4(1,6-6x)=\log_4(16x-0,6)-1$$
$$\log_4(1,6-6x)=\log_4(16x-0,6)-\log_4 4$$
$$\log_4(1,6-6x)=\log_4((16x-0,6):4)$$
$$\log_4(1,6-6x)=\log_4(4x-0,15)$$
$$1,6-6x=4x-0,15$$
$$-4x-6x=-1,6-0,15$$
$$-10x=-1,75$$
$$x=0,175$$
$$\frac{3}{80}<0,175<\frac{4}{15}$$
Задание 6
$$\log_{0,8}\log_{144}288\sqrt{3}=\log_{0,8}\log_{12^2}144\cdot2\sqrt{3}=\log_{0,8}\log_{12^2}12^2\cdot(4\cdot3)^{\frac{1}{2}}=$$
$$=\log_{0,8}\log_{12^2}12^2\cdot12^{\frac{1}{2}}=\log_{0,8}\log_{12^2}12^{2,5}=\log_{0,8}\frac{2,5}{2}=\log_{\frac{4}{5}}\frac{5}{4}=-1$$
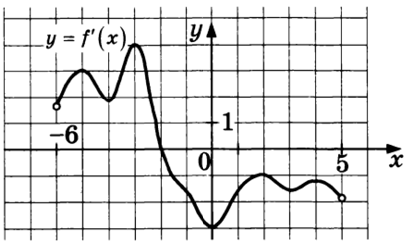
Задание 7
Точка экстремума на графике производной – точка пересечения с осью Ox: -2.
Задание 8
Согласно понятиям термодинамики, в каждом состоянии газ характеризуется определенными параметрами – давлением, объемом, температурой.
По условию задачи, газ переходит из одного состояния в другое так, что $$pV^a=const$$
Это значит, что
$$p_1V_1^a=p_2V_2^a$$
$$\frac{p_1}{p_2}=(\frac{V_2}{V_1})^2$$
Давление уменьшилось не менее чем в 32 раза, то есть
$$\frac{p_1}{p_2}\geq32$$
Значит,
$$(\frac{V_2}{V_1})^2\geq32$$
$$16^a\geq32,$$ отсюда $$а\geq1,25$$
Наименьшее значение для а записываем в ответ.
Задание 9
Пусть производительность труб $$а,в,с,х$$ литров в час соответственно. Примем объем всего бассейна за 1.
Тогда $$в+с+х=1$$
$$(а+с+х)\cdot\frac{1}{4} = 1$$
$$(а+в)\cdot\frac{2}{3} = 1$$
Получили систему:
$$в+с+х=1$$
$$а+с+х= \frac{4}{5}$$
$$а+в=\frac{3}{5}$$
Сложим все уравнения:
$$2(а+в+с+х)= 1+\frac{3}{5}+\frac{4}{5}$$
$$2(а+в+с+х) = \frac{12}{5}$$
$$а+в+с+х = \frac{6}{5}$$ литров в час - совместная производительность
$$1:\frac{6}{5}=\frac{5}{6} ч=\frac{5}{6}\cdot60=50$$ минут
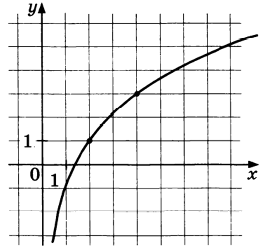
Задание 10
График проходит через $$(2;1)$$ и $$(4;3).$$ Тогда:
$$\left\{\begin{matrix} 1=b+\log_a 2\\ 3=b+\log_a 4 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1=b+\log_a 2\\ 2=\log_a 4-\log_a 2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1=b+2\\ \log_a 2=2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b=-1\\ a=\sqrt{2} \end{matrix}\right.$$
Получим:
$$f(x)=-1+\log_{\sqrt{2}} x\Rightarrow f(0,5)=-1+\log_{\sqrt{2}}\frac{1}{2}=-1-2=-3$$
Задание 11
$$(x^3-\frac{48}{x^2})' = \frac{3(x^5+32)}{x^3}$$
Точки экстремума:
$$\frac{3(x^5+32)}{x^3} = 0$$
$$x^5+32 = 0$$
$$x^5= -32$$
$$x= - 2$$ входит в отрезок $$[-3;2]$$
Значение функции в точке экстремума $$y(-2)=(-2)^3-\frac{48}{(-2)^2} = -20$$
Значение функции на концах отрезка $$[-3;2]:$$
$$y(-3)=(-2)^3-\frac{48}{(-2)^2} = -\frac{97}{3} =-32\frac{1}{3}$$
$$y(2)=2^3-\frac{48}{2^2}= -4$$
Наибольшее значение функции в точке $$x=2 ; y= -4$$