245 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 245 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №245 (alexlarin.com)
Решаем ЕГЭ 245 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №245 (alexlarin.com)
Задание 1
В школе уроки начинаются в 8:30, каждый урок длится 45 минут, все перемены кроме одной, длятся 10 минут, а перемена между вторым и третьим уроком – 20 минут. Сейчас на часах 13:00. Через сколько минут прозвенит ближайший звонок с урока?
Составим таблицу начала и конца уроков:
| Номер урока | Время начала | Время конца |
| 1 | 8:30 | 9:15 |
| 2 | 9:25 | 10:10 |
| 3 | 10:30 | 11:15 |
| 4 | 11:25 | 12:10 |
| 5 | 12:20 | 13:05 |
Как видим, до конца урока (звонка) осталось 5 минут
Задание 2
На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций газодобывающей компании в первые две недели ноября. 2 ноября бизнесмен приобрел 10 акций этой компании. Шесть из них он продал 6 ноября, а 13 ноября – остальные 4. Сколько рублей потерял бизнесмен в результате этих операций?
Приобрел за 2100, потратил 2100*10=21000 Продал 6 ноября за 1950, в 13 ноября за 1200 В итоге убыток составил: 21000-6*1950-4*1200=4500
Задание 3
Две противоположные стороны параллелограмма разделены на три равные части. Площадь заштрихованной части равна 7 см2. Найдите площадь параллелограмма. Ответ дайте в см2.
$$S_{ABC}=\frac{1}{2}*AB*CH=$$$$\frac{1}{2}*\frac{1}{3}*A_{1}B_{1}*HH_{1}=$$$$\frac{1}{12}S\Rightarrow$$ $$S_{2\Delta }=\frac{1}{12}*2S=\frac{1}{6}S\Rightarrow$$ $$S=6*7=42$$
Задание 4
Найдите вероятность того, что произведение трех последних цифр случайно выбранного телефонного номера четно.
Нечетное в произведении даёт только нечетное . Вероятность ,что 1 число будет нечетным $$\frac{5}{10}=\frac{1}{2}$$. Что 3 числа одновременно будут нечетным $$(\frac{1}{2})^{3}=\frac{1}{8}=0,125$$, тогда то, что четное: $$1-0,125=0,875.$$
Задание 5
Решите уравнение $$\sqrt{-2x}*\sqrt{-2x+15}=4$$ . Если уравнение имеет больше одного корня, то в ответе запишите произведение корней.
Область определения: D(f) $$\left\{\begin{matrix}-2x\geq 0\\-2x+15\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\leq 0\\x\leq 7,5\end{matrix}\right.\Leftrightarrow$$ $$x\leq 0$$ $$\sqrt{4x^{2}-30}=4\Leftrightarrow$$ $$4x^{2}-30x=16\Leftrightarrow$$ $$2x^{2}-15x-8=0$$ $$D=225+64=289=17^{2}$$ $$x_{1}=\frac{25-17}{4}=-0,5$$ $$x_{2}=\frac{15+17}{4}=8\notin D(f)$$
Задание 6
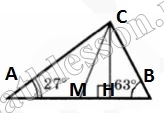
Два угла треугольника равны 63 и 27. Найдите угол между высотой и медианой, проведенными из вершины третьего угла. Ответ дайте в градусах.
Задание 7
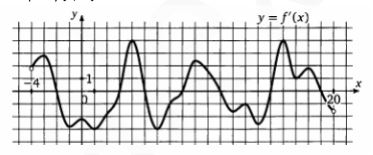
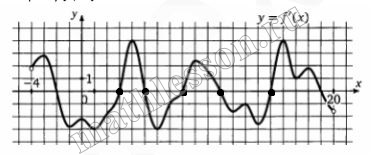
На рисунке изображен график производной функции f(x), определенной на интервале (‐4;20). Найдите количество точек экстремума функции f(x) , принадлежащих отрезку [0;18]
Точки экстремума –точки максимума и минимума, то есть когда производная равна 0 (на рисунке отмечены черными точками ). Их на данном промежутке 5.
Задание 8
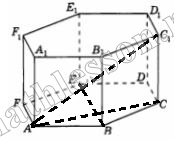
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите угол между прямыми АС1 и ВЕ.
AC- проекция ,$$AC_{1}$$ на (ABC)
$$AC\perp BE\Rightarrow AC_{1}\perp BE$$ (по тереме о трех перпендикулярах)
Задание 9
Найдите значение выражения $$\frac{2 \cos^{2}\frac{1 \pi}{10}}{ctg \frac{11\pi}{10}\sin \frac{\pi}{5}}$$
$$\frac{1 \cos ^{2}\frac{2 \pi}{10}}{ctg \frac{11\pi}{10}\sin \frac{\pi}{5}}=$$$$\frac{2 \cos ^{2}\frac{\pi}{10}}{ctg (\pi+\frac{\pi}{10})\sin \frac{2\pi}{5}}=$$$$\frac{2 \cos^{2}\frac{\pi}{10}}{ctg \frac{\pi}{10}*2 \sin \frac{\pi}{10}\cos \frac{\pi}{10}}=$$$$\frac{\cos^{2} \frac{\pi}{10}}{\cos^{2} \frac{\pi}{10}}=1$$$$
Задание 10
Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой $$h(t)=-5t^{2}+18t$$ , где h ‐ высота в метрах, t ‐ время в секундах, прошедшее с момента броска. Сколько секунд камень находится на высоте не менее 9 метров?
$$-5t^{2}+18t\geq 9$$ $$-5t^{2}+18-9\geq 0$$ $$5t^{2}-18t+9\leq 0$$ $$D=324-180=144=12^{2}$$ $$t_{1}=\frac{18+12}{10}=3$$ $$t_{2}=\frac{18-12}{10}=0,6$$ $$t=t_{1}-t_{2}=3-0,6=2,4$$
Задание 11
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 12 рабочих, а во второй – 21 рабочий. Через 10 дней после начала работы в первую бригаду перешли 12 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Пусть x-производительность одного рабочего, 1-объем работы, y- количество дней работы после перехода: $$\left\{\begin{matrix}21x*10+9x*y=1|*8 & & \\12x*10+24xy=1 |*3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}1680x+72xy=8\\360x+72xy=3\end{matrix}\right.$$ Вычтем из первого уравнения второе $$1320x=5$$ $$x=\frac{5}{1320}=\frac{1}{164}$$ $$120*\frac{1}{264}+\frac{24}{264}y=1$$ $$\frac{y}{11}=\frac{144}{264}=\frac{6}{11}$$ $$y=6$$ Общее количество дней 10+6=16
Задание 12
$${y}'=\frac{1}{2\sqrt{2\lg x-1}}*\frac{2}{x\ln 10}-\frac{1}{x\ln10}=0$$
$$\frac{1}{x\ln 10}(\frac{1}{2\sqrt{2\lg x-1}})=0$$
$$\left\{\begin{matrix}x\neq 0 \\\sqrt{2\lg x-1}=1(1)\end{matrix}\right.$$
$$(1): \sqrt{2\lg x-1}=1\Leftrightarrow$$ $$2\lg x-1\leq 1\Leftrightarrow$$ $$2\lg x=2\Leftrightarrow$$ $$\lg x=1\Leftrightarrow x=10$$
$$y(10)=y=\sqrt{2\lg 10-1}-\lg 10=1-1=0$$
Задание 13
A) Найдем область определения D(f):
$$\left\{\begin{matrix}4+3 \cos x-\cos 2x\geq 0(1) & & \\\sin x\geq 0(2) & &\end{matrix}\right.$$
Рассмотрим первое неравенство системы $$(1): 2 \cos ^{2}x-1-3 \cos x-4\leq 0$$
$$2 \cos ^{2}x-3 \cos x-5\leq 0$$
$$D=9+40=49$$
$$\cos x=\frac{3+7}{4}=2,5$$
$$\cos x=\frac{3-7}{4}=-1$$
$$\left\{\begin{matrix}\cos x\geq -1\\\cos x\leq 2,5 \end{matrix}\right.\Leftrightarrow$$ $$x \in R$$
Рассмотрим второе неравенство системы $$(2): \sin x\geq 0 \Leftrightarrow x\in [2\pi n, \pi+2\pi n], n \in Z$$
Решим данное уравнение:
$$5+3 \cos x-2 \cos^{2}x=6\sin ^{2}x=6-6 \cos ^{2}$$
$$4 \cos ^{2}+3 \cos x-1=0$$
$$D=9+16=25$$
$$\left[\begin{matrix}\cos x=\frac{-3+5}{8}=\frac{1}{4}\\\cos x=\frac{-3-5}{8}=-1\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=arccos \frac{1}{4}+2\pi n\\x=-arccos\frac{1}{4}+2 \pi n \notin D(f)\\x=-\pi+2 \pi k, k\in Z\end{matrix}\right.$$
Б) Найдем корни на заданном промежутке
Как видим корень (1) не попадает в заданный промежуток а корень (3) попадает. Найдем его: $$-\frac{7\pi}{2}+\frac{\pi}{2}=-3\pi.$$
Задание 14
Сторона основания ABCD правильной пирамиды SABCD равна 2, угол между боковым ребром и основанием равен $$arccos \frac{1}{\sqrt{5}}$$ . На ребрах Sa и SD расположены точки Е и F так, что АЕ=2ES, DF=8SF. Через точки Е и F проведена плоскость $$\alpha$$ , параллельная АВ.
A) 1) $$\Delta DCA: CA=\sqrt{2^{2}+2^{2}}=2\sqrt{2}\Rightarrow$$ (теорема Пифагора). Тогда $$OA =\frac{CA}{2}=\sqrt{2}$$
2) $$\Delta SOA: \cos SAO=\frac{1}{\sqrt{5}}\Rightarrow$$. Тогда по основному тригонометрическому тождеству $$\sin SAO =\sqrt{1-\frac{1}{5}}=\frac{2}{\sqrt{5}}\Rightarrow$$ $$tg SAO=\frac{2}{\sqrt{5}}:\frac{1}{\sqrt{5}}=2$$. $$\frac{SO}{OA}=tg SAO\Rightarrow SO=OA*tg SAO=2\sqrt{2}$$
3) $$\Delta SON: SN=\sqrt{SO^{2}+ON^{2}}=\sqrt{1+8}=3$$ (по теореме Пифаогора). По условию: $$SH=\frac{1}{3}SN=1$$; $$SL=\frac{1}{9}SN=\frac{1}{3}$$. Из подобия треугольников: $$HH_{1}=\frac{1}{3}AD=\frac{2}{3}$$, $$H_{1}L=1-\frac{1}{3}=\frac{2}{3}$$
4) $$\Delta SNN_{1}: \cos S=\frac{1^{2}+1^{2}-(\frac{2}{3})^{2}}{2*1*1}=$$$$\frac{2-\frac{4}{9}}{2}=\frac{14}{2*9}=\frac{7}{9}$$ (из теоремы косинусов). $$LN=\sqrt{\frac{1}{3}^{2}+1^{2}-2*\frac{1}{3}*1*\frac{7}{9}}=$$$$\sqrt{\frac{10}{9}-\frac{14}{27}}=\sqrt{\frac{16}{27}}=\frac{4}{3\sqrt{3}}$$ (из теоремы косинусов). $$\cos LHH_{1}=\frac{\frac{16}{27}+(\frac{2}{3})^{2}-(\frac{2}{3})^{2}}{2*\frac{2}{3}*\frac{4}{3\sqrt{3}}}=$$$$\frac{16}{27}:\frac{16}{9\sqrt{3}}=\frac{9\sqrt{3}}{27}=\frac{\sqrt{3}}{3}\Rightarrow$$ $$LHH_{1}=\frac{\sqrt{6}}{3}$$ (из теоремы косинусов)
Б) 1)$$ZH=\frac{1}{3}ON=\frac{1}{3}$$. Из $$\Delta RZH: RZ=ZH *tg LHH_{1}=$$$$\frac{1}{3}\sqrt{2}=\frac{\sqrt{2}}{3}$$. $$ZO =\frac{2}{3}SO=\frac{2*2\sqrt{3}}{3}=\frac{4\sqrt{2}}{3}$$. $$RO=ZO+RZ=\frac{5\sqrt{2}}{3}$$
2) Из $$\Delta ROW: OW =\frac{RO}{tg LHH_{1}}=$$$$\frac{\frac{5 \sqrt{2}}{3}}{\sqrt{2}}=\frac{5}{3}$$
3) $$NW=OW-ON=\frac{5}{3}-1=\frac{2}{3}$$
4) $$NO=NW*\sin LHH_{1}=$$$$\frac{2}{3}*\frac{\sqrt{6}}{3}=\frac{2\sqrt{6}}{9}$$
Задание 15
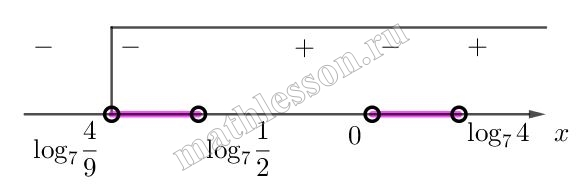
Решите неравенство $$\frac{1}{x}\log _{7}(\frac{9}{2}-2*7^{-x})>1$$
Ограничения для логарифмируемой функции:
$$\frac{9}{2}-27^{-x}>0\Leftrightarrow 2*7^{-x}<\frac{9}{2}\Leftrightarrow$$ $$7^{-x}<\frac{9}{4}\Leftrightarrow$$ $$7^{-x}<7^{\log_{7}\frac{9}{4}}\Leftrightarrow$$ $$x>-\log_{7}\frac{9}{4}=\log _{7}\frac{4}{9}$$
Решим неравенство:
$$\frac{\log_{7}(\frac{9}{2}-2*7^{-x})-x}{x}>0\Leftrightarrow \frac{\log _{7}(\frac{9}{2}-2*7^{-x})*7^{-x}}{x}>0$$$$\Leftrightarrow \frac{\frac{9}{2}*7^{-x}-1}{x}>0$$
Рассмотрим числитель : пусть $$7^{-x}=y>0$$
$$\frac{9}{2}y-2y^{2}-1=0\Leftrightarrow$$$$4y^{2}-9y+2=0\Leftrightarrow$$$$D=81-32=49$$
$$y_{1}=\frac{9+7}{8}=2$$ и $$y_{2}=\frac{9-7}{8}=\frac{1}{4}$$
В соответствии с полученными корнями разложим числитель на множители, используя формулу $$ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$$, а так же умножим на минус один обе части:
$$\frac{(7^{-x}-2)(7^{-x}-\frac{1}{4})}{x}<0\Leftrightarrow$$$$\frac{(7^{-x}-7^{\log _{7} 2)})(7^{-x}-7^{\log_{7}\frac{1}{4}})}{x}<0\Leftrightarrow$$ $$\frac{(-x-\log _{7}2)(-x-\log_{7}\frac{1}{4})}{x}<0\Leftrightarrow$$$$\frac{(x+log _{7}2)(x+log_{7}\frac{1}{4})}{x}<0$$
Учтем, что $$-\log _{7}2=\log_{7}\frac{1}{2}$$ и $$-\log_{7}\frac{1}{4}=\log_{7}4$$, а так же $$D(f)$$
$$x \in (\log_{7}\frac{4}{9}; \log _{7}\frac{1}{2})\cup (0; \log_{7}4)$$
Задание 16
Биссектриса AD и высота ВЕ остроугольного треугольника АВС пересекаются в точке О. Окружность радиуса R с центром в точке О проходит через вершину А, середину стороны АС и пересекает сторону АВ в точке К такой, что АК:КВ=1:3.
A) 1) $$\angle AKL=90=\angle AGL$$(опираются на диаметр)
2)$$\Delta AKL=\Delta AGL$$(по острому углу и гипотенузе )$$\Rightarrow AK=AC_{1}=x$$, тогда $$KB=3x\Rightarrow AB=4x, C_{1}C=x$$$$\Rightarrow AC=2x$$
3) По свойству биссектрис: $$\frac{AB}{AC}=\frac{BC}{DC}=\frac{4x}{2x}=\frac{2}{1}$$. По свойству площадей: $$\frac{S_{ABD}}{S_{ADC}}=\frac{BD}{DC}=\frac{2}{1}$$
Б) 1) $$\angle BAD=\alpha =\angle DAC\Rightarrow \angle A=2\alpha$$. Из $$\Delta ABE :\cos 2\alpha =\frac{AE}{AB}=$$$$\frac{0,5x}{4x}=\frac{1}{8}\Leftrightarrow$$$$2 \cos^{2}\alpha -1=\frac{1}{8}\Leftrightarrow$$ $$\cos ^{2}\alpha =\frac{9}{16}\Rightarrow$$ $$\cos \alpha =\frac{3}{4}$$
2) $$AL=2R=2\sqrt{2}$$. Из $$\Delta ALC_{1} :\frac{AC_{1}}{AL}=\cos \alpha \Rightarrow$$ $$AC_{1}=\frac{2\sqrt{2}*3}{4}=\frac{3\sqrt{2}}{2}\Rightarrow$$ $$AC=3\sqrt{2} AB=6\sqrt{2}$$
3) из $$\Delta ABC:$$ $$BC=\sqrt{(6\sqrt{2})^{2}+(3\sqrt{2})^{2}-2*6\sqrt{2}*3\sqrt{2}*\cos 2\alpha }=$$$$\sqrt{72+18-\frac{3*2*2*6*3}{8}}=\sqrt{90-9}=9$$
Задание 17
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» ‐ 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать на своем отеле предприниматель?
Пусть x - количество стандартных, y - количество люкс. Тогда общая площадь: $$27x+45y\leq 981\Leftrightarrow 3x+5y\leq 109(1)$$
Общая стоимость: $$2000x+4000y=max$$
Рассмотрим площадь и цену стандартного через люкс. Один стандарт занимает место $$\frac{27}{45}=\frac{3}{5}$$ люкса , то есть 6 люксовых по площади равны 10 стандартам.
При этом стоимость 6 люксов выйдет как 12 стандартов . Очевидно , что по отношению цены за единицу площади люксовый лучше, потому их и максимизируем: с учетом неравенства (1): $$5y\leq 109-3x\Leftrightarrow$$ $$y\leq \frac{109-3x}{5}\Leftrightarrow$$ $$y\leq \frac{109}{5}\Rightarrow$$ $$y=21$$. Остаётся $$4\Rightarrow 3x\leq 4\Rightarrow x=1$$
То есть 21 люкс и 1 стандарт. Тогда доход с них составит $$21*4000+1*2000=86000$$
Задание 18
При каких значениях параметра a уравнение $$\log_{5} x +4(1-a^{2})\log_{25x} 5 -2=0$$ имеет два корня, расстояние между которыми больше 24/5?
$$D(f):\left\{\begin{matrix} x>0 \\ 25x\neq 1 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix} x>0 \\ x\neq \frac{1}{25} \end{matrix}\right.$$
1) Пусть $$a=\pm 1$$,тогда $$\log_{5}x=2\Leftrightarrow x=25$$ - один корень, что не устраивает условие задания
2) Пусть $$a\neq \pm 1$$, тогда: $$\log_{5}x+\frac{4(1-a^{2})}{\log_{5}25x}-2=0\Leftrightarrow$$$$\log_{5}x+\frac{4(1-a^{2})}{\log_{5}x+2}-2=0\Leftrightarrow$$$$\log_{5}^{2}x+2\log_{5}x-2\log_{5}x-4+4-4a^{2}=0\Leftrightarrow$$$$\log_{5}^{2}x=4a^{2}\Leftrightarrow$$$$\left\{\begin{matrix} \log_{5}x=2a\\ \log_{5}x=-2a\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix} x_{1}=5^{2a}\\ x_{2}=5^{-2a}\end{matrix}\right.$$
Так как по условию задания $$\left | x_{1}-x_{2} \right |>\frac{24}{5}$$ тогда: $$\left | 5^{2a}-5^{-2a} \right |\Leftrightarrow$$. Пусть $$5^{2a}=y>0$$, тогда:
$$\left | y-\frac{1}{y} \right |>\frac{24}{5}\Leftrightarrow$$ $$\left[\begin{matrix} y-\frac{1}{y}>\frac{24}{5}\\ y-\frac{1}{y}<\frac{-24}{5}\end{matrix}\right.$$$$\Leftrightarrow \left[\begin{matrix} \frac{5y^{2}-24y-5}{y}>0 \\ \frac{5y^{2}+24y-5}{y}<0 \end{matrix}\right.$$
т.к. y>0, то $$\left[\begin{matrix} 5y^{2}-24y-5>0 \\ 5y^{2}+24y-5<0 \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} (y-5)(y+\frac{1}{5})>0 \\ (y+5)(y-\frac{1}{5})<0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} y-5>0 \\ y-\frac{1}{5}<0 \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} y>5 \\ y<\frac{1}{5} \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} 5^{2a}>5 \\ 5^{2a}<\frac{1}{5} \end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix} a>\frac{1}{2} \\ a<-\frac{1}{2} \end{matrix}\right.$$
С учётом , что $$a\neq \pm 1$$, получаем: $$a\in (-\infty ;-1)\cup (-1; -\frac{1}{2})\cup (\frac{1}{2}; 1)\cup (1 ;+\infty )$$
Задание 19
На доске написано 19 натуральных чисел (необязательно различных), каждое из которых не превосходит 11. Среднее арифметическое написанных на доске чисел равно 10. С этими числами произвели следующие действия: четные числа разделили на 2, а нечетные – умножили на 2. Пусть А – среднее арифметическое полученных чисел.
Пусть даны числа: $$a_{1}...a_{19}\in N \leq 11$$. Т.к. среднее арифметическое равно 10 , то $$\frac{a_{1}+...+a_{19}}{19}=10\Leftrightarrow \sum_{i=1}^{19}a_{i}=190$$. Пусть x-сумма четных; y-нечетных;
A) $$\left\{\begin{matrix}x+y=190\\\frac{x}{2}+2y=17*19=323\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=190-y\\x+4y=646\end{matrix}\right.$$. Тогда: $$190-y+4y=646\Leftrightarrow$$ $$3y=456\Leftrightarrow$$ $$y=152$$. Значит может.
Б) $$\left\{\begin{matrix}x+y=190\\\frac{x}{2}+2y=7*19=133\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=190-y\\x+4y=226\end{matrix}\right.$$. Тогда: $$190-y+4y=226\Leftrightarrow$$ $$3y=76\Leftrightarrow$$ $$y=\frac{76}{3}\notin N$$. Значит, не может
B) $$\left\{\begin{matrix}x+y=190\\\frac{x}{2}+4y\rightarrow max\end{matrix}\right.$$. Получаем : $$190+3y\rightarrow max$$. Чем больше y, тем больше 190+3y. Так как чисел 19, если они все нечетные , то сумма 190( четные ) не получается (сумма нечетного количества нечетных чисел - число нечетное) , следовательно, возможно, что 18 нечетных и 1четное . Так как, при увеличении y ,x уменьшается и одно число четное, то надо взять наименьшее четное - 2 и наибольшее нечетное 11 . 11*18=198, а должно быть 188. Тогда 17 чисел по 11, 1 число равно 1 и 1 число 2. Тогда: $$A=\frac{\frac{2}{2}+17*11*2+1*1*2}{19}=\frac{377}{19}$$