406 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
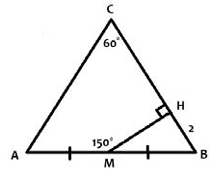
Задание 1
$$\angle HMB=180^{\circ}-150^{\circ}=30^{\circ}\Rightarrow \angle MBH=90^{\circ}-30^{\circ}=60^{\circ}\Rightarrow \Delta ABC$$ - равносторонний.
Из $$\Delta HMB: MB=\frac{HB}{\sin\angle HMB}=\frac{2}{\sin30^{\circ}}=4\Rightarrow AB=8\Rightarrow AC=8$$
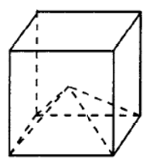
Задание 2
$$V_{куба}=72$$
$$V_{пирамиды}=\frac{1}{3}\cdot S_{ocн}\cdot h$$
$$V_{пирамиды}=\frac{1}{6}\cdot S_{куба}=\frac{1}{6}\cdot72=12$$
Задание 3
Имеем два варианта расклада с разным промежуточным состоянием 4-го мая:
а) 3-го мая солнечно, 4-го мая солнечно, 5-го мая дождливо:
$$0,7\cdot0,3=0,21,$$
б) 3-го мая солнечно, 4-го мая дождливо, 5-го мая дождливо:
$$0,3\cdot0,7=0,21$$
$$0,21+0,21=0,42$$
Задание 4
Ане нужны 4 принцессы из 10, то есть вероятность обнаружить одну из нужных принцесс при покупке равна $$0,4.$$
Вероятность того, что в очередной покупке не будет нужной принцессы равна
$$1-0,4 = 0,6.$$
Тогда вероятность того, что нужной принцессы не будет в первой покупке, но она будет в следующей равна $$0,6\cdot0,4 = 0,24.$$
Таким образом, искомая вероятность получения нужной принцессы после одной или двух покупок:
$$0,4+0,24 = 0,64.$$
Задание 5
Пусть $$\frac{x}{x^2+1}=y$$. Получим: $$y+\frac{1}{y}=\frac{29}{10}\Rightarrow\frac{10y^2-29y+10}{10y}=0\Rightarrow 10y^2-29y+10=0$$
$$D=841-400=441$$
$$y_1=\frac{29+21}{20}=2,5$$
$$y_2=\frac{29-21}{20}=0,4$$
Обратная замена:
$$\frac{x}{x^2+1}=\frac{5}{2}\Leftrightarrow5x^2-2x+5=0: D<0$$ - решений нет.
$$\frac{x}{x^2+1}=\frac{2}{5}\Rightarrow2x^2-5x+2=0\Rightarrow x^2-2,5x+1=0\Rightarrow x_1+x_2=2,5$$
Задание 6
$$\log_4\cos0^{\circ}+\log_4\cos20^{\circ}+\log_4\cos40^{\circ}+\log_4\cos80^{\circ}.$$
Получим $$\log_4(\cos0^{\circ}\cos20^{\circ}\cos40^{\circ}\cos80^{\circ})$$
Учтём, что $$\cos20^{\circ}\cos40^{\circ}\cos80^{\circ}=\frac{\sin20\cos20\cos40\cos80}{\sin20}=\frac{\frac{1}{2}\sin40\cos40\cos80}{\sin20}=$$
$$=\frac{\frac{1}{4}\sin80\cos80}{\sin20}=\frac{\frac{1}{8}\sin160}{\sin20}=\frac{\frac{1}{8}\sin(180-20)}{\sin20}=\frac{\frac{1}{8}\sin20}{\sin20}=\frac{1}{8}$$
$$\cos0=1$$
Получим: $$\log_4(1\cdot\frac{1}{8})=\log_{2^2}2^{-3}=-\frac{3}{2}=-1,5$$
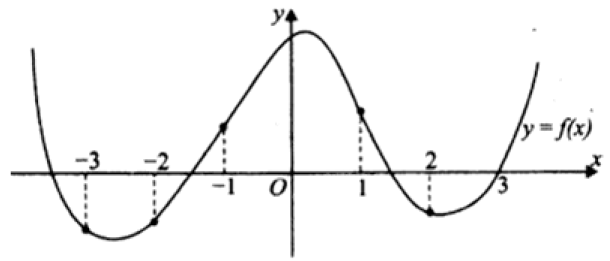
Задание 7
Производная отрицательная там, где функция убывает: -3; 1; 2. При этом, чем ближе тупой угол между касательной в эти точки и Ox, тем меньше значение производной $$\Rightarrow 1$$.
Задание 8
Очевидно, что вода будет вытекать из бака пока высота воды в баке отлична от нуля. Следовательно, чтобы найти время вытекания воды, нужно величину $$H(t)$$ приравнять к (т.к. не менее 1 метра) и из полученного уравнения найти время $$t$$:
$$at^2+bt+H_0=1$$
$$\frac{1}{500}t^2-\frac{21}{50}t+5=1$$
$$x^2-210x+2000=0$$
Решая уравнение, получаем
$$x_1=10$$
$$x_2=200$$
200 нам не подходит, значит, ответ 10
Задание 9
Чтобы из отношения $$2:3$$ получить отношение $$2:1,$$ нужно добавить четыре части меди:
$$(2 + 4):3 = 6:3 = 2:1,$$
а добавлено было 4 кг меди, следовательно, одна часть добавленной меди имела массу 1 кг.
Значит, меди было изначально 2 кг, а цинка 3 кг, всего 5 кг, а после добавления меди масса сплава стала равной 9 кг
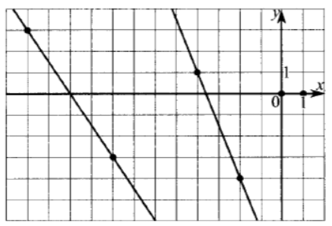
Задание 10
f(x) проходит через (-12;3) и (-8;-3).
Получим: $$\left\{\begin{matrix} 3=-12k+b\\ -3=-8k+b \end{matrix}\right.\Rightarrow\left\{\begin{matrix} 6=-4k\\ -3=-8k+b \end{matrix}\right.\Rightarrow\left\{\begin{matrix} k=-1,5\\ -15=b \end{matrix}\right.$$
$$f(x)=-1,5x-15$$
g(x) проходит через (-4;1) и (-2;-4):
$$\left\{\begin{matrix} 1=-4k+b\\ -4=-2k+b \end{matrix}\right.\Rightarrow\left\{\begin{matrix} 5=-2k\\ -4=-2k+b \end{matrix}\right.\Rightarrow\left\{\begin{matrix} k=-2,5\\ b=-9 \end{matrix}\right.$$
$$g(x)=-2,5x-9$$
Тогда: $$-1,5x-15=-2,5x-9\Rightarrow x=6\Rightarrow y=-1,5\cdot6-15=-24$$
Задание 11
1. Вычисляем производную функции:
$$y = e^{4x} - 4e^x + 8;$$
$$y' = 4e^{4x} - 4e^x = 4(e^{4x}-e^x).$$
2. Находим стационарные точки:
$$4(e^{4x} - e^x) = 0;$$
$$e^{3x + x} - e^x = 0;$$
$$e^x\cdot e^{3x} - e^x = 0;$$
$$e^x\cdot(e^{3x} - 1) = 0;$$
$$\left[\begin{matrix} e^x=0\;-\;нет\, решений\\ e^{3x}-1=0 \end{matrix}\right.$$
$$e^{3x} = 1;$$
$$3x = 0;$$
$$x = 0.$$
В точке $$x = 0$$ происходит переход от убывания к возрастанию, значит, это - точка минимума.
3. Наименьшее значение функции:
$$y = e^{4x} - 4e^x + 8;$$
$$x_{min} = 0;$$
$$y_{min} = y(0) = e^{4\cdot0}-4\cdot e^0 + 8 = 1 - 4 + 8 = 5.$$