348 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

Когда цена повысилась на 10%, то цена портфеля стала $$​6000\cdot1,1=6600​$$

Цену понизили на 10%, цена стала $$​6600\cdot0,9=5940$$

3 июля бизнесмен потратил на 200 акций $$​200\cdot140=28000​$$ рублей, далее:

4 июля он получил ​$$50\cdot135$$​ рублей

13 июля он получил ​$$150\cdot125​$$

Всего он заработал ​$$50\cdot135+150\cdot125=25500$$​ рублей

Бизнесмен потерял ​$$28000-50\cdot135-150\cdot125=2500​$$ рублей

Легче всего здесь использовать формулу Пика

​$$S=В+\frac{Г}{2}-1$$​, где ​В​ – кол-во точек внутри многоугольника, ​Г​ – кол-во точек на границе

$$​В=5, Г=6​$$

$$​S=5+3-1=7$$

Искомая вероятность будет состоять из 3-х несовместных событий:

1. Что в первое отделение доставили почту вовремя, а в остальные нет

2. Что во второе отделение доставили почту вовремя, а в остальные нет

3. Что в третье отделение доставили почту вовремя, а в остальные нет

​$$P(A+B+C)=0,95\cdot0,1\cdot0,2+0,05\cdot0,9\cdot0,2+0,05\cdot0,1\cdot0,8=0,032$$

Сделаем замену на $$3^x=a,2^x=b,a>0,b>0​$$

​$$a^3-b^3=3(a^2b-ab^2)​$$

​$$a^3-b^3=3ab(a-b)​$$

Тут сразу же вспоминается формула разности кубов

$$​(a-b)(a^2+ab+b^2)=3ab(a-b)​$$

$$​(a-b)(a^2-2ab+b^2)=0​$$

$$​(a-b)^3=0​$$

$$​a=b​$$

$$​3^x=2^x​$$

$$​(\frac{3}{2})^x=1​$$

$$​x=0$$

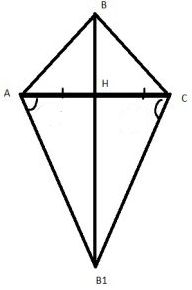
Тут можно рассмотреть несколько случаев, когда высоты треугольников лежат по одну сторону от AC и нет. Но ответ конечно же не изменится.

Рассмотрим такой рисунок, когда B и B₁ находится на противоположных сторонах (остальные случаи рассматриваются аналогично)

​$$\frac{S_{AB_1C}}{S_{ABC}}=\frac{0,5AC\cdot B_1H}{0,5AC\cdot BH}=\frac{B_1H}{BH}=3$$​

Так как AB₁C- равносторонний, то все его углы по 60, и высота – это и медиана и биссектриса

$$\tg60=\frac{B_1H}{AH}$$​

$$​B_1H=\tg60\cdot AH=\frac{\sqrt{3}}{2}AC​$$ $$(AH=0,5AC)$$

Значит, ​$$BH=\frac{AC}{2\sqrt{3}}$$​

$$​tg\angle BAH=\frac{BH}{0,5AC}=\frac{1}{\sqrt{3}}$$​

Значит, $$​\angle BAH=30​$$

и значит, наибольший угол будет $$\angle ABC=180-(30+30)=120$$

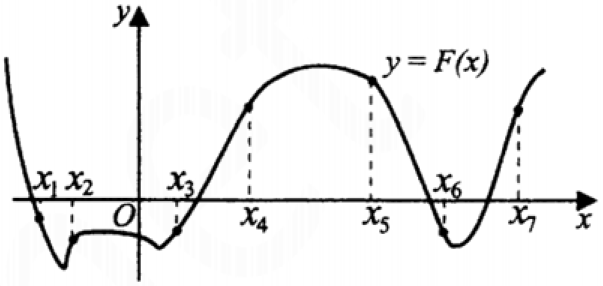
$$F'(x)=f(x)​$$

Производная будет положительна там, где функция возрастает.

$$2,3,4,7\Rightarrow 4$$ точки

Пусть $$SC$$ - большее боковое ребро

Из прямоугольного треугольника ​$$SO=\sin60\cdot6\sqrt{3}=9$$

$$\sin(90+10)=\cos10​$$

$$\cos100=\cos(90+10)=-\sin10$$

И тогда в числите будет ​$$\sin(50+10)=3\sqrt{2}$$​​, а в знаменателе ​$$sin(40-10)=0,5$$

$$2\sqrt{3}\cdot\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}=6$$

$$h_1=4,9\cdot4,5^2​$$

$$​h_2=4,9\cdot5,5^2​$$

$$​h_2-h_1=4,9\cdot(5,5^2-4,5^2)=4,9(5,5-4,5)(5,5+4,5)=49$$

Пусть ​$$x$$​ производительность первой бригады, а ​$$y$$​ производительность второй бригады

Тогда из условия (всю работу примем за 1)

​$$1=12(x+y)​$$

$$​x+y=\frac{1}{12}$$​

8 дней работая вместе ​$$8\cdot(x+y)=A_8$$​, они сделали ​$$A_8=\frac{8}{12}$$​ от всей работы

Значит осталось сделать ​$$\frac{1}{3}$$​ работы

$$7\cdot y=\frac{1}{3}​$$

Получили систему

решая ее $$​(x,y)=(\frac{1}{28},\frac{1}{21})​$$

Теперь отвечаем на вопрос задачи

$$t\cdot\frac{1}{21}=1$$​

$$​t=21​$$ – за 21 день убрала бы весь урожай 2 бригада, работая одна

Соответственно за 28 дней убрала бы весь урожай первая бригада, работая одна

$$28-21=7$$

Ограничения $$​x<2$$​ и $$​x>−4​$$

$$​y=\frac{2−x}{x+4}+6x$$​

Найдем критические точки

​$$y'=\frac{-(x+4)-(2-x)}{(x+4)^2}+6=0​$$

$$\frac{​(x+4)^2-1}{(x+4)^2}$$​

$$​x=-5​$$

$$​x=-4​$$

$$​x=3​$$

По методу интервалов ​$$x=-3​$$ – точка минимума (не забываем про ограничения)