380 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$\sqrt{x+16}-x+4=0\Leftrightarrow\sqrt{x+16}=x-4\Leftrightarrow\left\{\begin{matrix} x+16=(x-4)^2\\ x-4\geq0 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} x^2-8x+16-x-16=0\\ x\geq4 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x^2-9x=0\\ x\geq4 \end{matrix}\right.\Leftrightarrow x=9$$
Задание 2
За три года сломается $$=0,9\cdot0,9\cdot0,1=0,081$$
или (+)
За четыре года сломается $$=0,9\cdot0,9\cdot0,9\cdot0,1=0,0729$$
$$0,081+0,0729=0,1539$$ - вероятность того, что прослужит больше двух лет, но не больше 4 (3 и 4 года)
Задание 3
$$\sin M=\frac{NA}{MN}=\frac{4}{5}=0,8$$ (из прямоугольного треугольника MNA)
$$R=\frac{NP}{2\sin M}=\frac{16}{2\cdot0,8}=\frac{16}{1,6}=10$$ (из теоремы синусов)
Задание 4
Учтём, что $$34-24\sqrt{2}=16-2\cdot4\cdot3\sqrt{2}+(3\sqrt{2})^2=(4-3\sqrt{2})^2.$$
Тогда $$\sqrt{34-24\sqrt{2}}=\sqrt{(4-3\sqrt{2})^2}=|4-3\sqrt{2}|=3\sqrt{2}-4$$
Получим: $$(4-3\sqrt{2})^2+8(3\sqrt{2}-4)=34-24\sqrt{2}+24\sqrt{2}-32=2$$
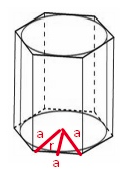
Задание 5
По теореме Пифагора:
$$a=\sqrt{r^2+\frac{a^2}{4}}$$
$$\frac{3}{4}a^2=r^2$$
$$a=\frac{2r}{\sqrt{3}}$$
$$a=2$$
$$S_{бок}=6\cdot a\cdot h=6\cdot2\cdot2=24$$
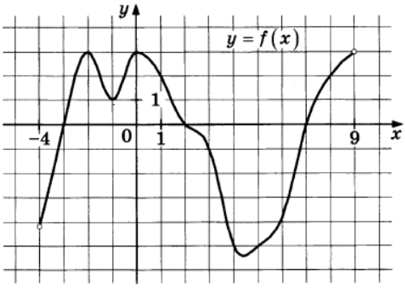
Задание 6
$$f'(x)>0$$ если $$f(x)$$ возрастает:
$$(-4;-2)$$: 1 точка -3
$$(-1;0)$$: 0 точек
$$(\approx4,4;9)$$: 4 точки: 5; 6; 7; 8.
Всего 5 целых значений.
Задание 7
$$140=\frac{1260\cdot10}{2\cdot18\cdot S}\Rightarrow$$
$$\Rightarrow S=\frac{1260\cdot10}{140\cdot2\cdot18}=2,5$$
Задание 8
Пусть $$V$$ - скорость движения вверх по реке, тогда $$1,04V$$ - по озеру.
Пусть $$t$$ - время по реке, тогда $$1,15t$$ - по озеру.
Получим:
$$S_1=Vt$$ - расстояние по реке
$$S_2=1,04V\cdot1,15t=1,196Vt=1,196S_1$$ - по озеру $$\Rightarrow$$ на $$19,6\%$$
Задание 9
График проходит через $$(-1;1)$$ и $$(1;2).$$ Тогда:
$$\left\{\begin{matrix} 1=\log_a(-1+b)\\ 2=\log_a(1+b) \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 1=\log_a(b-1)\\ \frac{2}{1}=\frac{\log_a(b+1)}{\log_a(b-1)} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=b-1\\ 2=\log_{b-1}(b+1) \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} a=b-1\\ (b-1)^2=b+1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a=b-1\\ b=0;3 \end{matrix}\right.$$
$$b=0$$ - не подходит, так как $$b-1>0\Rightarrow b=3;a=2.$$
Получим:
$$y=\log_2(x+3)$$
$$f(29)=\log_2(29+3)=5$$
Задание 10
$$P(B|A)=\frac{P(AB)}{P(A)}$$
A – не выпало ни на одной 4
B – выпало в сумме 12
$$P(A)=\frac{25}{36}$$
$$P(AB)=\frac{1}{36}$$
$$P(B|A)=\frac{1}{25}=0,04$$
Задание 11
$$f'(x)=\sqrt{3}-\frac{\sqrt{3}}{\cos^2x}$$
Так как $$\cos^2x\in[0;1],$$ то $$\frac{\sqrt{3}}{\cos^2x}\geq1.$$
$$\Rightarrow f'(x)\geq0\Rightarrow f(x)$$ возрастает на всём $$D(f)$$
$$\Rightarrow f_{min}=f(-\frac{\pi}{3})=\sqrt{3}\cdot(-\frac{\pi}{3})-\sqrt{3}\ctg(-\frac{\pi}{3})+\frac{\pi\sqrt{3}}{3}=-\sqrt{3}\cdot(-\frac{\sqrt{3}}{3})=1$$