351 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
Задание 1
Пусть $$x$$ – это во сколько возрастает цена
Тогда можно составить уравнения исходя из условия
$$2560000x^2=4000000$$
$$x=1,25$$
Значит, $$25\%$$
Задание 2
$$10-3=7$$
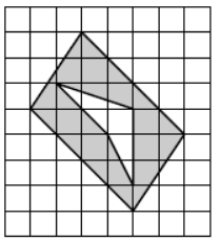
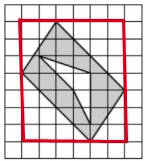
Задание 3
Из площади большого прямоугольника вычитаем площадь 4-х прямоугольных треугольник (заметим, что симметричные треугольники равны по площади) и внутренней фигуры (по формуле Пика (S=B+Г/2-1))
$$S=6\cdot7-2\cdot0,5\cdot4\cdot4-2\cdot0,5\cdot3\cdot2-(1+\frac{7}{2}-1)=16,5$$
Задание 4
(Автор задачи Николай Журавлев)
Пусть $$P(A)$$ – вероятность, что справились участник А справился с задачей, $$P(B)$$ – участник Б справился с задачей
и $$P(\overline{A}),P(\overline{B})$$ – вероятности, что не справятся с задачей
Тогда из условия можно составить два уравнения
$$P(B)P(\overline{A})+P(B)\cdot P(\overline{A})\cdot P(\overline{B})=0,32$$ (не забываем, что у участника Б изначально 2 попытки, а у А только одна)
$$P(\overline{A})\cdot P(B)=0,2$$ – Пусть $$P(\overline{A})\cdot P(B)=x$$ – это подставляем в первое уравнение
$$x+P(\overline{B})x=0,32$$
$$P(\overline{B})=\frac{0,12}{x}=\frac{0,12}{0,2}=0,6$$
Если участник А после этого истратит попытку неудачно, то тогда участнику Б остается справиться с заданием
$$P(B)=1-P(\overline{B})=0,4$$
Задание 5
Очевидная замена $$x+\frac{1}{x}=t$$
$$t^2-4,5t+5=0$$
$$t=2$$
$$t=2,5$$
$$x+\frac{1}{x}=2$$
$$x+\frac{1}{x}=2,5,\quad x\neq0$$
$$x^2-2x+1=0$$
$$x^2-2,5x+1=0$$
$$x=1$$
$$x=0,5$$ и $$x=2$$
Произведение корней равно 1
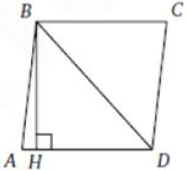
Задание 6
По теореме Пифагора $$BH=\sqrt{80}$$ и тогда по теореме Пифагора $$BD=12$$
Задание 7
По геометрическому смыслу производной можно составить уравнение
$$3x^2-12x+8=-4$$
Откуда $$x=2$$
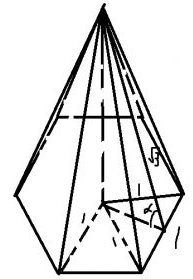
Задание 8
Высоту в основании правильного треугольника легко найти – это $$1\cdot\frac{3}{\sqrt{2}}$$
$$\cos\alpha=\frac{1\cdot\frac{\sqrt{3}}{2}}{\sqrt{3}}=0,5$$, значит, угол $$60^{\circ}$$
Задание 9
$$\log_2(4\sqrt{2})=\log_2 2^{2+0,5}=2,5$$
$$\lg(10\cdot\frac{5}{2})=\lg25$$
$$\frac{\lg5}{\lg25}=\log_{25}5=0,5$$
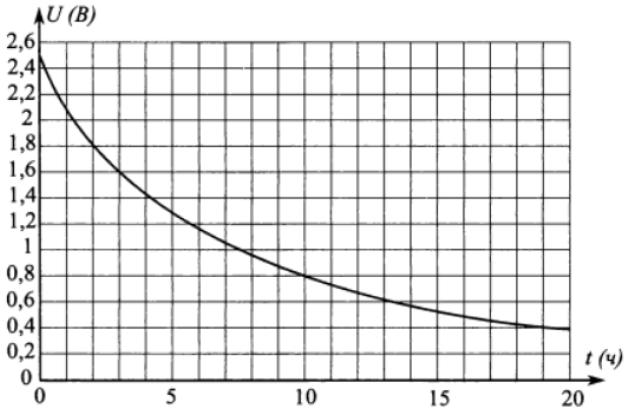
Задание 10
$$H(t) = H_0-\sqrt{2gH_0}\cdot kt+\frac{g}{2}k^2t^2$$
где $$t$$ - время (в секундах), прошедшее с момента открытия крана, $$H_0 = 20$$ м - начальная высота столба воды, $$k = \frac{1}{400}$$ отношение площадей поперечных сечений крана и бака, $$g$$ - ускорение свободного падения (считайте, что $$g = 10$$ м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма?$$V_0=S_{осн}\cdot H_0$$ - начальный объем
$$V=S_{осн}\cdot H(t_1)=\frac{1}{4}S_{осн}\cdot H_0$$
$$H(t_1)=5$$
$$5=20-\sqrt{20\cdot20}\cdot\frac{1}{400}t_1+5\frac{1}{400^2}t^2_1$$
$$t_1=400$$
$$t_1=1200$$ – это не подходит, т.к. после 400 секунд объем будет меньше $$\frac{1}{4}$$
Задание 11
По условию $$V_1=2V_2$$
Из условия
$$tV_1=(t+1)0,5V_1$$
Пусть встреча произошла через время $$t_1$$
$$t_1V_1+t_10,5V_1=S$$
Из первого уравнения
$$t=1$$
$$S=V_1$$ – подставим во второе
$$t_1=\frac{2}{3}$$ часа или 40 минут
Теперь, если бы они ехали с одинаковыми скоростями.
$$tV_1+tV_1=V_1$$
Значит, $$t=0,5$$ часа или 30 минут
$$40-30=10$$ минут
Задание 12
Найдем критические точки.
$$\frac{7}{π}+\frac{4}{3}\sin x=0$$
$$\sin x=-\frac{21}{4}π$$ - нет решений, т.к. область значений синуса [-1;1].
Значит, наименьшее значение достигается на границах.
В $$x=-\frac{2π}{3}$$ – будет достигаться наименьшее значения.
$$y(-\frac{2π}{3})=−7$$