247 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 247 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №247 (alexlarin.com)
Решаем ЕГЭ 247 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №247 (alexlarin.com)
Задание 1
В кафе действует следующее правило: на ту часть заказа, которая превышает 1000 рублей, действует скидка 25%. После игры в футбол студенческая компания из 20 человек сделала в кафе заказ на 3400 рублей. Все платят поровну. Сколько рублей заплатит каждый?
Задание 2
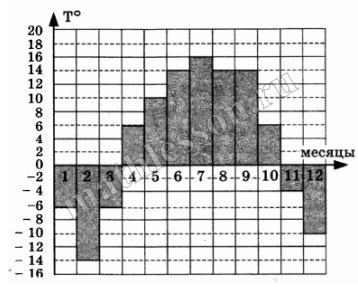
На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей температурами в 1994 году. Ответ дайте в градусах Цельсия.
Задание 3
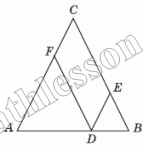
Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр параллелограмма, ограниченного этими прямыми и боковыми сторонами данного треугольника.
Задание 4
Бросают два игральных кубика. Найдите вероятность того, что произведение выпавших очков больше или равно 10. Ответ округлите до сотых.
Рассмотрим возможные произведения (по центру будут произведение выпавших чисел)
| Первый кубик/Второй кубик (число) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 |
Количество произведений $$\geq 10$$: 19 (выделены жирным шрифтом)
Общее количество - 36
$$P=\frac{19}{36}\approx 0,527\approx 0,53$$
Задание 5
Найдите корень уравнения: $$\sqrt{4x^{2}-4x+2}=\sqrt{1+x-2x^{2}}$$ . Если уравнение имеет более одного корня, укажите больший из них.
Область определения D:
$$\left\{\begin{matrix}4x^{2}-4x+2\geq 0\\1+x-2x^{2}\geq 0\end{matrix}\right.$$
Возведем обе части в квадрат :
$$4x^{2}-4x+1=0\Leftrightarrow$$$$6x^{2}-5x+1=0$$
$$D=25-24=1$$
$$x_{1}=\frac{5+1}{12}=0,5$$
$$x_{2}=\frac{5-1}{12}=\frac{1}{3}$$
Оба корня попадают в D, наибольший равен 0,5
Задание 6
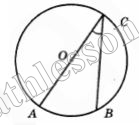
$$\cup AB=\frac{1}{5}*260=72$$ $$\angle ACB=\frac{1}{2}\cup AB=36$$(вписанный)
Задание 7
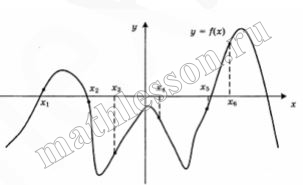
На рисунке изображен график функции $$y=f(x)$$. Найдите среди точек x1,x2,...,x6 те точки, в которых производная функции $$y=f(x)$$ отрицательна. В ответ запишите количество найденных точек.
f'<0 если f(x)-убывает : $$x_{2};x_{4}$$ - две точки
Задание 8
Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Пусть $$V_{1}$$ - объем описанного, $$V_{2}$$ - вписанного. Т.к. высота у них одна, то $$\frac{V_{1}}{V_{2}}=\frac{S_{1}}{S_{2}}$$. Пусть $$a$$-сторона основания (квадрата)
Из квадрата : $$\frac{1}{2}a=R_{2}$$
$$\sqrt{(\frac{a}{2})^{2}+(\frac{a}{2})^{2}}=$$$$\frac{a}{\sqrt{2}}=R_{1}$$
$$\frac{S_{1}}{S_{2}}=(\frac{R_{1}}{R_{2}})^{2}=$$$$(\frac{a}{\sqrt{2}}*\frac{2}{a})^{2}=2$$
Задание 9
Найдите $$\frac{p(b)}{p(\frac{1}{b})}$$, если $$p(b)=(b-\frac{7}{b})(-7b+\frac{1}{b})$$ при $$b\neq0$$
$$p(\frac{1}{b})=$$$$(\frac{1}{b}-\frac{2}{1})(-7*\frac{1}{6}+\frac{1}{\frac{1}{6}})=$$$$(\frac{1}{6}-7b)(-\frac{7}{b}+b)=p(b)$$
$$\frac{p(b)}{p(\frac{1}{b})}=\frac{p(b)}{p(b)}=1$$
Задание 10
$$y(60)=0,0041*60^{2}-0,71*60+34=$$$$0,41*36-7,1+34=$$$$14,76-42,6+34=6,16$$
Задание 11
Из города A в город B одновременно выехали два автомобиля: первый со скоростью 80 км/ч, а второй—со скоростью 60 км/ч. Через полчаса следом за ними выехал третий автомобиль. Найдите скорость третьего автомобиля, если известно, что с момента, когда он догнал второй автомобиль, до момента, когда он догнал первый автомобиль, прошёл 1 час 15 минут. Ответ дайте в км/ч.
За полчаса первый проедет 40 км., второй 30 км. Тогда время , за которое догонит третий второго: $$t_{2}=\frac{30}{x-60}$$, первого: $$t_{1}=\frac{40}{x-80}$$, где x-км\ч скорость третьего
$$\frac{40}{x-80}-\frac{30}{x-60}=$$$$1\frac{15}{60}=\frac{5}{4}| : \frac{5}{4}$$
$$\frac{32}{x-80}-\frac{24}{x-60}=1\Leftrightarrow$$$$32x-60*32-24x+24*80=x^{2}-140x+4800\Leftrightarrow$$$$x^{2}-140x -8x+4800=0\Leftrightarrow$$$$x^{2}-148x+4800=0\Leftrightarrow$$
D=21904-19200=2704
$$x_{1}=\frac{148+52}{2}=48<80$$
$$x_{2}=\frac{148+52}{2}=100$$ км/ч - скорость 3го
Задание 12
Найдите наименьшее на отрезке [1;6] значение функции $$y=7|x-3|-2|x+5|-|4x-3|+5$$
На промежутке [1;6] x+5>0 4x-3>0, тогда: $$y=7\left | x-3 \right |-2x-10-4x+3+5=$$$$7\left | x-3 \right |-6x-2$$
Вершина полученного графика будет находиться в точке, где подмодульное выражение равно 0, то есть $$x=3\Rightarrow$$ $$y_{min}=y(3)$$
$$y(3)=7\left | 3-3 \right |-6*3-2=-20$$
Задание 13
A) Область определения D(x):
$$\left\{\begin{matrix}2\cos x-1\neq 0\\2 \cos ^{2}x-\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\cos x=\frac{1}{2}\\\cos x\neq 0\end{matrix}\right.$$
$$\frac{2\cos x-3}{2\cos x-1}+\frac{1}{\cos x(2 \cos x-1)}=0$$
Приведем к общему знаменателю и приравняем числитель к нулю:
$$2 \cos^{2}x-3\cos x+1=0$$
Пусть $$\cos x=t \in [-1 ;1]$$
$$2t^{2}-3t+1=0$$
$$D=9-8=1$$
$$t_{1}=\frac{3+1}{4}=1$$
$$t_{2}=\frac{3-1}{4}=\frac{1}{2}$$
Тогда : $$\left\{\begin{matrix}\cos x=1\\\cos x=\frac{1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=2\pi n , n \in Z\\\notin D(x)\end{matrix}\right.$$
Б) На данном промежутке при n=-2 получаем $$x=-4\pi$$
Задание 14
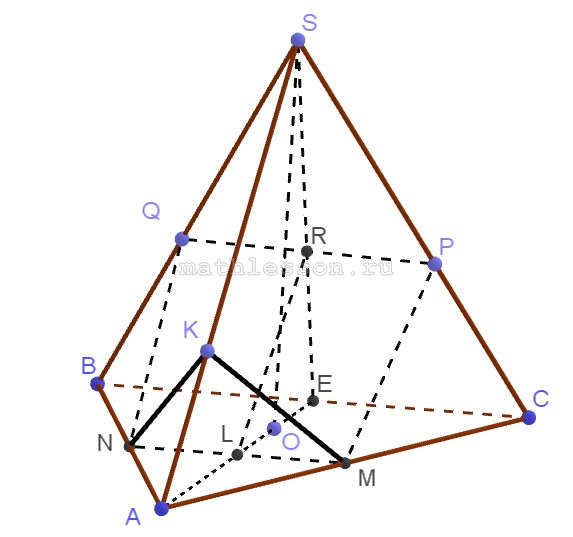
Через середину ребра АС правильной треугольной пирамиды SABC (S – вершина) проведены плоскости $$\alpha$$ и $$\beta$$ , каждая из которых образует угол 300 с плоскостью АВС. Сечения пирамиды этими плоскостями имеют общую сторону длины 1, лежащую в грани АВС, а плоскость $$\alpha$$ перпендикулярна ребру SA.
A) 1) AE- медиана $$\Rightarrow AE\perp NM\Rightarrow$$ $$NM\perp AS$$(теорема о трёх перпендикулярах )$$\Rightarrow (MNK)=\alpha$$
2) $$S_{MNC}=S_{NMA}*\cos30$$
$$MN=1\Rightarrow$$ $$CB=2\Rightarrow$$ $$S_{AMN}=\frac{1}{4}*S_{ABC}=$$$$\frac{1}{4}*\frac{1}{2}*2*2*\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$$
$$S_{MNK}=\frac{\sqrt{3}}{4}*\frac{\sqrt{3}}{2}=\frac{3}{8}$$
Б) 1) $$\beta \cap ABC=MN\Rightarrow$$ т.к. $$(BSK)\cap ABC=BC$$, то $$MN\left | \right |QP\Rightarrow QPMN$$ - равнобокая трапеция
2) $$\angle SAE=90-30=60(\Delta KLA)$$
$$\Delta ABC:AE=AC*\sin 60=$$$$\frac{\sqrt{3}}{2}*2=\sqrt{3}$$
$$AD=\frac{2}{3}AE=\frac{2\sqrt{3}}{3}$$, $$\Delta ASO:AS=\frac{AO}{\cos 60}=$$ $$\frac{2\sqrt{3}}{3}*2=\frac{4\sqrt{3}}{3}$$
3) $$\angle LRE=30$$, пусть AF –биссектриса $$SAE\Rightarrow AF\left | \right |LR$$, $$LR=\frac{1}{2}AF(\Delta AFE)$$
$$AF=\frac{2*AE*AS}{AE+AS}*\cos \frac{SAE}{2}=$$$$\frac{2\sqrt{3}*\frac{4\sqrt{3}}{3}}{\sqrt{3}+\frac{4\sqrt{3}}{3}}*\frac{\sqrt{3}}{2}=$$$$\frac{12}{7}\Rightarrow LR=\frac{6}{7}$$
4) По свойству биссектрисы: $$\frac{SF}{FE}=\frac{SA}{AE}=\frac{4}{3}$$
$$RE=FR=\frac{1}{2}FE=$$$$\frac{1}{2}*\frac{3}{7}AE=$$$$\frac{3}{14}SE$$
$$PQ=\frac{11}{12}BC=\frac{11}{7}\Rightarrow$$ $$S_{\beta}=\frac{1+\frac{11}{7}}{2}*\frac{6}{7}=\frac{54}{49}$$
Задание 15
Решите неравенство: $$\log_{x}\frac{x+1}{12x}> 2\log_{\frac{x+1}{12x}} x$$
Область определения D(x):
$$\left\{\begin{matrix}x>0\\x\neq 1\\\frac{x+1}{12x}>0\\\frac{x+1}{12}>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>0\\x\neq 1\\x+1>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>0\\x\neq 1\\x>-1\end{matrix}\right.\Leftrightarrow$$ $$x\in (0;1)\cup (1;+\infty )$$
Разложим данные логарифмы:
$$\log_{x}(x+1)-(\log_{x}12+\log_{x}x)-\frac{2}{\log_{x}\frac{x+1}{12}}>0$$
$$\log_{x}(x+1)-\log_{x}12-1-\frac{2}{\log_{x}}\frac{x+1}{12}>0$$
$$\log_{x}\frac{x+1}{12}-\frac{2}{\log\frac{x+1}{12}}-1>0$$
$$\frac{\log_{x}^{2}\frac{+1}{12}-\log_{x}\frac{x+1}{12}-2}{\log_{x}\frac{x+1}{12}}>0$$
$$\frac{(\log_{x}\frac{+1}{12}-2)(\log_{x}\frac{x+1}{12}-1)}{\log_{x}\frac{x+1}{12}}>0$$
Воспользуемся методом рационализации:
$$\frac{(x-1)(x+1-12x^{2})(x^{2}+x-12)}{(x+1-12)}>0$$
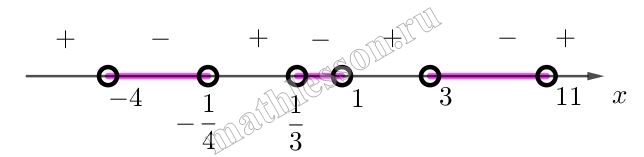
$$\frac{(x-1)(x-\frac{1}{3})(x+\frac{1}{4})(x-2)(x+4)}{x-11}<0$$
С учетом области определения:
$$x \in (\frac{1}{3};1)\cup (3 ;11)$$
Задание 16
В треугольнике АВС угол С тупой, а точка D выбрана на продолжении АВ за точку В так, что $$\angle ACD=135$$ точка D' симметрична точке D относительно прямой ВС, точка D'' симметрична точке D’ относительно прямой АС и лежит на прямой ВС. Известно, что $$\sqrt{3}BC=CD''$$, AC=6.
A) 1) Пусть $$\angle {D}'CO=\alpha$$ .Т.к. $${D}'Q=QD$$, CQ-общая и $$\angle {D}'QC=90$$, то $$\Delta C{D}'Q=\Delta CQD$$ и $$\angle QCD=\alpha$$
2) из $$\Delta ACD :\angle ACB=135-\alpha$$
$$\angle AC{D}'=135-2\alpha =\angle {D}''CA$$(аналогично п.1)
$$\angle {D}''CA+ACQ=180$$
$$135-2\alpha +135-\alpha =180$$
$$3\alpha =90\Leftrightarrow$$ $$\alpha=30$$
3) Пусть $${D}''C=x$$, тогда $$C{D}'=x=CD$$.Т.к. $$\angle {D}'CD=2\alpha=60$$ и $$C{D}'=CD$$, $$\Delta C{D}'D$$-равносторонний .Тогда $$CQ=C{D}'\sin 60=\frac{\sqrt{3x}}{2}$$
4) $$BC=\frac{C{D}''}{\sqrt{3}}=\frac{\sqrt{3}x}{3}$$.Тогда $$BQ=CQ-CB=$$$$\frac{\sqrt{3}x}{2}-\frac{\sqrt{3}x}{3}=\frac{\sqrt{3}x}{6}$$, $$\frac{CB}{BQ}=\frac{\sqrt{3}x}{3}:\frac{\sqrt{3}x}{6}=2:1$$
а т.к. $$CQ\perp DB$$, то CQ- медиана, тогда B-точка пересечения медиан $$\Rightarrow CN\perp C{D}'$$ и $$\angle BDC=\angle BD{D}'\Rightarrow$$ $$\Delta CBD$$-равнобедренный.
Б) 1) $$\angle ACB=135-\alpha=105$$ , $$\angle ABC=180-120=60.$$
По т. Синусов из $$\Delta ACB$$: $$\frac{AC}{\sin \beta }=\frac{OB}{\sin \alpha }\Leftrightarrow$$ $$CB=\frac{6*\sin 15}{\sin 60}=4\sqrt{3}\sin 15$$
2) $$S_{ABC}=\frac{1}{2}AC*CB*\sin C=$$$$\frac{1}{2}*6*4\sqrt{3}\sin 15 *\sin 105=$$$$12\sqrt{3}*\sin 15*\cos 15=$$$$12\sqrt{3}*\frac{1}{2}*\sin 30=3\sqrt{3}$$
Задание 17
В пряничный цех поступил заказ на изготовление партии сувенирных пряников трех видов: с клубничной начинкой, с вишневой и с шоколадной. Цена пряников с клубничной и вишневой начинкой одинакова, первых заказали на сумму 4000 руб, вторых – 60 штук. Пряники с шоколадной начинкой стоят 150 руб за штуку, их заказали столько же, сколько пряников с вишневой и клубничной начинками вместе. Какова наименьшая стоимость всего заказа? При какой цене на пряники с фруктовой начинкой она достигается?
Пусть x-цена пряников с клубникой и вишневой начинкой. Пусть y-количество пряников с клубникой, тогда цена одного: $$x=\frac{4000}{y}(1)$$. Общее количество с клубникой и вишней $$(y+60)$$. Общая их цена : $$(y+60)*x$$
Общая цена с шоколадом : $$(y+60)*150$$. Итого: $$S=(y+60)*x+(y+60)*150$$
С учетом (1): $$y=\frac{4000}{x}$$
$$S=(\frac{4000}{x}+60)x+(\frac{4000}{x}+60)*150\rightarrow min$$
$$S=4000+60x+\frac{600000}{x}+9000=$$$$60x+\frac{600000}{x}+13000$$
$${S}'=60-\frac{600000}{x^{2}}=0$$
$$x^{2}=\frac{600000}{60}=10000$$
$$x=\pm 100$$
То есть $$x_{min}=100$$
$$S=4000+60*100+\frac{600000}{100}+9000=25000$$
Задание 18
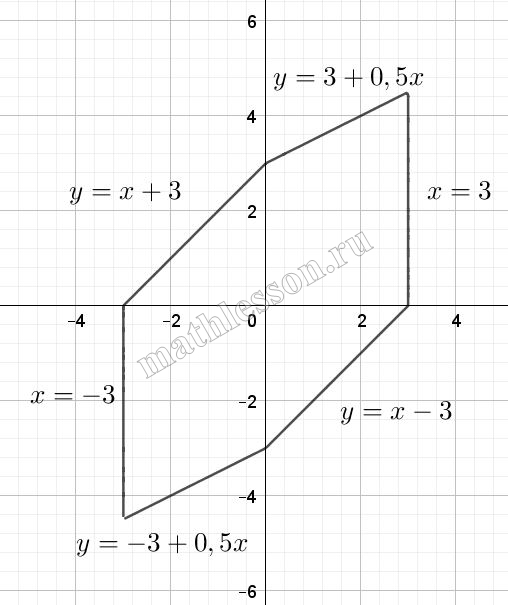
Найдите все значения a, при которых система уравнений $$\left\{\begin{matrix}|x|+|y|+|2y-3x|=12\\ x^{2}+y^{2}=a \end{matrix}\right.$$ имеет ровно две действительные пары решений
$$\left\{\begin{matrix}\left | x \right |+2\left | y \right |+\left | 2y-3x \right | =12=f\\x^{2}+y^{2}=a=g\end{matrix}\right.$$
g - окружность с центром в начале координат и радиуса $$\sqrt{a}\Rightarrow a>0$$
Рассмотрим график f:
При $$2y-3x\geq 0\Leftrightarrow$$ $$y\geq 1,5 x$$ получили $$\left | x \right |+2\left | y \right |+ 2y-3x =12$$
В данном случае будет 3 части плоскости:
1)$$\left\{\begin{matrix}x\geq 0\\y\geq 0\end{matrix}\right.\Rightarrow$$ $$x+2y+2y-3x=12\Leftrightarrow$$ $$y=3+0,5x$$
2)$$\left\{\begin{matrix}x<0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$-x+2y+2y-3x=12\Leftrightarrow$$ $$y=3+x$$
3)$$\left\{\begin{matrix}x<0\\y<0\end{matrix}\right.\Leftrightarrow -x-2y+2y-3x=12\Rightarrow x=-3$$
При $$2y-3x<0\Leftrightarrow y<1,5x$$ получим так же 3 части плоскости:
1)$$\left\{\begin{matrix}x\geq 0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$x+y-2y+3x=12\Leftrightarrow x=3$$
2)$$\left\{\begin{matrix}x\geq 0\\y<0\end{matrix}\right.\Leftrightarrow$$ $$x-y-2y+3x=12\Leftrightarrow y=-3+x$$
3)$$\left\{\begin{matrix}x<0\\y<0\end{matrix}\right.\Leftrightarrow$$ $$-x-y-2y+3x=12\Leftrightarrow y=x-3$$
Построим график данной функции .
Очевидно , что 2 точки будет если пройдет через (C) и если касается в (B)
Найдем координаты (C) :$$y=3+0,5=4,5$$.
Тогда $$OC=r_{1}^{2}=a=3^{2}+4,5^{2}=29,25$$. Найдем $$OB=r_{2}^{2}=a=1,5^{2}+1,5^{2}=4,5.$$
Задание 19
А)Можно ли в выражении $$\frac{1}{2}*\frac{1}{3}*\frac{1}{4}*\frac{1}{5}*\frac{1}{6}*\frac{1}{7}*\frac{1}{8}$$ вместо всех знаков * так расставить знаки «+» и «‐», чтобы модуль этого выражения стал меньше $$\frac{1}{8}$$ ?
Б) Можно ли в выражении $$\frac{1}{2}*\frac{1}{3}*\frac{1}{4}*\frac{1}{5}*\frac{1}{6}*\frac{1}{7}*\frac{1}{8}$$ вместо всех знаков * так расставить знаки «+» и «‐», чтобы модуль этого выражения стал меньше $$\frac{1}{500}$$ ?
В) Какое наименьшее значение может принимать выражение $$|\frac{1}{2}*\frac{1}{3}*\frac{1}{4}*\frac{1}{5}*\frac{1}{6}*\frac{1}{7}*\frac{1}{8}|$$ , если разными способами заменять каждый из знаков * заменять знаками «+» и «‐»?
A) да, $$\frac{1}{2}-\frac{1}{3}-\frac{1}{4}+\frac{1}{5}+\frac{1}{6}-\frac{1}{7}-\frac{1}{8}$$
Б) Приведем к общему знаменателю и найдем наибольшую сумму: $$\frac{4*3*5*7+8*5*7+2*3*5*7+8*3*7+4*5*7+8*3*5+3*5*7}{840}=$$$$\frac{420+280+210+168+140+120+105}{840}=\frac{1443}{840}$$
Очевидно, что $$\frac{1}{840}<\frac{1}{500}$$, $$\frac{2}{840}>\frac{1}{500}$$
То есть в числителе обязательно должна быть 1. С учетом того, что общая сумма 1443: пусть сумма m , разность - n.
Тогда $$\left | m-n \right |=1$$. Но из всех представленных чисел все, кроме 168 и 105 оканчиваются на 0, следовательно, их сумма/разность тоже на 0. $$\left | 168 \pm 105 \right |$$ оканчивается на 3 , то есть min значение в числителе $$\geq 3$$. Значит, не может быть.
B) $$1443=722+721$$. Т.е. идеальная сумма/разность для min была бы $$\left | 722-721 \right |$$. Но мы доказали , что $$\left | m \pm n \right |\geq 3$$. Т.е. $$\left\{\begin{matrix}m+n=1443\\m-n=3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2m=1446\\n=m*3\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}m=723\\n=720\end{matrix}\right.$$
Число 720 сумма тех, что оканчиваются на 0 . Но из {420;480;210;140;120} сумму в 720 не получить.
Пусть теперь: $$\left\{\begin{matrix}m+n=1443\\m-n=13\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}m=728\\n=715\end{matrix}\right.$$
$$715=105+120+210+280$$, т.е. $$min=\frac{13}{840}$$