350 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

Пусть у Сергея было ​$$S$$​ рублей и тетрадь стоит $$x$$​ рублей. Тогда составим систему

$$\left\{\begin{matrix} S-15x=7\\ S-20x=-8 \end{matrix}\right.$$

Вычтем из 2-го первое

$$​-5x=-15​$$

$$​x=3​$$

​$$S=7+15x=7+15\cdot3=52$$

$$V=\frac{S}{t}$$​

Движение как видно из графика – равномерное

$$​V=\tg\alpha=\frac{35}{40}$$​ км/мин. Переводим в часы ​$$V=\frac{35\cdot60}{40}=52,5$$

Можно решать аналитически и с помощью рисунка. Но так как рисовать не очень удобно, то решим аналитически

Найдем расстояние между центрами двух окружностей

$$​l=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=\sqrt{(-9-15)^2+(-6-12)^2}=30​$$

Но это мы нашли расстояние между центрами! По условию сказано, что она касается второй окружности с радиусом 1. Значит наименьший радиус первой будут ​$$R=30−1=29$$

Переберем все положительные исходы

$$​11,13,15​$$

$$​22,24,26​$$

$$​31,33,35​$$

​$$42,44,46​$$

Всего исходов $$6\cdot6=36$$

$$​P=\frac{12}{36}\approx0,33$$

Сделаем замену на ​$$x+\frac{1}{x}=t​$$

Нужно как-то выразить $$x^5+\frac{1}{x^5}$$​ через $$t$$

Рассмотрим такое выражение $$​(x^3+\frac{1}{x^3})(x^2+\frac{1}{x^2})=x^5+\frac{1}{x^5}+x+\frac{1}{x}=x^5+\frac{1}{x^5}+t​$$

​$$x^2+\frac{1}{x^2}=(x+\frac{1}{x})^2−2=t^2−2​$$

$$​(x^2+\frac{1}{x^2})(x+\frac{1}{x})=x^3+\frac{1}{x^3}+x+\frac{1}{x}​$$

Т.е. $$x^3+\frac{1}{x^3}=t(t^2−3)​$$

Значит,

$$x^5+\frac{1}{x^5}=t(t^2−3)(t^2−2)−t​$$

$$​t(t^2−3)(t^2−2)−t=\frac{205}{16}t​, ​t\neq0​$$

$$​(t^2−3)(t^2−2)=\frac{205}{16}+1​$$

Обычное биквадратное уравнение

$$​t=−\frac{5}{2},\frac{5}{2}$$​

Делаем обратную замену

$$x+\frac{1}{x}=-\frac{5}{2}$$

$$x=-2$$ и $$x=-\frac{1}{2}$$

$$x+\frac{1}{x}=\frac{5}{2}$$

$$x=2$$ и $$x=\frac{1}{2}$$

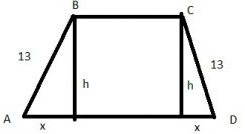
$$S=\frac{BC+AD}{2}\cdot h​$$

$$​AD=20$$​ 

$$​BC=20−2x​$$

$$\frac{​20−2x+20}{2}h=180$$​ – по условию

По теореме Пифагора

$$x^2+h^2=13^2$$​

Получили систему из 2-х неизвестных, решая ее любым способом, получаем:

$$​h=12​\quad ​x=5$$

$$BC=20-2\cdot5=10$$

Функция будет принимать наименьшее значение там, где производная меняет знак с – на +

Таких точек целых две $$x=-2; 5$$. Чисто интуитивно понятно, что в точке $$x=-2$$ значение функции будет наименьшим, т.к. функция долго убывала. Но это можно доказать “чисто”, используя известный вам интеграл

Из графика

$$​\int^3_{-2}f'(x)dx>\int^5_3f'(x)dx​$$

$$​f(3)−f(−2)>f(5)−f(3)​$$

$$​f(5)>f(−2)$$

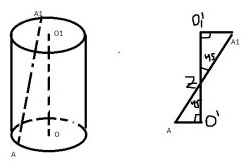
Построим параллельную прямую оси цилиндра $$O'O_1'$$, получаем, что треугольники $$AO'Z$$ и $$A_1O_1'Z$$ равны (они оба прямоугольные, равнобедренные треугольники)

Значит $$O_1'Z=O'Z$$, значит, $$O_1Z=O'Z=\frac{r}{2}$$, $$O_1A_1=\frac{r}{2}$$ и $$O'A=\frac{r}{2}$$ (равнобедренные треугольники)

По теореме Пифагора $$​AZ=\sqrt{2}\frac{r}{2}$$​

$$​AA_1=2AZ=\sqrt{2}r=7\sqrt{2}$$

$$​r=7$$

По условию ​$$\tg x=\frac{8}{15}$$​ (x - это некий угол)

Из основного тригонометрического тождества

$$​1+\tg^2x=\frac{1}{\cos^2x}$$​

$$\cos^2x=\frac{1}{\tg^2x+1}=\frac{225}{289}$$​

​$$\cos x=\frac{15}{17}$$​ данный угол лежит в первой четверти

Значит, $$\sin(0)=0$$

$$pV^a\geq32p(\frac{V}{16})^a$$​

$$V^a\geq32\cdot\frac{V^a}{16^a}$$​

$$​2^{4a}\geq2^5​$$

$$a\geq1,25​$$

Пусть $$t$$ – время встречи с первым

$$\left\{\begin{matrix} ​0,5V_в=S​\\ ​tV_в+tV_п=S​\\ 1,2V_в=2tV_п+1,2V_п​ \end{matrix}\right.$$

Решая систему, получаем $$t=0,3$$ ч

Рассмотрим два случая.

1) $$​−2\leq x<−1$$​

​$$y=5x^3+x^2+x​$$

Найдем критические точки:

$$​15x^2+2x+1=0​$$ – нет решений

(Возможно наименьшее значение будет на границах)

2) $$​−1\leq x\leq0​$$

$$​y=5x^3−x^2−1$$​

Найдем критические точки:

​$$15x^2−2x−1=0​$$

$$​x=−\frac{1}{5}​$$

$$​x=\frac{1}{3}$$​ – точка локального минимума

Но не забываем проверить границы, при проверке наименьшее значение будет в точке $$​x=−2$$

$$y(-2)=-38$$