340 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.
Больше разборов на моем ютуб-канале
Задание 1
Запишем, что мы знаем
$$V=2M$$
$$C>M, C<B$$
Или
$$V=2M$$
$$C>M, C<2M$$
Тут нужно подбирать
Пусть Маша съела 10 конфет $$(M=10)$$, значит $$V=20$$, но это уже перебор, т.к. всего конфет $$27$$
Уменьшаем
Пусть $$M=9$$, значит $$V=18$$, значит $$C=27−9−18=0$$, т.е. Саша ничего не съел – этот вариант не подходит под условия
$$M=8, V=16, C=27−16−8=3<9$$ – это не подходит
$$M=7, V=14, C=6<7$$ – не подходит
$$M=6, V=12, C=9>6$$ и меньше $$12$$ – это нас устраивает
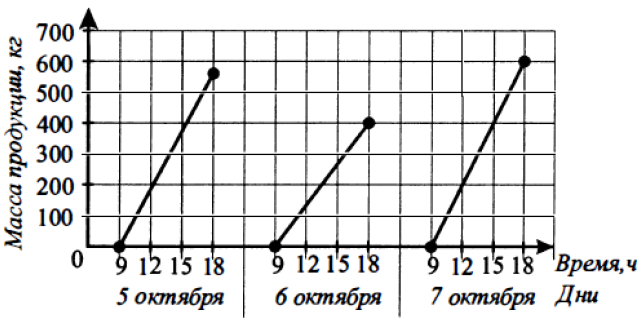
Задание 2
Находим снизу 7 октября 15 часов и поднимаемся вверх. Придём в 400.
Задание 3
Найдём координаты $$M$$: $$x_M=\frac{-7+1}{2}=-3$$; $$y_M=\frac{-2+5}{2}=1,5$$.
Получим: $$M(-3;1,5)$$.
Тогда $$|CM|=\sqrt{(-3-3)^2+(1,5-4)^2}=\sqrt{36+6,25}=\sqrt{42,25}=6,5$$.
Задание 4
$$A=0,2$$ – перегорит 1 лампа
$$B=0,2$$ – перегорит 2 лампа
$$\overline{A}=\overline{B}=1-0,2=0,8$$
$$P(\overline{AB})=0,8\cdot0,8=0,64$$ – не перегорят обе лампы
Тогда противоположная вероятность данной и будет искомой вероятностью
$$P_{иск}=1-0,64=0,36$$
Задание 5
Если уравнение имеет несколько корней, то в ответе укажите наибольший корень.
Умножим все уравнение на $$(\sqrt[3]{3+\sqrt{8}})^x$$
И сделаем замену $$t=(\sqrt[3]{3+\sqrt{8}})^x$$
$$t:2−6t+1=0$$
$$t=3\pm\sqrt{8}$$
Делаем обратную замену
$$(3+\sqrt{8})^{x/3}=(3+\sqrt{8})^1$$
$$(3+\sqrt{8})^{x/3}=(3-\sqrt{8})^1$$ – тут аналогично умножаем на $$(3+\sqrt{8})^{x/3}$$
$$x=3$$
$$(3+\sqrt{8})^{\frac{3+x}{3}}=1$$, откуда $$x=−3$$
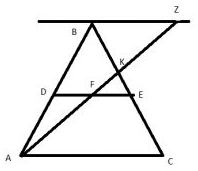
Задание 6
Сделаем доп. построение. Построим прямую || AC из точки B, продолжим прямую AK до пересечения с этой прямой. Пусть они пересекаются в точке Z.
AK-легче всего найти из треугольника ABK по т косинусов (угол B=60, т.к равносторонний треугольник). Но нам нужно знать BK
$$\Delta BKZ$$ подобен $$\Delta EKF$$ – по 2-м углам
$$BZ=2DF$$ (DF-средняя линия треугольника ABZ)
значит $$\frac{BK}{KE}=\frac{BZ}{FE}=2$$
$$BK=2KE$$
$$BE=BK+KE=3KE$$, откуда $$KE=\frac{1}{3}BE$$ и $$BK=\frac{2}{3}BE$$ $$(BE=0,5BC=0,5AC)$$
Мы всё знаем, применяем теорему косинусов
$$AK^2=AB^2+BK^2-2AB\cdot BK\cdot\cos60)$$
Подставляя все известные нам данные получаем ответ
Задание 8
Тут все очень легко
Пусть $$a,b,c$$ – измерения (стороны) нашего прямоугольного параллелепипеда
Тогда из условия
$$ab=4$$
$$ac=8$$
$$bc=32$$
$$a=\frac{8}{c}$$
$$a\cdot\frac{32}{c}=4$$
$$c^2=32\cdot2$$
и исходя из этого
$$a=\frac{8}{\sqrt{c}}$$
$$b=\frac{32}{\sqrt{c}}$$
$$d=\sqrt{a^2+b^2+c^2}=\sqrt{81}=9$$
Задание 9
$$\frac{\sin^2\frac{\pi}{5}\cdot\cos^2\frac{\pi}{5}}{1-\cos^4\frac{2\pi}{5}-\cos^2\frac{2\pi}{5}\cdot\sin^2\frac{2\pi}{5}}$$
$$\frac{\sin^2\frac{\pi}{5}\cdot\cos^2\frac{\pi}{5}}{1-\cos^4\frac{2\pi}{5}-\cos^2\frac{2\pi}{5}\cdot\sin^2\frac{2\pi}{5}}=\frac{\sin^2\frac{\pi}{5}\cdot\cos^2\frac{\pi}{5}}{1-\cos^2\frac{2\pi}{5}(\cos^2\frac{2\pi}{5}+\sin^2\frac{2\pi}{5}}=\frac{0,25\sin^2\frac{2\pi}{5}}{\sin^2\frac{2\pi}{5}}=0,25$$
Задание 10
Задание 11
Пусть за апрель было $$x$$, обозначим за $$y$$ – ежемесячное увеличение
Т.е. в мае будет $$x+y$$, в июне $$x+2y$$ и т.д.
Тогда легко можно составить систему
$$\left\{\begin{matrix} 2x+y=9500\\ x+6y=7500 \end{matrix}\right.$$
Нужно решить данную систему
$$(x,y)=(4500,500)$$
В июнь было $$x+2y=5500$$
Задание 12
$$y=\sin^2\frac{4\pi}{3x^4-4x^3+13}$$
Найдем критические точки:
$$y'=0$$
Так как требуется искать наибольшее значение функции, то можно искать точку максимума у аргумента этого синуса, т.е. мы себе упрощаем вычисления. Но можно еще упростить, максимум будет тогда, когда знаменатель будет минимален, найдем эту точку.
$$12x^3-12x^2=0$$
$$12x^2(x-1)=0$$
$$x=0$$ - здесь нет экстремума
$$x=1$$
По методу интервалов $$x=1$$ – точка максимума
$$y(1)=\sin^2\frac{4π}{12}=0,75$$