312 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.

Цена товара изменилась три раза, первый раз повысилась на 40%, второй раз повысилась на 25%, а в результате трехкратного изменения повысилась всего на 96%. На сколько процентов изменилась цена в третий раз?

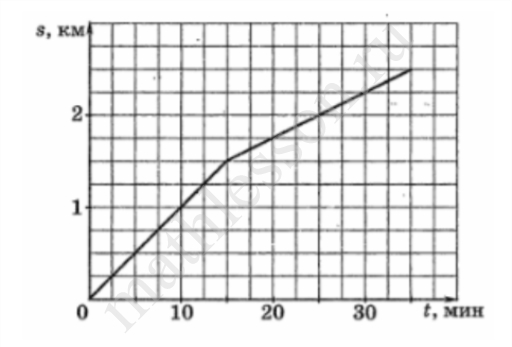
Турист во время прогулки сначала шел по ровной проселочной дороге, а потом дорога пошла в гору. На рисунке изображен график его движения. По вертикальной оси откладывается длина пройденного им пути, а по горизонтальной – время движения. Определите, с какой скоростью турист шел в гору. Ответ выразите в км/ч.

В трапеции ABCD с основаниями AD=22 и ВС=8 см проведена средняя линия KN, которая пересекает диагонали АС и BD в точках L и М соответственно. Найдите длину отрезка LM.

Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найдите вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

Найдите площадь правильного двенадцатиугольника, если его сторона равна $$6\sqrt{2-\sqrt{3}}$$ .

Под каким углом пересекаются касательные к графикам функций $$y=\cos x$$ в точке $$x_{0}=\frac{3\pi}{2}$$ и $$y=\sqrt{3}\cos x$$ в точке $$x_{0}=\frac{\pi}{2}$$ ? Ответ запишите в градусах.

Полная поверхность усеченного конуса равна $$572\pi$$ м², а длины радиусов оснований равны 6 м и 14 м. Определить (в метрах) длину высоты усеченного конуса.

Найдите значение выражения $$\cos 2t-\sqrt{3}\sin (\frac{15\pi}{2}-t)$$, при $$t=\frac{11\pi}{6}$$

Мотоциклист, движущийся по городу со скоростью $$v_{0}=50$$ км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением $$a=12$$ км/ч². Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением $$S=v_{0}t+\frac{at^{2}}{2}$$. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее, чем в 26,5 км от города. Ответ выразите в минутах.

Два станка одновременно начали штамповать детали с производительностью 70 деталей в минуту каждый. Через час пустили в работу третий станок. В этот момент первый станок снизил свою производительность на 10 деталей минуту. Через некоторое время на третьем станке было сделано столько деталей, сколько было к тому моменту на первом, а еще через 3,5 часа он сравнялся по числу сделанных деталей со вторым. Найдите, сколько деталей в минуту штампует третий станок.

Найдите наибольшее значение функции $$y=\frac{\ln(2x-3)}{2}+3x-x^{2}$$

В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ стороны основания равны 2, а боковые ребра равны 4. Точка N – середина отрезка АС.

Решите неравенство: $$\log_{\sqrt[3]{9x}}\sqrt{\frac{x^{3}}{3}}+\log_{\sqrt[3]{3x^{2}}}\sqrt{27x}\leq 3$$

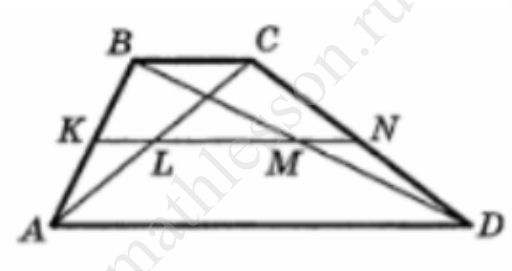
В остроугольном треугольнике АВС проведены биссектриса AD и медиана ВЕ. Точки M и N являются ортогональными проекциями на сторону АВ точек D и Е соответственно, причем $$\frac{AM}{MB}=\frac{9}{1}$$, $$\frac{AN}{NB}=\frac{2}{3}$$ .

Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими начинками: ягодная, творожная и мясная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.

Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц.

Найти все значения параметра a, при которых уравнение $$\frac{(x^{2}-4x+a)^{3}}{2}=(a-4x)(3x^{4}+(a-4x)^{2})$$ имеет единственное решение на промежутке $$(-2-\sqrt{2};0]$$

В ячейках таблицы 5 на 9 расставлены натуральные числа, среди которых ровно 33 нечетных. Александра рассматривает пары соседних ячеек, имеющих общую сторону. Если произведение чисел в паре четно, наша героиня считает такую пару зачетной.