365 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 2
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)$$ – вероятность наступления 2-х несовместных событий
$$A_1$$ – исправная батарейка забракована системой
$$A_2$$ – неисправная батарейка забракована системой
$$P(A_1)=0,97\cdot0,03$$
$$P(A_2)=0,03\cdot0,96$$
$$P(A)=0,97\cdot0,03+0,03\cdot0,96=0,0579$$
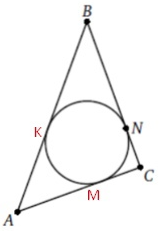
Задание 3
$$P=AB+AC+BC$$
$$P=AK+BK+BN+NC+AC$$
По свойству касательных, проведенных из одной точки
$$AK=AM$$
$$NC=MC$$
$$BK=BN=15$$
$$AC=AM+MC=AK+NC$$
Значит
$$P=17+17+15+15=64$$
Задание 4
$$\frac{3^{2x+22}\cdot2^{3x+8}}{3^{2x+21}\cdot2^{2x+8}}=3\cdot2^x=12$$
Задание 5
Пусть $$a$$ - сторона квадрата
Если диагональ перпендикулярна плоскости основания, то из прямоугольного треугольника мы можем найти диагональ квадрата, который лежит в основании.
$$\sqrt{36-14\cdot7}=2\sqrt{2}=a\sqrt{2}$$
$$a=2$$
$$S=4$$
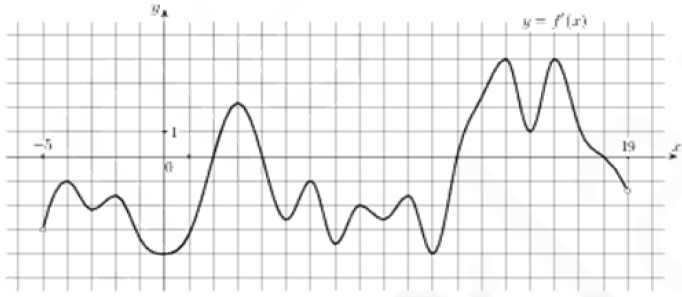
Задание 6
Точка максимума будет там, где знак производной меняется с “+” на “-”
Задание 7
$$3\cdot\sin\frac{\pi t}{4}>1,5$$
$$\sin\frac{\pi t}{4}>\frac{1}{2}$$
$$\frac{\pi}{6}+2\pi n<\frac{\pi t}{4}<\frac{5\pi}{6}+2\pi n$$
$$\frac{2}{3}+8n<t<\frac{10}{3}+8n$$
$$n=0$$
$$\frac{2}{3}<t<3\frac{1}{3}$$
$$\frac{2}{3}<t<1$$
Получаем, что $$1−\frac{2}{3}=\frac{1}{3}\approx0,33$$ доля от первой секунды скорость была больше 1,5
Задание 8
Пусть $$x, y$$ – цена принтера и компьютера соответственно, $$k,n$$ – кол-во проданных принтеров и компьютеров соответственно.
$$x\cdot k=y\cdot n$$
$$\left\{\begin{matrix} x\cdot n=192\\ y\cdot k=75 \end{matrix}\right.$$Решая систему, получаем $$\frac{x}{y}=1,6$$
$$\Rightarrow 60\%$$
Задание 10
Всего благоприятных вариантов из 36 два: 5,6 и 6,5
Найдем вероятность того, что гостю ни разу не выпала комбинация 5,6:
$$P(A)=(1-\frac{2}{36})\cdot(1-\frac{2}{36})$$
$$P_{иск}=1−P(A)=\frac{35}{324}\approx0,11$$
Задание 11
Найдем критические точки:
$$y'=0$$
$$12\cos x−6\sqrt{3}=0$$
$$\cos x=\frac{\sqrt{3}}{2}$$
$$x=\pm\frac{\pi}{6}+2\pi n$$
Под отрезок попадает только $$x=\frac{\pi}{6}$$
Проверкой методом интервалов эта точка и является точкой максимума
$$y(\frac{\pi}{6})=12$$