310 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.

Яблоки подешевели на 20%. Сколько килограмм яблок можно теперь купить на те же деньги, на которые раньше покупали 2,8 кг яблок?

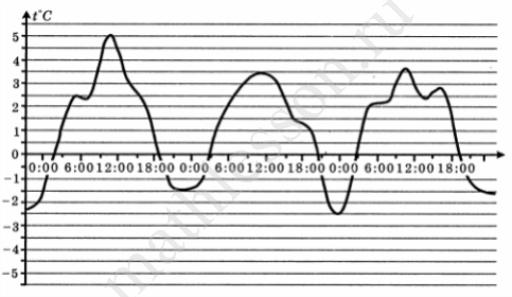
На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов 2 марта. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Найдите по графику наибольшую температуру воздуха 3 марта в градусах Цельсия.

Внутри параллелограмма ABCD, площадь которого равна 10, отмечена точка М. Найдите сумму площадей треугольников AMВ и CMD.

Бросаются одновременно две игральные кости. Найдите вероятность того, что сумма выпавших очков будет больше, чем их произведение. Ответ округлите до сотых.

В равнобедренном треугольнике АВС с основанием АС высоты ВМ и АН пересекаются в точке К, причем АК=5, КН=3. Найдите площадь треугольника АВК.

На рисунке изображен график производной функции $$y=f(x)$$, заданной на отрезке [‒ 2; 6]. Найдите число точек на этом отрезке, в которых касательная к графику функции $$f(x)$$ параллельна биссектрисе первой четверти.

Боковое ребро правильной треугольной призмы на 20% больше ее стороны основания. Расстояние между серединами двух непараллельных ребер, принадлежащих разным основаниям, равно 13. Найдите площадь боковой поверхности призмы.

В ходе распада радиоактивного изотопа его масса уменьшается по закону $$m(t)=m_{0}\cdot 2-\frac{t}{T}$$, где $$m_{0}$$ ‐ начальная масса изотопа, t (мин) – прошедшее от начального момента время, T ‐ период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени m₀=156 мг изотопа, период полураспада которого T=8 мин. В течение скольких минут масса изотопа будет не меньше 39 мг?

Двум операторам поручили набрать на компьютере текст книги объемом 315 страниц. Один оператор, отдав второму 144 страницы книги, взял остальные страницы себе. Первый выполнил свою работу за 19 дней, а второй свою – за 12. На сколько процентов нужно было увеличить часть работы второго оператора (уменьшив часть работы первого), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое число дней?

Найдите наибольшее значение функции $$y=3x-e^{3x}$$ на отрезке $$[-1;1]$$

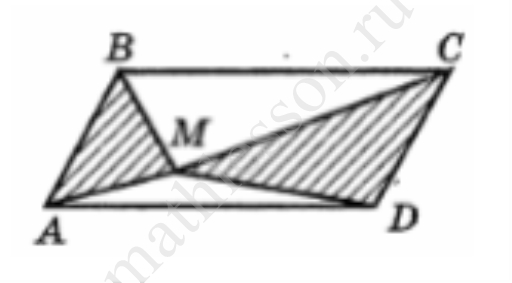
Основание пирамиды SABCD – квадрат ABCD, боковое ребро SA перпендикулярно плоскости основания. BC=2SA. Точка М – середина ребра АВ.

Решите неравенство: $$\log_{x+4}(x^2-8x+12)<\frac{1}{2}\log_{|x-2|}(2-x)^2$$

В треугольнике АВС $$\angle B=70^{\circ}$$, $$\angle C=25^{\circ}$$, BD - диаметр описанной около треугольника АВС окружности. Продолжение высоты ВН пересекает окружность в точке L.

Правительство решило закрыть нерентабельные шахты и построить новые фабрики и заводы. В результате закрытия одной шахты увольняется 180 человек, при этом на консервацию шахты и выплату пособий увольняемым тратится 52 млн. рублей. Строительство одного нового завода с персоналом 170 человек стоит 43 млн. рублей, а одной фабрики с персоналом 110 человек – 20 млн. рублей. Чему равно максимально возможное увеличение суммарного числа новых рабочих мест, если известно, что сумма всех затрат правительства составила ровно 714 млн. рублей?

Найдите все значения параметра a , при каждом из которых функция $$f(x)=x(1-a)+3(1-2a)\sin \frac{x}{3}+\frac{3}{2}\sin \frac{2x}{3}+\pi a$$ имеет не более двух экстремумов на промежутке $$(\pi;5\pi)$$

За круглым столом сидели 110 человек, а на столе лежали абрикосы. Для каждой пары соседей число съеденных ими абрикосов отличается на 3.