391 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$\log_{x+1}(x^2-7x+1)=1$$
$$(*):$$ $$\left\{\begin{matrix} x+1>0\\ x+1\neq1\\ x^2-7x+1>0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x>-1\\ x\neq0\\ x^2-7x+1>0 \end{matrix}\right.$$
$$x+1=x^2-7x+1$$
$$x^2-8x=0$$
$$x(x-8)=0$$
$$x=0 \notin (*)$$
$$x=8$$
Задание 2
$$P(A)=\frac{43}{50}\cdot\frac{42}{49}\cdot\frac{7}{48}\approx0,1075$$
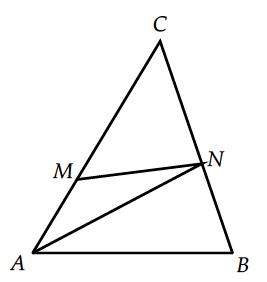
Задание 3
$$S_{ANM}=\frac{1}{2}\cdot AM\cdot h_{AMN}=11$$
$$AM\cdot h_{AMN}=22$$
$$\frac{AM}{MC}=\frac{2}{3}=\frac{2x}{3x}\Rightarrow AC=AM+MC=2x+3x=5x\Rightarrow$$
$$\frac{AC}{AM}=\frac{5x}{2x}=\frac{5}{2}\Rightarrow AC=AM\cdot\frac{5}{2}$$
$$\frac{BN}{NC}=\frac{4y}{5y}\Rightarrow BC=BN+NC=4y+5y=9y$$
Отношение высот $$h_{ABC}$$ и $$h_{AMN}$$ равно отношению $$\frac{BC}{NC}\Rightarrow$$
$$\frac{h_{ABC}}{h_{AMN}}=\frac{9y}{5y}=\frac{9}{5}\Rightarrow h_{ABC}=h_{AMN}\cdot\frac{9}{5}$$
$$S_{ABC}=\frac{1}{2}\cdot AC\cdot h_{ABC}=\frac{1}{2}\cdot (AM\cdot\frac{5}{2})\cdot (h_{AMN}\cdot\frac{9}{5})=$$
$$=\frac{1}{2}\cdot AM\cdot h_{AMN}\cdot\frac{45}{10}=S_{ANM}\cdot\frac{45}{10}=11\cdot\frac{45}{10}=49,5$$
Задание 4
$$\frac{\log_2 800}{\log_{800}2}-\frac{\log_2 625}{\log_{160}2}=\log_2^2(2^5\cdot25)-\log_2 25^2-\log_2(2^5\cdot5)$$
$$=(5+2\log_2 5)^2-4\log_2 5(5+\log_2 5)=$$
$$=25+20\log_2 5+4\log_2^2 5-20\log_2 5-4\log_2^2 5=25$$
Задание 5
$$S_1=6а^2$$
$$S_2=6(a-3)^2$$
$$6a^2-6(a-3)^2=126$$
$$6a^2-6a^2+36a-54=126$$
$$36a=180$$
$$a=5$$
Задание 6
$$\left\{\begin{matrix} (80x+76)'=(x^3-3x^2+8x-100)'\\ 80x+76=x^3-3x^2+8x-100 \end{matrix}\right.$$
Рассмотрим первое уравнение:
$$80=3x^2-6x+8\Leftrightarrow 3x^2-6x-72=0\Rightarrow x^2-2x-24=0\Rightarrow\left[\begin{matrix} x=6\\ x=-4 \end{matrix}\right.$$
Проверим $$x=6: 6\cdot80+36\neq6^3-3\cdot6^2+6\cdot8-100$$
При $$x=-4: y=80\cdot(-4)+76=-244$$
Задание 7
Чем больше ускорение, тем больше конечная скорость. Значит, максимальную скорость авто разовьёт при максимальном ускорении.
$$V^2=2Sa=2\cdot1,5\cdot7500=22500$$
$$V=\sqrt{22500}=\pm150$$
Отрицательный корень отбрасываем, т.к. скорость не может быть отрицательной.
Задание 8
Для удобства сразу переведём проценты в десятичные дроби:
100% - 1
60% - 0,6
70% - 0,7
40% - 0,4
$$1+0,6=1,6$$ (или 160%) - составила продажная цена товара от закупочной цены
$$1-0,4=0,6$$ (или 60%) - составила цена товара после уценки на 40%
$$1,6\cdot0,6=0,96$$ (или 96%) - составила цена товара после уценки по отношению к первоначальной продажной цене
$$1-0.7=0,3$$ (или 30%)- от товара продано с уценкой на 40%
$$0,7\cdot1,6+0,3\cdot0,96=1,408$$ (или 140,8%) - составила общая продажная цена на товар
$$1,408-1=0,408$$ (или 40,8%) - составила прибыль магазина от закупочной цены
Задание 9
Точки $$(2;1)$$ и $$(-4;-1)$$ принадлежат графику функции. Тогда:
$$\left\{\begin{matrix} \frac{k}{2+a}=1\\ \frac{k}{-4+a}=-1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} k=2+a\\ k=4-a \end{matrix}\right.$$
$$2+a=4-a$$
$$2a=2$$
$$a=1$$
$$k=4-1=3$$
$$f(x)=\frac{3}{x+1}$$
$$f(19)=\frac{3}{19+1}=\frac{3}{20}=0,15$$
Задание 10
Вероятность поразить первым выстрелом $$0,3,$$ вторым $$0,7\cdot0,3=0,21.$$ Значит, за 2 выстрела $$0,3+0,21=0,51.$$ Не поразить за 2: $$0,7\cdot0,7=0,49.$$
Тогда ровно 3 мишени: $$0,51\cdot0,51\cdot0,51\cdot0,49\cdot0,49\cdot0,49;$$ ровно 4 мишени: $$0,51^4\cdot0,49^2$$
Получим: $$\frac{(0,51)^3\cdot(0,49)^3\cdot C^3_6}{0,51^4\cdot0,49^2\cdot C^4_6}=\frac{0,49\cdot C^3_6}{0,51\cdot C^4_6}$$
$$C^3_6$$ - количество комбинаций трёх попаданий
$$C^4_6$$ - количество комбинаций четырёх попаданий
$$C^3_6=\frac{6!}{3!(6-3)!}=\frac{6!}{3!\cdot3!}=\frac{3!\cdot4\cdot5\cdot6}{3!\cdot1\cdot2\cdot3}=20$$
$$C^4_6=\frac{6!}{4!(6-4)!}=\frac{4!\cdot5\cdot6}{4!\cdot1\cdot2}=15$$
$$P(A)=\frac{49}{51}\cdot\frac{20}{15}\approx1,28$$
Задание 11
$$(x^3-\frac{48}{x^2})'=\frac{3(x^5+32)}{x^3}$$
$$\frac{3(x^5+32)}{x^3}=0$$
$$x^5+32 = 0$$
$$x^5= -32 $$
$$x= - 2$$ входит в отрезок $$[-3;2]$$
$$y(-2)=(-2)^3-\frac{48}{(-2)^2}=-20$$
$$y(-3)=(-2)^3-\frac{48}{(-2)^2}=-\frac{97}{3}=-32 1/3$$
$$y(2)=2^3-\frac{48}{2^2}=-4$$
Наибольшее значение функции в точке $$x=2 ; y= -4$$
Ответ: $$- 4$$