236 вариант Алекса Ларина. Разбор ЕГЭ математика 2018.
Решаем ЕГЭ 236 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №236 (alexlarin.com)
Решаем ЕГЭ 236 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №236 (alexlarin.com)
Задание 1
Одна таблетка лекарства весит 40 мг и содержит 6% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописывает 1,2 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в возрасте четырёх месяцев и весом 6 кг в течение суток?
В одной таблетке активного вещества: $$40*0,06=2,4$$мг Ребенку на 6 кг массы активного вещества: $$6*1,2=7,2$$мг Количество таблеток: $$n=\frac{7,2}{2,4}=3$$
Задание 2
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой.
Положительная среднемесячная температура была с 4 по 10 месяц включительно, то есть 7 месяцев
Задание 3
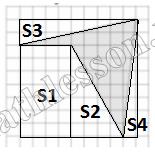
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Задание 4
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 6 очков в двух играх. Если команда выигрывает, она получает 4 очка, в случае ничьей – 2 очка, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Вероятность ничьи: $$1-0,3-0,3=0,4$$ Проходит в случае двух побед или же одной победы и ничьи: 2 победы:$$0,3*0,3=0,09$$ Победа и ничья: может быть два варианта - сначала победа, потом ничья и наоборот: $$0,3*0,4+0,4*0,3=0,24$$ Тогда итоговая вероятность:$$P=0,09+0,24=0,33$$
Задание 5
Найдите корень уравнения $$\sqrt[3]{2x+5}=-3$$
$$\sqrt[3]{2x+5}=-3$$. Возведем обе части в куб $$2x+5=-27 \Leftrightarrow$$$$2x=-27-5|:2 \Leftrightarrow$$$$x=-16$$
Задание 6
Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 36. Найдите его площадь.
Воспользуемся формулой площади фигуры через ее полупериметр и радиус вписанной окружности: $$S=pr \Leftrightarrow$$$$S=\frac{36}{2}*2=36$$
Задание 7
На рисунке изображен график $$y=f'(x)$$ – производной функции у = f (x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции у = f (x), принадлежащих отрезку [−14; 2].
Экстремумы функции расположены там, где производная функции равна 0, то есть там, где график производной пересекает ось Ох. На заданном отрезке таких точек 4 (с абсциссами: -13 ; -11 ; -9 ; -7)
Задание 8
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Объем пирамиды находится как треть произведения площади основания, на проведенную к нему высоту. Примем за основание грань $$ABS$$, тогда высота к ней будет $$SC$$. В таком случае объем: $$V=\frac{1}{3}*\frac{1}{2}*3*3*3=4,5$$
Задание 9
Найдите значение выражения $$\sin\frac{7\pi}{6}\cdot\cos\frac{5\pi}{3}$$
$$\sin\frac{7\pi}{6}\cdot\cos\frac{5\pi}{3}=$$$$\sin(\pi+\frac{\pi}{6})\cdot\cos(2\pi-\frac{\pi}{3})=$$$$-\sin\frac{\pi}{6}\cdot\cos\frac{\pi}{3}=$$$$-\frac{1}{2}*\frac{1}{2}=-0,25$$
Задание 10
Перед отправкой тепловоз издал гудок с частотой $$f_{0}=490$$ Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из‐за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону $$f(v)=\frac{f_{0}}{1-\frac{v}{c}}$$, где с-скорость звука в воздухе (в м\с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловозесли человек смог различить сигналы. Считать, что с = 340 м\с. Ответ выразите в м/с.
Частота второго должна быть выше минимум на 10 Гц, тогда: $$500=\frac{490}{1-\frac{v}{340}}$$. Перемножим "крест-накрест" $$500-\frac{500v}{340}=490$$ $$\frac{500v}{340}=10$$ $$v=\frac{340*10}{500}=6,8$$
Задание 11
Имеется два сосуда. Первый содержит 100 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 67% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 77% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Пусть х - концентрация первого, y - концентрация второго, тогда в первом кислоты $$100x$$ кг, во втором - $$20y$$ кг. Получили третий раствор массой 120 кг, в котором $$120*0,67$$ кг кислоты. Во втором случае смешаем равные (по 20 кг) массы растворов, тогда: $$\left\{\begin{matrix}100x+20y=0,67*120\\20x+20y=0,77*40 \end{matrix}\right.$$ Вычтем из первого уравнения второе: $$80x=80,4-30,8=49,6|:80$$ $$x=0,62$$ Тогда масса кислоты в первом: $$0,62*100=62$$ кг
Задание 12
Найдите наименьшее значение функции $$y=(x^{2}-4x+4)\cdot e^{2}$$ на отрезке $$[-1;3]$$
Найдем производную данной функции и приравняем ее к нулю: $$y'=(2x-4)e^{x}+e^{x}*(x^{2}-4x+4)=0$$ $$e^{x}(2x-4+x^{2}-4x+4)=0$$ Число $$e^{x}$$ всегда положительно, поэтому можем его убрать: $$x^{2}-2x=0$$ Тогда $$x=0 ; x=2$$ Начертим координатную прямую, расставим знаки производной и получим, что $$x=2$$ - точка минимума, то есть в ней будет наименьшее значение функции на заданном в условии отрезке: $$y(2)=(2^{2}-4*2+4)e^{2}=0$$
Задание 13
Дано уравнение $$\frac{1}{\cos2x\cdot\cos x}=\frac{1}{\sin2x\cdot\sin x}$$
A) $$\frac{1}{\cos 2x *\cos x}=\frac{1}{\sin 2x*\sin x}$$
Найдем область определения:
$$\left\{\begin{matrix}\cos 2x\neq 0 \\\cos x \neq 0 \\\sin 2x \neq 0 \\\sin x \neq 0 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x \neq \frac{\pi}{4}+\frac{\pi n}{2} \\x \neq \frac{\pi}{2}+\pi n \\x \neq \frac{\pi n }{2} \\x \neq \pi n \end{matrix}\right.\Leftrightarrow$$ $$x \neq \frac{\pi n}{4}, n \in Z$$
$$\cos 2x*\cos x=\sin 2x*\sin x\Leftrightarrow$$$$(\cos^{2}x-\sin^{2}x)\cos x-2 \sin x\cos x\sin x=0\Leftrightarrow$$$$\cos^{3}x-\sin^{2}x\cos x-2 \sin^{2}x \cos x=0\Leftrightarrow$$$$\cos^{3}x-3\sin^{2}x \cos x=0\Leftrightarrow$$$$\cos x(\cos^{2}x-3 \sin ^{2}x)=0$$
$$\left\{\begin{matrix}\cos x=0 \\1-\sin^{2}x-3 \sin^{2}x=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{2}+\pi n , n \in Z \notin (1) \\\sin ^{2}x=\frac{1}{4} \end{matrix}\right.\Leftrightarrow$$$$\sin x=\pm \frac{1}{2}\Leftrightarrow$$$$\left\{\begin{matrix}x=(-1)^{n}\frac{\pi}{6}+\pi n, n \in Z \\x=(-1)^{n+1}\frac{\pi}{6}+\pi n, n \in Z \end{matrix}\right.$$
Б) Начертим единичную окружность, отметим заданный промежуток и полученные корни.
Видим, что в заданный промежуток попали:
$$\frac{\pi}{6}+2\pi n$$:$$-2\pi+\frac{\pi}{6}=-\frac{11\pi}{6}$$
$$\frac{5\pi}{6}+2\pi n$$:$$-\pi-\frac{\pi}{6}=-\frac{7\pi}{6}$$
$$-\frac{5\pi}{6}+2\pi n$$:$$-\pi+\frac{\pi}{6}=-\frac{5\pi}{6}$$
Задание 14
Дан куб $$ABCDA_{1}B_{1}C_{1}D_{1}$$. Пусть $$l$$ – линия пересечения плоскостей $$ACD_{1}$$ и $$BDC_{1}$$
A) введем систему координат. Пусть ребро куба 2. Тогда :$$H(1;1;0), M(1;0;1), D(0;0;0), B_{1}(2;2;2)$$
$$\vec{HM} (0;-1;1)$$; $$\vec{DB_{1}} (2;2;2)$$
$$\cos (HM; BD)=\frac{10*2+(-1)*2+1*2}{\sqrt{2}*\sqrt{12}}=0\Rightarrow$$ угол равен 90
Б) Построим из H прямую $$HK\left | \right | DB_{1}$$$$\Rightarrow \Delta DB_{1}B\sim \Delta HKB$$; H-середина DB, то и K-середина
$$BB_{1}\Rightarrow K(2;2;1)$$
Зададим уравнение (HKM):
$$\left\{\begin{matrix}a+b+d-0\\a+c+d=0 \\2a+ab+c+d=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}b=c \\a+c+d=0 \\2a+3c+d=0\end{matrix}\right.$$$$\left\{\begin{matrix}a=-c-d \\-2c-2d+3c+d=0 \\b=c \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}c=d \\b=c \\a=-2c\end{matrix}\right.$$
Получим: $$-2cx+cy+cz+c=0|:c \Leftrightarrow$$$$-2x+y+z+1=0$$
Найдем расстояние от D до (HKM)
$$r=\frac{\left | -2*0+1*0+1*0+1 \right |}{\sqrt{4+1+1}}=\frac{1}{\sqrt{6}}$$
Задание 15
Решите неравенство $$\log_{x^{2}}(3-x)\leq\log_{x+2}(3-x)$$
$$\log _{x^{2}}(3-x)\leq \log_{x+2}(3-x)$$
Найдем область определения функции:
$$\left\{\begin{matrix}x^{2}>0 \\x^{2}\neq1 \\3-x>0\\x+2>0\\x+2 \neq1 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x\neq 0 \\x \neq \pm 1 \\x<3 \\x>-2 \end{matrix}\right.\Leftrightarrow$$$$x \in (-2-;1)\cup (-1;0)\cup (0;1)\cup (1;3)$$
$$\frac{1}{\log _{3-x}x^{2}}-\frac{1}{\log_{3-x}(x+2)}\leq 0\Leftrightarrow$$$$\frac{\log_{3-x}(x+2)-\log_{3-x}x^{2}}{\log_{3-x}x^{2}*\log_{3-x}(x+2)}\leq 0\Leftrightarrow$$$$\frac{\log_{3-x}\frac{x+2}{x^{2}}}{\log_{3-x}x^{2}*\log_{3-x}(x+2)}\leq 0\Leftrightarrow$$$$\frac{\log_{x^{2}} \frac{x+2}{x^{2}}}{\log_{3-x}(x+2)}\leq 0$$
Воспользуемся методом рационализации:
$$(\frac{x+2}{x^{2}}-1)(x^{2}-1)(3-x-1)(x+2-1)\leq 0\Leftrightarrow$$$$\frac{x+2-x^{2}-1}{x^{2}}*(x-1)(x+1)(2-x)(x+1)\leq 0\Leftrightarrow$$$$\frac{-(x+1)(x-2)}{x^{2}}*(x-1)(x+1)^{2}(2-x)\leq 0\Leftrightarrow$$$$\frac{(x+1)^{3}(x-2)^{2}(x-1)}{x^{2}}\leq 0$$
С учетом области определения: $$x \in (-1;0)\cup (0;1)\cup 2$$
Задание 16
В тупоугольном треугольнике АВС ($$\angle C$$ - тупой) на высоте ВН как на диаметре построена окружность, пересекающая стороны АВ и СВ в точках Р и К соответственно.
А) Докажите, что $$\sin\angle ABC=\frac{PH}{BC}-\frac{KH}{BA}$$
Б) Найдите длину отрезка РК, если известно, что $$BA=13$$, $$BC=8$$, $$\sin\angle ABC=\frac{7\sqrt{3}}{26}$$
A) 1) $$\sin \angle ABC =\frac{PH}{BC}-\frac{KH}{BA}=$$$$\frac{PH*BA-KH*BC}{BC*BA}$$
2) $$PH\perp AB$$(т.к. опирается на диаметр); $$KH\perp BC$$(т.к. опирается на диаметр)
3) $$\sin \angle ABC=\frac{2S_{AHB}-S_{BCH}}{BC*BA}=$$$$\frac{2S_{ABC}}{BC*BA}=$$$$\frac{2*\frac{1}{2}BC*BA*\sin\angle ABC}{BC*BA}=\sin\angle ABC$$
Б) 1) $$\Delta ABC*\cos ABC=\sqrt{1-\sin^{2}ABC}=\sqrt{1-\frac{147}{676}}=\frac{23}{26}$$
$$AC=\sqrt{AB^{2}+BC^{2}-2 AB*BC\cos ABC}=\sqrt{13^{2}+8^{2}-2*13*8*\frac{23}{26}}=7$$
2) $$S_{ABC}=\frac{1}{2}AC*BH=\frac{1}{2}AB*BC*\sin ABC$$; $$BH=\frac{13*8*\frac{7\sqrt{3}}{26}}{7}=4\sqrt{3}$$
3) $$\cos CBH=\frac{BH}{CB}=\frac{4\sqrt{3}}8{}=\frac{\sqrt{3}}{2}$$, тогда $$\angle CBH=30$$ и $$KB=BH*\cos CBH=4\sqrt{3}*\frac{\sqrt{3}}2{}=6$$
4) $$\angle HCB=90-\angle CBH=60\Rightarrow \angle ACB=120$$; $$\angle KHB=90-\angle CBH=60\Rightarrow \angle KPB=120$$(т.к. HKPB-вписанный). Тогда $$\Delta KPB\sim \Delta ABC\Rightarrow \frac{KB}{AB}=\frac{KP}{AC}\Rightarrow KP=\frac{6*7}{13}=\frac{42}{13}$$
Задание 17
Иван Иванович попросил у своего соседа Ивана Никифоровича взаймы на несколько дней 648 тысяч рублей, пообещав вернуть долг с процентами. Иван Никифорович заявил, что если он даст в долг на п дней S рублей, то сосед должен будет вернуть сумму, равную $$S(1+\frac{n}{300})+\frac{S}{n^{2}}$$. После недолгих раздумий Иван Иванович согласился на предложенные условия. Через сколько дней Ивану Ивановичу следует рассчитаться с долгом, чтобы выплаты оказались наименьшими? Сколько в этом случае составит переплата сверх взятой в долг суммы?
$$S(1+\frac{n}{300})+\frac{S}n^{2}=S(1+\frac{n}{300}+\frac{1}{n^{2}})$$
Пусть $$f(n)=1+\frac{n}{300}+\frac{1}{n^{2}}$$, найдем производную данной функции:
$${f}'(n)=\frac{1}{300}+\frac{-2}{n^{3}}=\frac{}{300}-\frac{2}{n^{3}}=0\Leftrightarrow$$$$\frac{n^{3}-600}{n^{3}}=0\Leftrightarrow$$$$n=\sqrt[3]{600}$$
Так как $$8<\sqrt[3]{600}<9$$, и при этом n - число целое, то рассмотрим значение функции в границах:
$$f(8)=1+\frac{8}{300}+\frac{1}{64}=\frac{65}{64}+\frac{2}{75}=$$$$\frac{4875+128}{4800}=\frac{5003}{4800}=1,0422$$
$$f(9)=1+\frac{9}{300}+\frac{1}{81}=\frac{82}{81}+\frac{3}{100}=$$$$\frac{8200+24}{8100}=\frac{8443}{4800}=1,0423$$
Как видим, наименьшее значение будет при n=8:
$$648(\frac{8}{300}+\frac{1}{64})=648(\frac{2}{75}+\frac{1}{64})=$$$$\frac{648(128+75)}{75*64}=\frac{648*203}{75*64}=27,405$$
Отвеь:8; 27,405.
Задание 18
Найдите все значения а, при каждом из которых система $$\left\{\begin{matrix}x^{2}+y^{2}-2ax+2ay\leq0\\x^{2}+y^{2}+6ax+8ay\leq1-10a\end{matrix}\right.$$ имеет ровно одно решение.
$$\left\{\begin{matrix}x^{2}+y^{2}-2ax+2ay\leq 0 \\x^{2}+y2 +6ax+8ay\leq 1-10a \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}-2ax+a^{2}+y^{2}+2ay+a^{2}-2a^{2}\leq 0 \\x^{2}+6ax+9a^{2}+y^{2}+8ay+16a^{2}-25a^{}\leq 1-10a \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}(x-a)^{2}+(y+a)^{2}\leq 2a^{2}(f(x)) \\(x+3a)^{2}+(y+4a)^{2}\leq 25a^{2}-10a+1(g(x)) \end{matrix}\right.$$
f(x)-окружность с центром (a;-a) и $$r=\sqrt{2}|a|$$
g(x)-окружность с центром (-3a;-4a) и $$r=|5a-1|$$??
Чтобы было одно решение, расстояние между центральным равно сумме радиусов(т.к. окружности касается)
$$\sqrt{(-3a-a)^{2}+(-4a-(-a))^{2}}=\left | 5a-1 \right |+\sqrt{2}\left | a \right |$$
$$\sqrt{25a^{2}}=\left | 5a-1 \right |+\sqrt{2}\left | a \right |$$
$$5|a|-\sqrt{2}|a|=|5a-1|$$
1) $$\left\{\begin{matrix}a\leq 0 \\-5a+\sqrt{2}a=-5a+1 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a\leq 0 \\a=\frac{1}{\sqrt{2}} \end{matrix}\right.\Leftrightarrow$$ $$\varnothing$$
2)$$\left\{\begin{matrix}a \in (0;0,2] \\5a-\sqrt{2}a=-5a+1 \end{matrix}\right.\Leftrightarrow$$ $$10a-\sqrt{2}a=1\Leftrightarrow$$$$a=\frac{1}{10-\sqrt{2}}$$
3) $$\left\{\begin{matrix}a>0,2 \\5a-\sqrt{2}a=5a-1 \end{matrix}\right.\Leftrightarrow$$ $$\sqrt{2}a=1\Leftrightarrow$$ $$a=\frac{\sqrt{2}}{2}$$
Объединим полученные значения: $$\frac{1}{10-\sqrt{2}} ;\frac{\sqrt{2}}{2}$$
Задание 19
Из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 составлена обыкновенная дробь А, числитель и знаменатель которой – пятизначные числа (каждая цифра использовалась ровно один раз).
А) Чем больше числитель, тем больше А, тогда надо использовать в числителе большие цифры $$\Rightarrow$$ 98765. В знаменателе наоборот $$\Rightarrow$$ 10234. Следовательно, $$A=\frac{98765}{10234}$$
Б) Да, $$\frac{98760}{12345}$$
В) Чтобы было наименьшим надо, чтобы разница между числителем и знаменателем была наименьшей:
$$\frac{49876}{50123}\Rightarrow \left | A-1 \right |=\frac{247}{50123}\approx 0,0049$$
$$\frac{59874}{60123}\Rightarrow\frac{249}{60123} \approx0,0041$$
$$\frac{69854}{70123}\Rightarrow\frac{269}{70123} \approx0,0038$$
$$\frac{79654}{80123}\Rightarrow\frac{469}{80123}\approx0,0041$$
Как видим, дальше будет увеличение, и, следовательно, наименьшее значение будет $$\frac{69854}{70123}$$