ЕГЭ математика 2017. Разбор варианта Алекса Ларина № 196
Подробный разбор 1,2,3,4,5,6,7,8,9,10,11,12 задания тренировочного варианта ЕГЭ № 196 Ларина
Подробный разбор 13,14,15,16,17,18,19 задания тренировочного варианта ЕГЭ № 196 Ларина
Задание 1
Диагональ экрана телевизора “Sony KD‐65” равна 165 сантиметров. Выразите диагональ экрана этого телевизора в дюймах, если известно, что в одном дюйме 2,54 см. Результат округлите до целого числа дюймов.
165/2.54 ≈ 64.96 ≈ 65
Задание 2
На графике точками отмечена цена (в рублях) одного литра подсолнечного масла «Злато» в одном из супермаркетов Липецка течение первых 12 дней июля. Для наглядности точки соединены отрезками. Определите размах цен (в рублях) на подсолнечное масло «Злато» за указанный период.
Максимальная цена - 80 рублей (3 числа), а минимальная - 60 рублей (12 числа). Получаем размах цен: 80-60 = 20 рублей
Задание 3
Клетка имеет размер 1 см * 1 см. Найдите площадь (в квадратных сантиметрах) закрашенной фигуры, изображенной на рисунке.
Достроим треугольники и введем обозначения как показано на рисунке.
SABC = 0.5 * AC * BO = 0.5 * 8 * 2 = 8
SRHZ= 0.5 * 6 * 1 = 3
SALC = 0.5 * 8 * 4 = 16
SRMZ = 0.5 * 6 * 3 = 9
Sзакрашенной = 8 + 16 - 3 - 9 = 12
Задание 4
В финале чемпионата мира по художественной гимнастике должны выступить 9 спортсменок: три россиянки, по две гимнастки из Болгарии, Греции и Испании. Перед началом выступления спортсменок жеребьевкой распределяют на три группы А, Б и В по три человека в каждой. Найдите вероятность того, что обе испанки окажутся в одной группе.
Рассмотрим случай, что обе испанки попадут в первую группу. Вероятность того, что одна испанка попадет в первую группу :
всего у нас 9 жребиев: 111 222 333 (по три в каждую группу)
Значит, вероятность того, что первая испанка попадет в первую группу = 3 / 9 (три жребия из девяти). Но, тогда осталось в первую группу 2 жребия, а всего жребиев 8. Значит, вероятность того, что вторая попадет в первую группу = 2 / 8 = 1 / 4.
Вероятность того, что обе попадут в первую получается путем перемножения вероятности попадания каждой: $$\frac{1}{3}*\frac{1}{4}=\frac{1}{12}$$. Но это вероятность, что попадут в первую, а таких групп всего три. Значит полученную вероятность умножим на 3: $$\frac{1}{12}*3=0.25$$
Задание 5
Найдите корень уравнения $$ \arccos x= \frac{2\pi }{3}$$
Для того, чтобы решить данное уравнение $$ \arccos x= \frac{2\pi }{3}$$, нам, фактически, надо указать абсциссу, которой соответствует точка $$\frac{2\pi }{3}$$ на единичной окружности. У этой точки координаты $$(-\frac{1}{2};\frac{\sqrt{3}}{2})$$ $$ x = - \frac{1}{2} $$
Задание 6
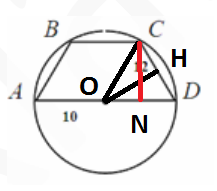
Трапеция АВСD вписана в окружность с диаметром АD. Найдите высоту трапеции, если радиус окружности равен 10, а боковая сторона трапеции равна 12.
Достроим треугольник OCD: OC = OD = 10 - радиусы, OH, CN - высоты. HD = 6 (OH - высота, биссектриса и медиана), отсюда по теореме Пифагора OH = $$\sqrt{OD^{2}-HD^{2}}=8$$.Тогда, используя формулу площади треугольника, получаем:
$$\frac{1}{2} OH*CD = \frac{1}{2} CN*OD$$
$$CN=\frac{OH*CD}{OD}=\frac{8*12}{10}=9.6$$
Задание 7
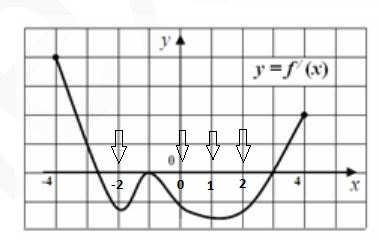
Функция у = f (x) определена на отрезке [‐4; 4]. На рисунке приведен график её производной. Найдите промежутки убывания функции. В ответе укажите сумму всех целых x, входящих в эти промежутки.
Функция убывает, когда производная отрицательная. То есть мы смотрим, где график производной лежит под осью оХ, и выбираем оттуда целые значения Х (в задании надо сумму целых чисел). Важно выбрать значения, где производная равна 0, так как считается, что если функция определена в точках максимума или минимума, то эти точки входят в промежутки возрастания и убывания. Получаем точки -2; -1; 0 ; 1 ; 2 ;3
-2-1+0+1+2+3=3
Задание 8
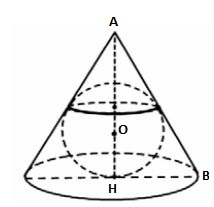
В равносторонний конус (диаметр основания конуса равен длине его образующей) вписан шар. Найдите отношение объема конуса к объему шара.
Объем конуса вычисляется по формуле:
$$V_{1}=\frac{1}{3}S*h=\frac{1}{3}\pi HB^{2}*AH$$
Объем шара вычисляется по формуле:
$$V_{2}=\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi OH^{3}$$
Дан равносторонний конус, то есть в осевом сечении будет равносторонний треугольник. Пусть AB = x, тогда HB = 0,5x и по теореме Пифагора из треугольника AHB: $$AH = \frac{\sqrt{3}}{2}x$$. OH - радиус вписанной в правильный треугольник окружности, и он равен 1/3 от высоты: $$OH = \frac{1}{3}AH = \frac{\sqrt{3}}{6}x$$
Значит объем конуса равен:
$$V_{1}=\frac{1}{3}S*h=\frac{1}{3}\pi (0.5x)^{2}* \frac{\sqrt{3}}{2}x$$
Объем шара равен:
$$V_{2}=\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi (\frac{\sqrt{3}}{6}x)^{3}$$
Тогда:
$$\frac{V_{1}}{V_{2}}=\frac{\frac{1}{3}\pi (0.5x)^{2}* \frac{\sqrt{3}}{2}x}{\frac{4}{3}\pi (\frac{\sqrt{3}}{6}x)^{3}}$$
$$\frac{V_{1}}{V_{2}}=\frac{0.25x^{3}* \frac{\sqrt{3}}{2}}{ 4(\frac{\sqrt{3}}{6}x)^{3}}=2.25$$
Задание 9
Найдите значение выражения $$(\frac{9^{\frac{1}{6}}*9^{\frac{1}{9}}}{\sqrt[18]{9}})^{9}$$
$$(\frac{9^{\frac{1}{6}}*9^{\frac{1}{9}}}{\sqrt[18]{9}})^{9}=(\frac{9^{\frac{1}{6}+\frac{1}{9}}}{9^{\frac{1}{18}}})^{9}=(9^{\frac{1}{6}+\frac{1}{9}-\frac{1}{18}})^{9}=9^{2}=81$$
Задание 10
Перевести температуру из шкалы Цельсия в шкалу Фаренгейта позволяет формула F = 1,8∙ C + 32, где С – градусы Цельсия, F – градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 95о по шкале Фаренгейта?
Подставим в формулу значение по Фаренгейту: 95 = 1.8C + 32 и найдем отсюда С=(95-32)/1,8=35
Задание 11
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Пусть x - скорость мотоциклиста, а у - скорость велосипедиста. Пусть расстояние равно 1, минуты представим в виде часа (48/60) тогда: $$\left\{\begin{matrix} \frac{1}{y}-\frac{1}{x}=3 \\ \frac{1}{x+y}=\frac{48}{60}=\frac{4}{5} \end{matrix}\right.$$
Выразим во втором x через у:$$ x = \frac{5-4y}{4}$$ и поставим в первое: $$\frac{1}{y}-\frac{1}{\frac{5-4y}{4}}=3$$
$$\frac{1}{y}-\frac{4}{5-4y}=3$$
Приведем к общему знаменателю и найдем y: $$5-4y-4y=15y-12y^{2}$$ $$12y^{2}-23y+5=0$$
$$y_{1}=\frac{1}{4} ; y_{2}=\frac{5}{3} $$
Если подставим в x второй у, то x получится отрицательным, что нас не устраивает. Значит остается скорость велосипедиста 1/4. Значит время его будет равно : $$ \frac{1}{\frac{1}{4}} = 4$$
Задание 12
Найдите наименьшее значение функции $$f(x)=\frac{\sqrt{3}\pi }{6}-\cos x -\frac{\sqrt{3}}{2}x$$
Найдем производную этой функции: $$f'(x)=\sin x -\frac{\sqrt{3}}{2}$$
Приравняем к нулю: $$f'(x)=\sin x -\frac{\sqrt{3}}{2}=0$$
Тогда получим корни $$ x_{1}= \frac{\pi}{3}+2\pi n $$; $$ x_{2}= \frac{2\pi}{3}+2 \pi n$$
Отметим на координатной прямой данные точки и расставим знаки производной, получим, что точка минимума $$x_{1}$$ на данном промежутке соответствует $$\frac{\pi}{3}$$
Найдем значение функции в этой точке: $$f(\frac{\pi}{3})=\frac{\sqrt{3}\pi }{6}-\cos \frac{\pi}{3} -\frac{\sqrt{3}}{2}\frac{\pi}{3} =-\cos \frac{\pi }{3}=-0.5$$
Задание 14
В основании пирамиды $$PABC$$ лежит равнобедренный треугольник $$ABC$$ $$(AC=BC)$$. Все боковые ребра пирамиды попарно равны. Точка $$K$$ – середина $$AB$$. В эту пирамиду вписана сфера.
Задание 16
Дан квадрат $$ABCD$$. На сторонах $$AB$$ и $$BC$$ внешним и внутренним образом соответственно построены равносторонние треугольники $$ABK$$ и $$BCP$$.
Задание 17
Роман Абрамович внес в банк «Альфа» S тысяч рублей (S – целое число) под 10% годовых сроком на три года. Одновременно с ним Абрам Романович внес в банк «Бетта» такую же сумму на год под 15% годовых с возможностью пролонгировать (продлить) вклад на второй год под 10% годовых, а на третий – под 5% годовых. Найдите наименьшее значение S, при котором суммы на счетах Романа Абрамовича и Абрама Романовича спустя три года будут отличаться более, чем на 300 тысяч рублей.
Задание 19
Василий Кузякин возвращался из санатория домой на поезде. На перроне одной из ж/д станций продавали варёных раков: больших – по 200 руб. за штуку, средних – по 150 руб. за штуку и маленьких – по 100 руб. за штуку. Василий решил потратить на покупку раков последние пять тысяч рублей. Для себя он определил, что непременно купит и больших, и средних, и маленьких, причём их количества не будут отличаться более, чем на 2.
a) Пусть Василий купил $$x$$ штук больших раков, $$y$$ штук средних и $$z$$ штук маленьких. Тогда $$200x+150y+100z=5000$$ или 4x+3y+2z=100. При этом $$|x-y|\leq 2,|x-z|\leq 2, |z-y|\leq 2.$$ Значения $$x=11,y=12,z=10$$ удовлетворяют указанным требованиям. Да, Василий может купить раков при указанных условиях ровно на 5000 рублей.
б) Допустим, Василий сможет купить 14 больших раков при указанных условиях. Тогда $$3y+2z\leq 44$$, откуда $$y\leq \frac{44-2z}{3}$$. С учетом того, что $$y\geq z-2$$, получаем: $$z-2\leq \frac{44-2z}{3}$$; $$z\leq 10$$. Видим, что $$z$$ будет отличаться от $$x$$ более чем на 2, а это противоречит условию. Нет, Василий не сможет купить 14 раков при заданных условиях.
в) Имеем $$4x+3y+2z\leq 100.$$ С учетом $$z-x\leq 2,$$ получаем $$3x+3y+3z\leq 102;$$ $$x+y+z\leq 34;$$ Василий может купить 10 больших раков и по 12 средних и мелких, тогда общее количество раков будет максимальным, равным 34.