393 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
Решите уравнение $$\log_{1945}(x+2)=\log_{1945}(x^2-3x-10).$$
Задание 2
Грамоты призеров математического конкурса хранятся в трех коробках – по 400 грамот в первых двух, а остальные грамоты в третьей. Участник Б. приходит за своей грамотой. Найдите вероятность того, что его грамота найдется в третьей или второй коробках, если всего в конкурсе 1945 призеров. Ответ округлите до сотых.
Задание 3
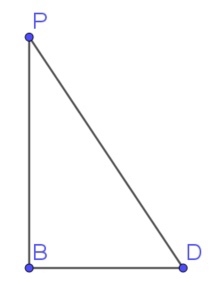
$$\ctg P=\frac{PB}{BD}=\frac{3x}{4x}\Rightarrow PD=\sqrt{(3x)^2+(4x)^2}=5x=1945\Rightarrow x=389$$
$$r=\frac{S}{p}=\frac{\frac{1}{2}\cdot PB\cdot BD}{\frac{PB+BD+PD}{2}}=\frac{\frac{1}{2}\cdot3x\cdot4x}{\frac{3x+4x+5x}{2}}=\frac{6x^2\cdot2}{12x}=x=389$$
Задание 4
Вычислите $$\frac{-4\tg137^{\circ}\cdot\tg47^{\circ}\cdot\sin1945^{\circ}}{\cos55^{\circ}}.$$
$$\frac{-4tg 137^{\circ}\cdot tg47^{\circ}\cdot\sin 1945^{\circ}}{\cos 55^{\circ}}=\frac{-4tg(90^{\circ}+47^{\circ})tg47^{\circ}\cdot\sin(1890^{\circ}+55^{\circ})}{\cos 55^{\circ}}=$$
$$=\frac{-4(-ctg47^{\circ}tg47^{\circ}\cdot\sin(1800^{\circ}+90^{\circ}+55^{\circ})}{\cos 55^{\circ}}=\frac{4\cdot1\sin(90^{\circ}+55^{\circ})}{\cos 55^{\circ}}=$$
$$\frac{4\cos 55^{\circ}}{\cos 55^{\circ}}=4$$
Задание 5
Радиус описанной окружности около правильного треугольника: $$R=\frac{\sqrt{3}}{3}a=\frac{\sqrt{3}}{3}\cdot\sqrt{3}=1$$
$$V=Sh=\pi R^2h=\pi\cdot1\cdot\frac{1945}{\pi}=1945$$
Задание 7
$$h(t)=-5t^2+18t\geq9$$
$$h(t)=-5t^2+18t-9=0$$
$$D = 18^2 - 4\cdot 5\cdot 9 = 324 - 180 = 144$$
$$t_1 = -18 + \frac{12}{-10} = 0,6$$
$$t_2 = -18 - \frac{12}{-10} = 3$$
$$3 - 0,6 = 2,4$$ (сек)
Задание 8
Пусть начальная стоимость костюма $$x$$ руб, плаща $$y$$ руб. Тогда:
$$\left\{\begin{matrix} 0,8x+0,6y=9180\\ x+y=\frac{9180}{0,68} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4x+3y=45900\\ x+y=13500 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4x+3y=45900\\ 4x+4y=54000 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow y=54000-45900=8100$$
Задание 9

График проходит через $$(-1;-1)$$ и $$(1;-2)$$. Получим:
$$\left\{\begin{matrix} -1=\log_a(b-1)\\ -2=\log_a(b+1) \end{matrix}\right.$$
$$\frac{\log_a(b+1)}{\log_a(b-1)}=\frac{-2}{-1}\Leftrightarrow\log_{b-1}(b+1)=2\Leftrightarrow\left\{\begin{matrix} (b-1)^2=b+1\\ b-1>0\\ b-1\neq1 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} b^2-3b=0\\ b>1\\ b\neq2 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow b=3$$
Тогда:
$$-1=\log_a(3-1)\Rightarrow\frac{1}{a}=2\Rightarrow a=\frac{1}{2}$$
$$\log_{0,5}(x+3)=-5\Rightarrow x=0,5^{-5}-3=29$$
Задание 10
$$P(A)=\frac{9\cdot10\cdot10\cdot10\cdot3\cdot3\cdot4}{9\cdot10\cdot10\cdot10\cdot10\cdot10\cdot10}=0,036$$
Задание 11
Найдите точку максимума функции $$y=1945+\ln(-x^2+18x+1945).$$
1) $$D(y): -x^2+18x+1945>0$$
$$x^2-18x-1945<0$$
2) $$y'=0+\frac{-2x+18}{-x^2+18x+1945}$$
3) $$y'\geq0$$
$$y'=\frac{-2x+18}{-x^2+18x+1945}\geq0$$
$$y'=\frac{-(2x-18)}{-(x^2-18x-1945)}\geq0$$
$$y'=\frac{2x-18}{x^2-18x-1945}\geq0$$
$$2x-18=\leq0$$
$$x\leq9$$
$$x_{max}=9$$