258 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 258 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №258 (alexlarin.com)
Решаем ЕГЭ 258 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №258 (alexlarin.com)
Задание 1
Диагональ экрана телевизора равна 32 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 25,4 мм. Результат округлите до целого числа сантиметров.
Задание 2
На рисунке жирными точками показана среднесуточная температура воздуха в Бухаресте каждый день с 6 по 19 июня 1992 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какого числа из указанного периода среднесуточная температура наиболее резко понизилась по сравнению с предыдущим днем.
Как видим по рисунку резкое похолодание ( в сравнении с другими днями ) произошло 15 числа
Задание 3
Клетка имеет размер 1 см*1 см. Найдите длину отрезка, соединяющего середины диагоналей трапеции АВСD. Ответ дайте в сантиметрах.
- Из $$\Delta ABC$$: $$MK=\frac{AB}{2}$$
- Из $$\Delta DBC$$: $$NM=\frac{CD}{2}$$
- $$KN=MK-NM=\frac{AB-CD}{2}=1,5$$
Задание 4
В торговом центре два разных автомата продают кофе. Вероятность того, к концу дня закончится кофе в первом автомате, равна 0,32, что закончится кофе во втором автомате – 0,24. Вероятность того, что закончится кофе в обоих автоматах, равна 0,13. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
- Вероятность того, что закончится хотя бы в одном : $$P_{1}=0,32+0,24-0,13=0,43$$
- Тогда вероятность, что останется в обоих (противоположное событие) : $$P=1-P_{1}=0,57$$
Задание 5
Найдите корень уравнения $$2\sqrt{x+1}=2-x$$ . Если корней несколько, то в ответе укажите больший из них.
$$2\sqrt{x+1}=2-x$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}(2\sqrt{x+1})^{2} =(2-x)^{2}\\2-x\geq 0\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}4(x+1)=4-4x+x^{2}\\x\leq 2\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}x^{2} -8x=0\\x\leq 2\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}\left[\begin{matrix}x=0\\x=8\end{matrix}\right.\\x\leq 2\end{matrix}\right.$$$$\Rightarrow$$$$x=0$$
Задание 6
В параллелограмме АВСD АК – биссектриса угла А, DM – биссектриса угла D. Найдите длину отрезка КМ, если известны стороны параллелограмма АВ=3, АD=5.
- $$\angle BAK=\angle KAD$$ (AK-биссектриса); $$\angle KAD=BKA$$ (накрест лежащие ) $$\Rightarrow$$ $$\Delta ABK$$ –равнобедренный ; $$AB=BK=3$$$$\Rightarrow$$ $$KC=AD-BK=2$$
- аналогично $$CD=CM=3$$$$\Rightarrow$$ $$MK=CM-KC=1$$
Задание 7
Функция y=f(x) определена на отрезке [‐2; 4]. На рисунке дан график её производной. Найдите абсциссу точки графика функции y=f(x) , в которой она принимает наименьшее значение.
При x=1 имеем , что $${f}'(x)=0$$, при этом на промежутке [-2; 1): $${f}'(x)<0$$, а на (1;4]: $${f}'>0$$$$\Rightarrow$$ $$x=1$$ - точка минимума и $$f_{min}=f(1)$$
Задание 8
Объем правильной шестиугольной призмы АВСDЕFА1В1С1D1Е1F1 равен 144. Найдите объем многогранника, вершинами которого являются точки B,E,F,F1,E1
1) $$B_{1}F_{1}\perp F_{1}E_{1}$$ и $$B_{1}F_{1}\perp FF_{1}$$$$\Rightarrow$$ $$B_{1}F_{1}$$ - высота пирамиды$$B_{1}EFF_{1}E_{1}$$ . Тогда $$V_{B_{1}EFF_{1}E_{1}}=\frac{1}{3} S_{EFF_{1}E_{1}}*B_{1}F_{1}=$$$$\frac{1}{3} *F_{1}E_{1}*B_{1}F_{1}*FF_{1}$$
2) Пусть $$F_{1}E_{1}=x; FF_{1}=h$$ . Тогда из $$\Delta F_{1}A_{1}B_{1}$$: $$F_{1}B_{1}=\sqrt{x^{2}+x^{2}-2x^{2} \cos 120}=x\sqrt{3}$$
3) Тогда $$V_{ABC..E_{1}F_{1}}=S_{AB..EF}*FF_{1}=\frac{3\sqrt{3}x^{2}}{2}*h=144$$$$\Rightarrow$$ $$\sqrt{3}x^{2}h=96$$
$$V_{B_{1}EFF_{1}E_{1}}=\frac{1}{3} *x*\sqrt{3}x*h=$$$$\frac{\sqrt{3}x^{2}h}{3}=\frac{96}{3}=32$$
Задание 9
Найдите значение выражения $$\frac{18^{12}*8^{8}}{12^{18}*3^{3}}$$
$$\frac{18^{12}*8^{8}}{12^{18}*3^{3}}=$$$$\frac{(3^{2}*2)^{12}*(2^{3})^{8}}{(2^{2}*3)^{18}*3^{3}}=$$$$\frac{3^{24}*2^{36}}{2^{36}*3^{21}}=3^{3}=27$$
Задание 10
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна $$I=\frac{\epsilon}{R+r}$$ , где ε – ЭДС источника (в вольтах), r=2,5 Ом – его внутреннее сопротивление, R – сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 25% от силы тока короткого замыкания $$I_{k3}=\frac{\epsilon}{r}$$? (Ответ выразите в омах).
Получим , что $$I=0,25 I_{kZ}=0,25 *\frac{\epsilon}{r}$$, или $$\frac{\epsilon}{R+2,5}=\frac{1}{4}*\frac{\epsilon}{2,5}$$$$\Leftrightarrow $$$$R+2,5=10\Leftrightarrow R=7,5$$
Задание 11
Имеется два сплава. Первый содержит 10% никеля, второй − 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пусть x кг –масса первого сплава, y кг - масса второго. В первом никеля 0,1 x кг, во втором : 0,3y кг. Тогда:
$$\left\{\begin{matrix}x+y=200\\0,1x+0,3y=0,25*200\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x+y=200\\0,1x+0,3y=50|*10\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x+y=200\\x+3y=500\end{matrix}\right.\Leftrightarrow$$ $$3y-y=500-200\Leftrightarrow$$ $$y=150\Rightarrow$$ $$x=50$$
Тогда 150-50=100 кг-разница
Задание 12
Найдите наименьшее значение выражения x2-x+y2-y
Рассмотрим выражение по частям : Пусть $$f(x)=x^{2}-x$$; $$g(y)=y^{2}-y$$ (функции одинаковы, следовательно, минимальные значения будут так же одинаковы) $$f_{min}=f(x_{0}); x_{0}=-\frac{-1}{2}=0,5$$$$\Rightarrow$$ $$f(x_{0})=0,5^{2}-0,5=-0,25$$ $$g(y_{0})=0,5^{2}=0,5=-0,25$$$$\Rightarrow$$ $$f_{min}+g_{min}=-0,25-0,25=-0,5$$
Задание 13
А) $$\sqrt{log_{\frac{1}{9}} ctg (\frac{2x}{9})}+\sqrt{log_{\frac{1}{9}}(\sin 4x)}=0$$$$\Leftrightarrow$$ Так как дана сумма квадратных корней, то она равна нулю только тогда, когда : $$\left\{\begin{matrix}\sqrt{log_{\frac{1}{9}}ctg\frac{2x}{9}}=0\\\sqrt{log_{\frac{1}{9}}\sin 4x}=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}log_{\frac{1}{9}}ctg\frac{2x}{9}=0\\log_{\frac{1}{9}}\sin 4x=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}ctg \frac{2x}{9}=1\\\sin 4x=1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{2x}{9}=\frac{\pi}{4}+\pi n , n \in Z\\4x=\frac{\pi}{2}+2 \pi k , k\in Z\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{9 \pi}{8}+ \frac{ 9\pi n}{2}, n \in Z\\x=\frac{\pi}{8}+\frac{\pi k}{2}, k \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=9(\frac{\pi}{8}+\frac{\pi n}{2}), n \in Z\\x=\frac{\pi}{8}+\frac{\pi k}{2}, k \in Z\end{matrix}\right.\Leftrightarrow$$ $$x=9(\frac{\pi}{8}+\frac{\pi n }{2}), n \in Z$$
Б) Рассмотрим двойное неравенство: $$\frac{3\pi}{2}\leq 9(\frac{\pi}{8}+\frac{\pi n }{2}) \leq 4\pi \Leftrightarrow$$$$\frac{1}{6}\leq \frac{1}{8}+\frac{n}{2}\leq \frac{4}{9}\Leftrightarrow$$$$\frac{1}{24}\leq \frac{n}{2}\leq \frac{23}{72}\Leftrightarrow$$$$\frac{1}{12}\leq n\leq \frac{23}{36} $$. Как видим, целых n не получили, следовательно, на данном промежутке корней нет
Задание 14
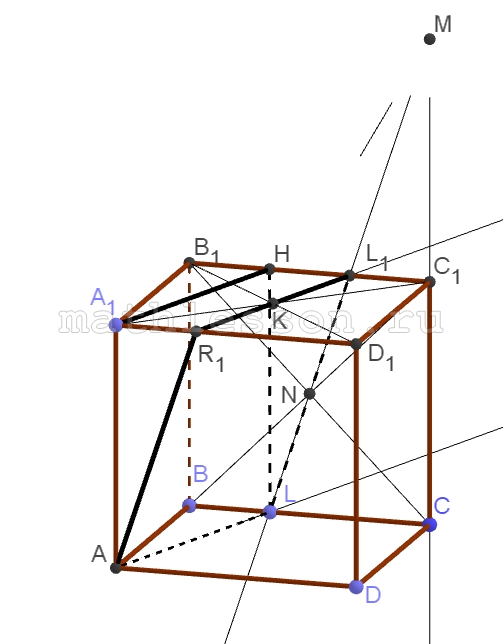
В кубе ABCDA1B1C1D1 сечение проходит через вершину А и середины граней A1B1C1D1 и B1C1CB.
A) 1) Пусть $$B_{1}D_{1}\cap A_{1}C_{1}=K$$ $$\Rightarrow$$ K - середина ($$A_{1} B_{1}C_{1}D_{1}$$). Тогда $$K \in (A_{1} C_{1} C A)$$$$\Rightarrow$$ $$AK\cap CC_{1}=M$$
2) Пусть $$B_{1}C\cap BC_{1}=N$$$$\Rightarrow$$ N - середина $$(B_{1}C_{1}CB)$$ и $$M, N \in (B_{1}C_{1}CB)$$$$\Rightarrow$$ соединяем MN, $$MN\cap B_{1}C_{1}=L_{1}$$; $$MN\cap BC=L$$
3) Соединим $$L_{1}K ; L_{1}K\cap A_{1}D_{1}=R_{1}$$$$\Rightarrow$$ $$AR_{1}L_{1}L$$ - искомое сечение
4) Рассмотрим $$\Delta AMC$$: $$KC_{1}=\frac{A_{1}C_{1}}{2}$$;. Пусть сторона квадрата равна 1, тогда:
$$A_{1}C_{1}=\sqrt{2}$$$$\Rightarrow$$ $$KC_{1}=\frac{\sqrt{2}}{2}$$; $$CC_{1}=1$$; $$\Delta MKC_{1}\sim \Delta AMC$$$$\Rightarrow$$ $$\frac{MC_{1}}{MC}=\frac{KC_{1}}{AC}$$$$\Rightarrow$$ $$MC_{1}=1$$
5) $$\Delta MCL\sim MNN_{1}(NN_{1}\left | \right |LC)$$, $$CN_{1}=\frac{1}{2}CC_{1}$$$$\Rightarrow$$ $$CN_{1}=\frac{1}{4}CM$$$$\Rightarrow$$ $$\frac{MN_{1}}{MC}=\frac{NN_{1}}{CL}=\frac{3}{4}$$; $$NN_{1}=\frac{1}{2}$$, $$LC=\frac{2}{3}$$$$\Rightarrow$$ $$BL=\frac{1}{3}$$, $$L_{1}C_{1}=\frac{1}{3}$$, $$B_{1}L_{1}=\frac{2}{3}$$
6) Пусть $$A_{1}H\left | \right |L_{1}R_{1}$$; тогда $$\Delta A_{1}B_{1}H=\Delta ABL$$$$\Rightarrow$$ $$V_{A_{1}B_{1}HABL}=\frac{1}{2}S_{ABL}*BB_{1}=\frac{1}{2} *1*\frac{1}{3}*1=\frac{1}{6}$$
7) $$\Delta A_{1}AR_{1}=HLL_{1}$$$$\Rightarrow$$ $$V_{A_{1}R_{1}ALHL_{1}}=S_{AA_{1}R_{1}}*h$$, где h - высота призмы $$A_{1}R_{1}ALHL_{1}$$; $$A_{1}B_{1}(A_{1}B_{1}\perp (B_{1}C_{1}CB))$$$$\Rightarrow$$ $$V_{A_{1}R_{1}ALHL_{1}}=\frac{1}{2}*1*\frac{1}{3}*1=\frac{1}{6}$$
Тогда $$V_{A_{1}B_{1}L_{1}R_{1}ABL}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}=V_{1}$$; $$V_{ABCDA_{1}B_{1}C_{1}D_{1}}=1^{3}=1$$$$\Rightarrow$$ $$V_{ALCDR_{1}L_{1}C_{1}D_{1}}=\frac{2}{3}=V_{2}$$ ;$$\frac{V_{1}}{V_{2}}=\frac{1}{3}:\frac{2}{3}=\frac{1}{2}$$
Б) введем ортогальную систему координат: $$A(0;1;0)$$; $$R_{1}(0;\frac{2}{3};1)$$; $$L(1; \frac{2}{3}; 0)$$. Зададим уравнение ($$ALL_{1}R_{1}$$): $$\left\{\begin{matrix}0*a+1*b+0*c+d=0\\0*a+\frac{2}{3} b+1*c+d=0\\1*a+\frac{2}{3}b+0*c+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}b=-d\\a=-\frac{d}{3}\\c=-\frac{d}{3}\end{matrix}\right.$$$$\Rightarrow$$ $$(ALL_{1}R_{1})$$:$$-\frac{1}{3}x-1*y-\frac{1}{3}z+1=0$$ и нормаль-вектор к этой плоскости: $$\bar{n}(-\frac{1}{3},-1,-\frac{1}{3})$$. Нормаль-вектор к (ABCD): $$\tilde{m} (0,0,1)$$ (ось OZ): тогда косинус угла м\у ($$ALL_{1}R_{1}$$) и (ABCD) равен $$\cos (\bar{m}, \bar{n})$$:
$$\cos (\bar{m}, \bar{n})=\frac{\left | -\frac{1}{3}*0+(-1)*0+(-\frac{1}{3})*1 \right |}{\sqrt{(-\frac{1}{3})^{2}+(-1)^{2}+(-\frac{1}{3})^{2}} \sqrt{0^{2}+0^{2}+1^{2}}}=\frac{1}{\sqrt{11}}$$$$\Rightarrow$$ $$\angle (\bar{m}, \bar{n})=arccos \frac{1}{\sqrt{11}}$$
Задание 15
Решите неравенство $$\log_{x} (x+\frac{1}{3}) \leq \log_{\sqrt{2x+3}} (x+\frac{1}{3})$$
$$\log_{x} (x+\frac{1}{3})\leq \log_{\sqrt{2x+3}}(x+\frac{1}{3})$$
ОДЗ: $$\left\{\begin{matrix}x+\frac{1}{3}>0\\x>0\\2x+3>0\\x\neq 1\\2x+3\neq 1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>-\frac{1}{3}\\x>0\\x>-1,5\\x\neq 1\\x-1\end{matrix}\right.\Leftrightarrow$$ $$x \in (0;1)\cup (1; +\infty )$$
Решение : воспользуемся формулой : $$\log_{g}f=\frac{1}{\log_{f}g}$$
$$\frac{1}{\log_{(x+\frac{1}{3})}x}\leq \frac{1}{\log_{(x+\frac{1}{3})\sqrt{2x+3}}}$$$$\Leftrightarrow$$$$\frac{\log_{(x+\frac{1}{3})}\sqrt{2x+3}-\log_{(x+\frac{1}{3})}x}{\log_{(x+\frac{1}{3})}x*\log_{(x+\frac{1}{3})}\sqrt{2x+3}}\leq 0$$$$\Leftrightarrow$$$$\frac{\log_{(x+\frac{1}{3})}\frac{\sqrt{2x+3}}{x}}{\log_{(x+\frac{1}{3})}x*\log_{(x+\frac{1}{3})}\sqrt{2x+3}}\leq 0$$ $$\Leftrightarrow$$ $$\log_{x} \frac{\sqrt{2x+3}}{x}*\log_{\sqrt{2x+3}}(x+\frac{1}{3})\leq 0$$$$\Leftrightarrow$$ $$(\frac{\sqrt{2x+3}}{x}-1)(x-1)(x+\frac{1}{3}-1)(\sqrt{2x+3}-1)\leq 0$$$$\Leftrightarrow$$ $$\frac{\sqrt{2x+3}-x}{x}(x-1)(x-\frac{2}{3})(2x+3-1)\leq 0$$
Рассмотрим $$\sqrt{2x+3}-x$$. С учетом ОДЗ: $$\sqrt{2x+3}-x$$$$\Leftrightarrow$$ $$2x+3-x^{2}$$$$\Leftrightarrow$$ $$-(x-3)(x+1)$$. Получим : $$\frac{-(x-3)(x+1)(x-1)(x-\frac{2}{3})(2x+2)}{x}\leq 0$$$$\Leftrightarrow$$ $$\frac{(x+1)^{2}(x-1)(x-\frac{2}{3})(x-3)}{x}\geq 0$$
С учетом ОДЗ : $$(x+1)^{2}$$ можно убрать (поделить на него): $$\frac{(x-1)(x-\frac{2}{3})(x-3)}{x}\geq 0$$$$\Leftrightarrow$$ $$\left[\begin{matrix}x\geq 3\\\left\{\begin{matrix}x\geq \frac{2}{3}\\x<1\end{matrix}\right.\\x<0\end{matrix}\right.$$
Но т.к. $$x>0$$ , то $$x \in [\frac{2}{3};1)\cup [3; +\infty )$$
Задание 16
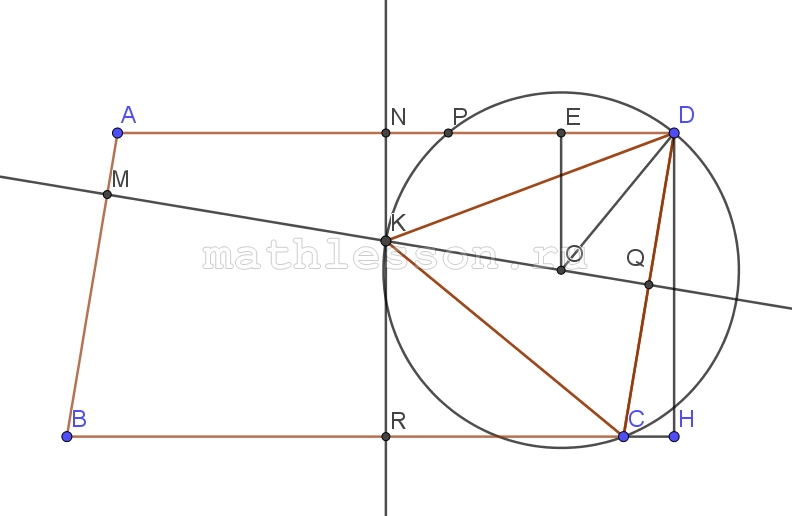
Внутри параллелограмма ABCD взята точка К так, что треугольник CKD равносторонний. Известно, что расстояния от точки К до прямых AD, AB и ВС равны соответственно 3, 6 и 5.
A) Пусть $$CD=KD=KC=a$$, тогда из $$\Delta NKD$$ : $$ND=\sqrt{a^{2}-3^{2}}$$; Из $$\Delta KRC$$: $$RC=\sqrt{a^{2}-5^{2}}$$
2) Пусть $$DH\perp BC$$ , тогда $$DH=NR=8$$; $$CH=ND=RC=\sqrt{a^{2}-3^{2}}-\sqrt{a^{2}-5^{2}}$$. $$\Delta DHC$$: $$a^{2}=8^{2}+(\sqrt{a^{2}-3^{2}}-\sqrt{a^{2}-5^{2}})^{2}\Leftrightarrow$$$$a^{2}-8^{2}=2a^{2}-34-2\sqrt{a^{4}-34a^{2}+225}\Leftrightarrow$$$$2\sqrt{A^{4}-34a^{2}+225}=a^{2}+30\Leftrightarrow$$$$4a^{4}+136a^{2}+900=a^{4}+60a^{2}+900\Leftrightarrow$$$$3a^{4}-196 a^{2}=0$$. Тогда a=0(не может быть) член $$a=\pm \frac{14\sqrt{3}}{3}$$ ( отрицательным не может быть )
3) $$KQ=CD \sin 60$$; $$CD=\sqrt{DH^{2}+CH^{2}}=\sqrt{64+((\sqrt{\frac{14^{2}}{3}-9}-\sqrt{(\frac{14^{2}}{3}-25)})^{2}}=$$$$\sqrt{64+(\frac{13}{\sqrt{3}}-\frac{11}{\sqrt{3}})^{2}}=\sqrt{\frac{196}{3}}=$$$$\frac{14}{\sqrt{3}}\Rightarrow$$ $$KQ=\frac{14}{\sqrt{3}}*\frac{\sqrt{3}}{2}=7$$$$\Rightarrow$$ $$MQ=13$$
4) $$S_{ABCD}=MQ*CD=13*\frac{14}{\sqrt{3}}=\frac{182}{\sqrt{3}}$$
Б) 1) из $$\Delta CHD$$: $$\sin \angle DCH=\frac{DH}{CD}=\frac{8}{\frac{14}{\sqrt{3}}}=\frac{4\sqrt{3}}{7}$$$$\Rightarrow$$ $$\sin \angle ADC=\frac{4\sqrt{3}}{7}=\sin \alpha$$
2) $$\angle ODQ=\frac{1}{2} \angle KDC=30$$$$\Rightarrow$$ $$\angle PDO=\angle (\alpha -30)$$, где $$\angle \alpha =\angle ADC$$; $$\cos \alpha =\sqrt{1-\sin ^{2}\alpha }=\frac{1}{7}$$; $$\sin (\alpha -30)=\sin \alpha \cos 30-\cos \alpha \sin 30=$$$$\frac{4\sqrt{3}}{7}*\frac{\sqrt{3}}{2}-\frac{1}{7}*\frac{1}{2}=$$$$\frac{11}{14}\Rightarrow$$ $$\cos(\alpha -30)=\frac{5\sqrt{3}}{14}$$
3) OD - радиус описанной окружности $$\Rightarrow$$ $$OD=\frac{2}{3}$$; $$KQ=\frac{2*7}{3}=\frac{14}{3}$$$$\Rightarrow$$ из $$\Delta EDO$$: $$ED=DO \cos PDO=\frac{14}{3}*\frac{5\sqrt{3}}{14}=$$$$\frac{5\sqrt{3}}{3}\Rightarrow$$ $$PD=\frac{10\sqrt{3}}{3}$$
4) $$S_{ABCD}=\frac{182}{\sqrt{3}}=AD*DH\Rightarrow$$ $$AD=\frac{182}{\sqrt{3}*8}=\frac{91}{4\sqrt{3}}\Rightarrow$$ $$AP=\frac{91}{4\sqrt{3}}-\frac{10}{\sqrt{3}}=\frac{51}{4\sqrt{3}}$$, $$\frac{AP}{AD}=\frac{51}{4\sqrt{3}}:\frac{91}{4\sqrt{3}}=\frac{51}{91}$$
Задание 17
Вновь созданное акционерное общество продало населению 1000 своих акций, установив скидку 10% на каждую пятую продаваемую акцию и 25% на каждую тринадцатую продаваемую акцию. В случае, если на одну акцию выпадают обе скидки, то применяется большая из них. Определите сумму, вырученную от продажи всех акций, если цена акции составляет 1000 рублей.
Всего акций n=1000. При этом под «каждую пятую» попадает $$m=\frac{1000}{5}=200$$ акций, под каждую 13: $$h =\frac{1000}{13}\approx 76$$ акций
При этом, так как 5 и 13 взаимопростые , то из 76 в каждой пятерке номеров один так же будет попадать в «каждую пятую» $$\frac{76}{5}\approx 15$$. Получим, что со скидкой 10% : 200-15=185 акций (так как на 15 штук будет браться большая скидка - они попадают так же под 13-е). Со скидкой 25% : 76 шт., без скидки: 1000-185-76=739 шт. Тогда выручка: $$S=739*1000+185*900+76*750=962500$$
Задание 18
При каких значениях параметра a уравнение $$(a-1)4^{x}+(2a-3)6^{x}=(3a-4)9^{x}$$ имеет единственное решение?
$$(a-1)*4^{x}+(2a-3)*6^{x}=(3a-4)*9^{x}|:3^{2x}\Leftrightarrow$$$$(a-1)(\frac{2}{3})^{2x}+(2a-3)(\frac{2}{3})^{x}-(3a-4)=0$$
Пусть: $$(\frac{2}{3})^{x}=y>0$$
$$(a-1) *y^{2}+(2a-3)y-(3a-4)=0$$
$$D=(2a-3)^{2}+4(a-1)(3a-4)=16a^{2}-40a+25=(4a-5)^{2}$$
$$y_{1}=\frac{3-2a+\left | 4a-5 \right |}{2(a-1)}$$
$$y_{2}=\frac{3-2a-\left | 4a-5 \right |}{2(a-1)}$$
Существуют следующие варианты единственного решения :
1) $$y_{1}=y_{2}\Rightarrow$$ $$4a-5=0\Rightarrow$$ $$a=\frac{5}{4}$$. Выполним проверку: $$(\frac{2}{3})^{x}=\frac{3-2,5}{2(1,25-1)}=1\Rightarrow$$ $$x=0$$ - один корень
2) Один из корней меньше или равен 0 , второй больше 0. Сравним корни: $$\frac{3-2a+\left | 4a-5 \right |}{2(a-1)}>\frac{3-2a-\left | 4a-5 \right |}{2(a-1)}$$$$\Leftrightarrow$$ $$\frac{2\left | 4a-5 \right |}{2(a-1)}>0$$$$\Leftrightarrow$$ $$\frac{\left | 4a-5 \right |}{a-1}>0$$$$\Rightarrow$$
При $$a>1: y_{1}>y_{2}$$;
При $$a<1 : y_{2}>y_{1}$$,
Тогда решение будет при условии: $$\left[\begin{matrix}\left\{\begin{matrix}a>1\\y_{2}\leq 0& &\end{matrix}\right.(1)\\\left\{\begin{matrix}a<1\\y_{1}\leq 0\end{matrix}\right. (2)\end{matrix}\right.$$
Рассмотрим системы отдельно:
(1): $$\left\{\begin{matrix}a>1\\\frac{3-2a-\left | 4a-5 \right |}{a-1}\leq 0 & &\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}a>1\\\left | 4a-5 \right |\geq 3-2a\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a>1\\\left[\begin{matrix}4a-5\geq 3-2a\\4a-5\leq 2a-3\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a>1\\\left[\begin{matrix}a\geq \frac{4}{3}\\a\leq 1\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$a \in [\frac{4}{3}; +\infty )$$
(2): $$\left\{\begin{matrix}a<1\\\frac{3-2a+\left | 4a-5 \right |}{2(a-1)} \leq 0\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a<1\\3-2a+\left | 4a-5 \right |\geq 0\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}a<1\\\left | 4a-5 \right |\geq 2a-3\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}a<1\\\left[\begin{matrix}4a-5\geq 2a-3\\4a-5\leq 3-2a\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$$$\left\{\begin{matrix}a<1\\\left[\begin{matrix}a\geq 1\\a\leq \frac{4}{3}\end{matrix}\right.\end{matrix}\right.$$$$\Leftrightarrow$$ $$a<1$$
Проверим случай $$a=1$$: $$-6^{x}=-9^{x}\Rightarrow$$ $$x=0$$ - один корень
Тогда конечный ответ: $$a \in (-\infty ;1]\cup {\frac{5}{4}}\cup [\frac{4}{5}; +\infty )$$
Задание 19
На волшебной яблоне выросли 15 бананов и 20 апельсинов. Одновременно разрешается срывать один или два плода. Если сорвать один из плодов вырастет такой же, если сорвать сразу два одинаковых плода – вырастет апельсин, а если два разных – вырастет банан.
19) A) Если сорвать 1 шт. , то вырастет такой же , т.е. общее число не меняется. Тогда срываем по 2. Пусть Sx=15 число бананов,Sy=20-число апельсинов.
-если срываем 2 одинаковых, то будет -2x и + y (если 2 банана) или – y(если 2 апельсина)
-если 2 разных, то – y.
Тогда будем срывать сначала 2 банана 7 раз и получим : $$S_{x}=15-7*2=1$$ банан и $$S_{y}=20+7*1=27$$ апельсинов
А потом 26 раз по 2 апельсина: $$S_{x}=1$$ банан ; $$S_{y}=27-26*1=1$$ – апельсин. И оба плода, тогда: $$S_{x}=1$$ и $$S_{y}=0$$
Б) из п. A это будет банан.
B) Нет, так как изначально имеем нечетное количество бананов, следовательно, убирая по 2 банана в итоге в остатке получим 1 банан (других вариантов, кроме как убрать 2 банана, нет) . А далее мы в любом случае будем его получать, уменьшая Sy до 0 апельсинов.