235 вариант Алекса Ларина. Разбор ЕГЭ математика 2018.
Решаем ЕГЭ 235 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №235 (alexlarin.com)
Решаем ЕГЭ 235 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №235 (alexlarin.com)
Задание 1
Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?
Пусть $$3500-100$$% снизили на $$700-x$$%; $$x=\frac{700\cdot100}{3500}=20$$
Задание 2
На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов. На оси абсцисс откладывается число оборотов в минуту, по оси ординат – крутящий момент в Н∙м
Чтобы преодолеть глубокий снег, водителю требуется максимальный крутящий момент двигателя. Какое наименьшее число оборотов в минуту должен поддерживать водитель этой машины?
Задание 3
Площадь параллелограмма ABCD равна 12. Точки Е и F – середины сторон соответственно АВ и CD. Найдите площадь параллелограмма AECF.
$$AE=\frac{1}{2}AB$$ $$\Rightarrow$$ $$S_{AEF}=\frac{1}{2}S_{ABCD}=6$$
Задание 4
Дан правильный пятиугольник. Учитель предлагает ученику выбрать наугад две вершины. Найдите вероятность того, что выбранные вершины принадлежат одной стороне пятиугольника.
Рядом с вершиной есть 2 другие и 2 на на одной стороне с ней: $$P=\frac{2}{4}=0,5$$
Задание 5
В треугольнике ABC известно, что угол $$C=90^{\circ}$$, а медиана CM и биссектриса AL пересекаются в точке T, причём CT = CL. Найдите наибольший острый угол треугольника ABC. Ответ дайте в градусах.
Пусть $$\angle MCB=\alpha$$, т.к. $$CM=MB$$ (свойство медианы прямоугольного треугольника) $$\angle MCB=\alpha$$ $$\Rightarrow$$ $$\angle CAB=90^{\circ}-\alpha$$ $$\Rightarrow$$ $$\angle CAL=45^{\circ}-\frac{\alpha}{2}$$; $$\angle CLT=\angle CTL=\frac{180^{\circ}-\alpha}{2}=90^{\circ}-\frac{\alpha}{2}$$
Тогда из $$\bigtriangleup ACL$$: $$45^{\circ}-\frac{\alpha}{2}+90^{\circ}+90^{\circ}-\frac{\alpha}{2}=180$$; $$45^{\circ}-\alpha=0$$; $$\alpha=45^{\circ}$$
Задание 7
Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Высота нижней тогда составяет $$\frac{2}{3}$$ от высоты исходной. Т.к. основания одинаковы, то и объем $$\frac{2}{3}$$ от исходной: $$V=\frac{2}{3}\cdot15=10$$
Задание 8
Найдите значение выражения $$\frac{f(x-7)}{f(x-6)}$$, если $$f(x)=5^{x}$$
$$\frac{f(x-7)}{f(x-6)}=\frac{5^{x-7}}{5^{x-6}}=\frac{1}{5}=0,2$$
Задание 9
Напряжение, выраженное в вольтах, на участке цепи постоянного тока с сопротивлением R (в Омах) выражается по формуле $$U=\sqrt{\frac{50AR}{3t}}$$, где А - работа в кДж(килоджоулях), совершенная за время t минут. Какую максимальную работу совершает электрический ток в пылесосе, если при напряжении 120 вольт сопротивление равно 1200 Ом, а технические характеристики этого участка цепи постоянного тока позволяют включить пылесос на время не более 2 минут? Ответ запишите в килоджоулях.
$$A=\frac{U^{2}\cdot3t}{50R}$$; $$A=\frac{120^{2}\cdot3\cdot2}{50\cdot1200}=$$ $$\frac{120\cdot120\cdot3\cdot2}{50\cdot1200}=1,44$$
Задание 10
Два пешехода вышли одновременно из пунктов А и В навстречу друг другу. Когда первый прошел половину пути, второму до конца пути оставалось еще 24 км. Когда второй прошел половину пути, первому до конца оставалось еще 15 км. Сколько километров останется пройти второму до А после того, как первый дойдет из А в В?
Пусть S - общее расстояние, х - скорость первого (тогда время до середины $$\frac{S}{2x}$$); у - скорость второго (его время до середины $$\frac{S}{2y}$$): $$\left\{\begin{matrix}\frac{S}{2x}\cdot y=S-24\\\frac{S}{2y}\cdot x=S-15\end{matrix}\right.$$ Умножим первое на второе: $$(S-24)(S-15)=\frac{S^{2}}{4}$$;
$$S^{2}-39S+360-\frac{S^{2}}{4}=0$$ $$|\cdot\frac{4}{3}$$
$$S^{2}-52S+480=0$$
$$\left\{\begin{matrix}S_{1}+S_{2}=52\\S_{1}\cdot S_{2}=480\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}S_{1}=40\\S_{2}=14\end{matrix}\right.$$
$$S_{2}$$ не может быть, т.к. $$S-24>0$$. Подставим $$S$$ в первое уравнение: $$\frac{40}{2x}\cdot y=40-24$$; $$\frac{20y}{x}=16$$ $$\Rightarrow$$ $$16x=20y$$ $$\Rightarrow$$ $$x=1,25y$$ или $$y=\frac{4}{5}x$$
Время, за которое первый пройдет $$S$$: $$t=\frac{S}{1,25y}$$. Тогда расстояние, которое пройдет второй за это время: $$S_{1}=\frac{S}{1,25y}\cdot y=\frac{S}{1,25}=\frac{40}{1,25}=32$$
Значит останется : $$40-32=8$$
Задание 11
Найдите наибольшее значение функции $$y=\frac{250+50x-x^{3}}{x}$$ на отрезке $$[-10;-1]$$
$$y=\frac{250+50x-x^{3}}{x}$$; $$y'=\frac{(50-3x^{2})x-(250+50x-x^{3})}{x^{2}}=$$ $$\frac{50x-3x^{3}-250-50x+x^{3}}{x^{2}}=$$ $$\frac{-2x^{3}-250}{x^{2}}=0$$; $$x^{3}=-125$$ $$\Rightarrow$$ $$x=-5$$;
$$y(-5)=\frac{250+50\cdot(-5)-(-5)^{3}}{(-5)}=\frac{125}{-5}=-25$$
Задание 12
А) Решите уравнение $$\frac{5}{\cos^{2}(\frac{13\pi}{2}-x)}+\frac{7}{\sin x}-6=0$$;
Б) Найдите все корни этого уравнения, принадлежащие промежутку $$[\frac{3\pi}{2};3\pi]$$
А) $$\frac{5}{\cos^{2}(\frac{13\pi}{2}-x)}+\frac{7}{\sin x}-6=0$$; $$\left\{\begin{matrix}\cos^{2}(\frac{13\pi}{2}-x)\neq0\\\sin x\neq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\sin^{2}x\neq0\\\sin x\neq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$x\neq\pi n,n\in Z$$
$$\frac{5}{\sin^{2}x}+\frac{7}{\sin x}-6=0$$
Замена: $$\frac{1}{\sin x}=y$$
$$5y^{2}+7y-6=0$$;
$$D=49+120=13^{2}$$;
$$y_{1}=\frac{-7+13}{10}=\frac{6}{10}$$;
$$y_{2}=\frac{-7-13}{10}=-2$$
$$\left\{\begin{matrix}\frac{1}{\sin x}=-2\\\frac{1}{\sin x}=\frac{6}{10}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\sin x=-\frac{1}{2}\\\sin x=\frac{10}{6}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=(-1)^{n+1}\frac{\pi}{6}+\pi n,n\in Z\\ \varnothing \end{matrix}\right.$$
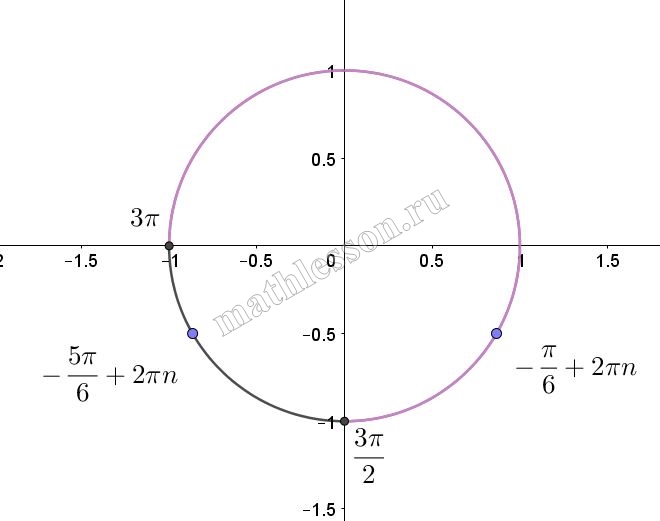
Б)Построим единичную окружность, отметим полученные корни и заданный промежуток:
Как видим, на заданном промежутке есть только корень $$\frac{\pi}{6}+2\pi n$$. Найдем его значение: $$2\pi- \frac{\pi}{6}=\frac{11\pi}{6}$$
Задание 13
В правильной шестиугольной призме $$ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}$$ стороны основания равны 4, а боковые ребра 5.
a) 1) $$A_{1}$$ и $$C_{1}$$ соединяем . Пусть $$A_{1} C_{1} \cap E_{1} F_{1}=K$$, тогда E и K соединяем; $$EK\cap FD_{1}=M$$
Пусть $$A_{1} C_{1} \cap E_{1} F_{1}=R\Rightarrow ER\cap FF_{1}=N\Rightarrow (A_{1}NEMC_{1})$$- искомая $$(A_{1}C_{1}E)$$
2) $$E_{1}B_{1}\cap A_{1}C_{1}=H\Rightarrow EH$$-линия пересечения $$(A_{1}C_{1}E)$$ и $$(BB_{1}E_{1}E)$$
3) $$A_{1}C_{1}\perp E_{1}B_{1}$$(т.к. в основании правильной призмы) ,но $$A_{1}C_{1}\perp BB_{1}$$( т.к. призма правильная) $$\Rightarrow (A_{1}C_{1}E)\perp (BB_{1}E_{1}E)$$
b) 1)Отпустим $$HH_{1}\perp (ABCDEF)\Rightarrow HH_{1}=AA_{1}=5$$
2)Пусть O-центр основания $$\Rightarrow OE=AB=4$$
3) AOCB- ромб (OC=BC=AB=AO; $$\angle AOC=\angle ABC$$)$$\Rightarrow OH_{1}-H_{1}B=\frac{1}{2}OB=2$$
4) $$tg \angle HEH_{1}=\frac{HH_{1}}{EH_{1}}=\frac{5}{6}\Rightarrow \angle HEH_{1}-arctg\frac{5}{6}$$
Задание 14
Решите неравенство $$\log_{64x}4\cdot\log^{2}_{0,5}(8x)\leq3$$
$$\log_{64x}4*\log_{0,5}^{2}(8x)\leq 3$$
ОДЗ: $$\left\{\begin{matrix}64x>0\\64x\neq 1\\8x>0 \end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x>0\\x \neq \frac{1}{64}\\\end{matrix}\right.$$$$x\in (10 \frac{1}{64})\cup (\frac{1}{64}+\infty)$$
$$\frac{1}{\log_{4}64} +\log_{2}^{2}(8x)\leq 3\Leftrightarrow$$$$\frac{1}{\log_{4}64+\log_{4}x}*(\log_{2}8+\log_{2}x)^{2}\leq 3\Leftrightarrow$$$$\frac{1}{3+\frac{1}{2}\log_{2}x}*(3+\log_{2}x)^{2}\leq 3$$
Замена $$\log_{2}x=y$$
$$\frac{1}{3+0,5 y}(3+y)^{2}-3\leq 0\Leftrightarrow$$$$\frac{9+6y+y^{2}-9-1,5y}{3+0,5 y}\leq 0\Leftrightarrow \frac{y^{2}+4,5 y}{0,5y+3}\leq 0\Leftrightarrow$$$$\frac{y(y+4,5)}{0,5y+3}\leq 0\Leftrightarrow$$
$$\left\{\begin{matrix}y<-6\\\left\{\begin{matrix}y\geq -4,5\\y\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}\log_{2}x<-6\\\left\{\begin{matrix}\log_{2}x\geq -4,5\\log_{2}x\leq 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow $$$$\left\{\begin{matrix}x<\frac{1}{64}\\\left\{\begin{matrix}x\geq \frac{1}{\sqrt{512}}\\x\leq 1\end{matrix}\right.\end{matrix}\right.$$
С учетом ОДЗ:
$$x\in (0 ;\frac{1}{64})\cup [\frac{1}{16\sqrt{2}};1]$$
Задание 15
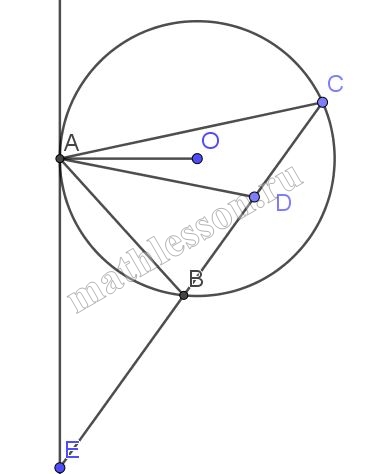
Касательная в точке $$A$$ к описанной окружности треугольника $$ABC$$ пересекает прямую $$BC$$ в точке $$E$$, $$AD$$ – биссектриса треугольника $$ABC$$.
A) 1) $$\angle ACB$$-вписанный $$\Rightarrow \angle ACB=\frac{1}{2}\cup AB$$; $$\angle AEB$$-между касательной и хордой $$\Rightarrow \angle AEB=\frac{1}{2}\cup AB\Rightarrow \angle ACB=\angle AEB.$$
2) AD-биссектриса $$\Rightarrow \angle CAD=\angle BAD$$; $$\angle EAD=\angle AEB+\angle BAP(1)$$; $$\angle ADE=\angle ACB+\angle CAP(2)$$
Из (1)и(2), $$\angle EAP=\angle ADE\Rightarrow EA=ED$$
Б) 1) $$\Delta AEB\sim \Delta EAC(\angle E$$- общий;$$\angle EAB=\angle ACE$$)
$$\frac{AB}{AC}=\frac{EB}{EA}=\frac{EA}{EC}(3)$$. Тогда $$EA^{2}=EB*EC$$; $$EA=\sqrt{9*4}=6$$
2) По теореме косинусов из $$\Delta EAB$$: $$AB=\sqrt{4^{2}+6^{2}-2*4*\frac{9}{16}}=5$$
3) из равенства (3): $$\frac{AB}{AC}=\frac{EB}{EA}\Leftrightarrow AC=\frac{AB*EA}{EB}=\frac{5*6}{4}=\frac{15}{2}$$
4) BC=EC-EB=5, тогда : $$AB=BC \Rightarrow$$ расстояние от B до AC-высота BH: $$BH=\sqrt{BC^{2}-(\frac{1}{2}AC)^{2}}=\sqrt{25-(\frac{15}{4})^{2}}=\sqrt{\frac{175}{16}}=\frac{5\sqrt{7}}{4}$$ Ответ :$$\frac{5\sqrt{7}}{4}$$
Задание 16
Аристарх Луков‐Арбалетов хочет купить пакет акций быстрорастущей компании. В начале года у Аристарха совсем не было денег, а пакет стоил 100 000 рублей. В середине каждого месяца Аристарх откладывает на покупку пакета акций одну и ту же сумму, а в конце каждого месяца пакет дорожает на 20%. Какую наименьшую сумму нужно откладывать Аристарху каждый месяц, чтобы через некоторое время купить вожделенный пакет акций?
Пусть x–сумма , которую откладывает , n- число месяцев, через которое отложенная сумма станет не меньше стоимости пакета: $$10^{5}*1,2^{n-1}\leq xn$$ $$n-1$$ Т.к. сначала он отложит и только потом зачислится процент $$x\geq \frac{10^{5}*1,2^{n-1}}{n}$$ Найдем минимум этой функции относительно n : $$(\frac{10^{5}*1,2^{n-1}}{n})^{1}=10^{5}\frac{n*1,2^{n-1}*\ln1,2-1,2^{n-1}}{n^{2}}=0\Leftrightarrow$$$$1,2^{n-1}(n*\ln1,2-1)=0\Leftrightarrow$$$$\ln 1,2^{n}=1\Leftrightarrow$$$$\ln 1,2^{n}=\ln e\Leftrightarrow$$$$1,2^{n}=e$$, следовательно, $$n \in [5; 6]$$. Найдем значения на концах данного промежутка: $$x(5)=\frac{10^{5}*1,2^{4}}{5}=41472$$ $$x(6)=\frac{10^{5}*1,2^{5}}{6}=41472$$
Задание 17
Найдите все значения параметра , при каждом из которых уравнение $$(x^{2}-5+\ln(x+a))^{2}=(x^{2}-5)^{2}+\ln^{2}(x+a)$$ имеет единственное решение на отрезке $$[0;3]$$
$$(x^{2}-5+\ln(x+a))^{2}=(x^{2}-5)^{2}+\ln^{2}(x+a)$$
ОДЗ: $$x+a>0 \Leftrightarrow x>-a$$
$$(x^{2}-5)^{2}+2(x^{2}-5)\ln^{2}(x+a)=(x^{2}-5)^{2}+\ln^{2}(x-a)$$
$$(x^{2}-5)\ln(x-a)=0$$
$$\left\{\begin{matrix}x^{2}-5=0 \\\ln(x+a)=0 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x_{1}=\pm \sqrt{5} \\x_{2}=1-a \end{matrix}\right.$$
$$\sqrt{5}\in [0; 3]$$, тогда есть три возможных варианта ($$x_{2}\in$$ ОДЗ при всех a)
1) $$x_{1}\notin$$ ОДЗ и $$x_{2}\in [0 ;3]$$
$$\left\{\begin{matrix}\sqrt{5}\leq -a \\0\leq1-a\leq 3 \end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a\leq -\sqrt{5} \\-2\leq \leq 2\end{matrix}\right.\Leftrightarrow$$ $$\varnothing$$
2) $$x_{1}\in$$ ОДЗ и $$x_{2}\notin [0 ;3]$$
$$\left\{\begin{matrix}\sqrt{5}>- a \\\left\{\begin{matrix}1-a>3 \\1-a<0 \end{matrix}\right. \end{matrix}\right.\Leftrightarrow$$
$$\left\{\begin{matrix}a>-\sqrt{5} \\\left\{\begin{matrix}a<-2 \\a>1 \end{matrix}\right. \end{matrix}\right.\Leftrightarrow$$$$a\in (-\sqrt{5};-2)\cup (1; +\infty )$$
3) $$x_{1}=x_{2}$$
$$1-a=\sqrt{5}\Leftrightarrow 1-\sqrt{5}$$
Объединим полученные результаты: $$a\in (-\sqrt{5};-2)\cup (1-\sqrt{5})\cup (1; +\infty)$$
Задание 18
По результатам теста по математике ученик получает неотрицательное число баллов. Ученик войдет в группу А, если количество баллов не менее 45. Если количество баллов меньше 45, то ученик войдет в группу Б. Чтобы не расстраивать родителей, решили каждому ученику добавить 8 баллов, поэтому количество учеников группы А увеличилось.
A) Пусть было 3 человека : 100;44;0. Тогда в Б был средний $$\frac{44+0}{2}=22$$ , а после прибавки в Б остался один человек с баком 8 $$\Rightarrow$$ понизился. Да
Б) Из пункта а) в группе А был один человек с баком 100,стало 2 и их средний: $$\frac{100+44+8*2}{2}=80$$. Т.е. понизился. Да.
В) Всего было N человек. В группе А сначала x $$\Rightarrow$$ в Б: N-x; стало в А: y, тогда в Б: N-y. Средний бал всех после добавлений станет: 46+8=54. Тогда:
$$\left\{\begin{matrix}46N=34(N-x)+52x\\54N=38(N-y)+58y\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}12N=18x\\16N=20y\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{2N}{3}\\y=\frac{4N}{5}\end{matrix}\right.$$
X ;y; N-числа натуральные, значит делится нацело на 3 и 5 $$\Rightarrow N=15.$$