309 вариант Алекса Ларина. Разбор ЕГЭ математика 2020.

В бидон налили 4 литра молока трехпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?

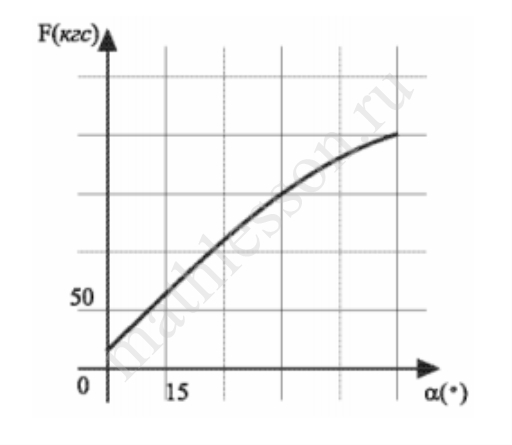
В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат – сила натяжения транспортерной ленты (в килограммах силы). Определите по рисунку, чему (в кгс) равна сила натяжения транспортерной ленты при угле наклона 45⁰?

Найдите площадь трапеции ABCD. Размер клетки 1см х 1см. Ответ дайте в квадратных сантиметрах.

На пяти карточках написаны цифры 1, 2, 3, 4, 5. Вынимается одна карточка, стоящее на ней число записывается, карточка возвращается обратно. Карточки перемешиваются, затем вынимается еще одна карточка, стоящее на ней число записывается. Найдите вероятность того, что второе записанное число больше первого.

Решите уравнение: $$\sqrt{(3-6x)^2}+\sqrt{(6+6^{x})(36-6^{x})}=6^{x}-3$$

Дан ромб ABCD с острым углом B. Площадь ромба равна 320, а синус угла В равен 0,8. Высота СН пересекает диагональ BD в точке К. Найдите длину отрезка СК.

Найдите значение функции $$y=\frac{3f(x)-2f(-x)}{2g(x)-3g(-x)}$$ в точке x₀, если известно, что функция $$y=f(x)$$ четная, функция $$y=g(x)$$ нечетная, $$f(x_0)=5$$, $$g(x_0)=1$$

Расстояние между серединами ребер ВС и С₁D₁ куба ABCDA₁B₁C₁D₁ равно 6 . Найдите объем куба.

Найдите значение выражения $$(\sqrt[3]{4}-\sqrt[3]{3})(\sqrt[3]{16}+\sqrt[3]{12}+\sqrt[3]{49})$$

Автомобиль, стартуя с места и двигаясь с постоянным ускорением, через 10 секунд достигает скорости 90 км/ч. Какое расстояние в метрах пройдет автомобиль за первые 8 секунд разгона? Скорость автомобиля V и пройденное расстояние S находятся по формулам $$V=V_{0}+at$$, $$S=V_{0}t+\frac{at^2}{2}$$ где $$V_{0}$$ ‐ начальная скорость, a ‐ ускорение, t ‐ время

В трех литрах воды размешали 5 чайных ложек минерального удобрения, а в десяти литрах – две. Оба раствора слили в один бак и получили раствор удобрения нужной концентрации. Сколько чайных ложек удобрения нужно размешать в 65 литрах воды для получения раствора удобрения такой же концентрации?

Найдите наибольшее значение функции $$f(x)=(\frac{1}{2})^{\log_{\frac{1}{3}}(23-x^2+4x)}$$

В основании четырехугольной пирамиды SABCD лежит квадрат со стороной $$3\sqrt{2}$$. Ребро SA перпендикулярно плоскости основания и равно 8. Через вершину А параллельно BD проведено сечение, которое делит ребро SC в отношении 3:2, считая от вершины.

Окружность, вписанная в треугольник АВС, касается сторон ВА и ВС в точках Е и F.

Клиент планирует положить определенную сумму денег в банки под некоторые проценты. $$\frac{1}{3}$$ этой суммы он помещает на вклад А под r % процентов годовых, а оставшуюся часть денег на вклад Б под годовых (про начисляются в конце года и добавляются к сумме вклада). Через год сумма вклада (с учетом процентов) увеличилась на $$\frac{2}{15}$$ от первоначального значения, а через два года стала составлять 463 200 рублей. Если бы клиент изначально положил бы $$\frac{1}{3}$$ суммы вклада на вклад Б, а оставшиеся средства – на вклад А, то через год сумма вкладов (с учетом добавленных процентов) увеличилась бы на $$\frac{1}{6}$$ от первоначальной. Чему в этом случае была бы равна сумма вкладов через два года?

Найдите все значения параметра а, при каждом из которых система неравенств $$\left\{\begin{matrix} (a-x^{2})(a+x-2)<0\\x^{2}\leq 1 \end{matrix}\right.$$ не имеет решений

В течение дня посетители приходили к кассиру, желая произвести различные платежи (сумма любого платежа – четное число рублей). Каждый протягивал купюру номиналом 5000 рублей. Кассир выдавал сдачу, имея только 300 монет по 10 рублей и 500 монет по 2 рубля. По итогам дня все монеты оказались потраченными на сдачу.