362 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$79−x−\sqrt{x+11}=0$$
$$\sqrt{x+11}=79−x$$
ОДЗ: $$x<79$$
Возводим в квадрат
$$x+11=(79−x)^2$$
$$x^2−159x+6230=0$$
$$x=89$$ – не подходит под ОДЗ
$$x=70$$
Задание 2
Всего трехзначных чисел $$900$$
Из них на $$34$$ делятся $$102, 136, 170, 204,…,986 (=34\cdot3, 34\cdot4, 34\cdot5,…)$$ – всего их $$27$$ штук $$([900/34]=27)$$
$$P(A)=\frac{27}{900}\approx0,03$$
Задание 3
Пусть $$y$$ – неизвестная сторона
Одно из свойств описанного четырехугольника это суммы противоположных сторон равны друг другу
$$4x+9x=7x+y$$
$$6x=y$$
$$x=\frac{y}{6}$$
$$P=4x+7x+9x+y=338$$
$$20x+y=338$$
$$20x+6x=338$$
$$x=13$$
Большая сторона $$9x=117$$
Задание 4
$$\sin555°=\sin(180°\cdot3+15°)=−\sin15°$$
$$\sin1185°=\sin(180°\cdot6+105°)=\sin105°=\sin(90°+15°)=\cos15°$$
$$\tg405°=\tg(360°+45°)=\tg45°$$
$$−\sin15°\cdot\cos15°\cdot\tg45°=−0,5\sin30°\cdot1=−0,25$$
Задание 5
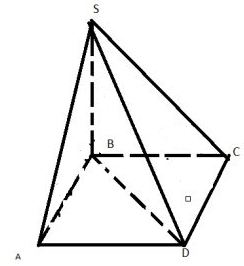
$$SB⟂(ABCD)$$
$$BC$$ – проекция $$SC$$ на $$ABCD$$
$$BC⟂DC$$ (т.к прямоугольник)
Значит по теореме о 3-х перпендикулярах $$SC⟂DC$$, значит $$∠BCS$$ – есть линейный угол двугранного угла $$∠SBCD$$
Аналогично с $$∠ABS$$
Пусть $$∠BCS=45$$ и $$∠ABS=30$$
$$△SBC$$ – прямоугольный и р/б значит $$BC=SB=4$$
$$AB=\frac{SB}{\tg30}=4\sqrt{3}$$
$$BD=\sqrt{AB^2+BC^2}=8$$
Задание 6
Если две прямые параллельные, то их угловые коэффициенты равны.
По геометрическому смыслу производной $$\tgα=k$$
$$\tgα=\tg(180−β)=−\tgβ$$
$$\tgβ=\frac{5}{4}=1,25\Rightarrow -1,25$$
Задание 7
$$\frac{2\cdot1200\cdot300}{t^2}\geq1800$$
$$t^2\leq400$$
$$−20\leq t\leq 20$$
Наибольшее время $$t=20$$
Задание 8
Из условия понятно, что задача на арифметическую прогрессию.
$$d=10$$
$$S_{10}=\frac{2a_1+10\cdot9}{2}\cdot10=700$$
$$a_1=25$$
$$S_{14}=\frac{2\cdot25+10\cdot13}{2}\cdot14=1260$$
$$S_{14}−S_{10}=560$$
Задание 9
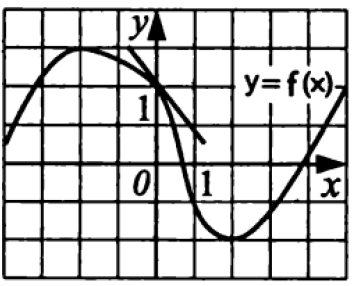
Из рисунка видно, какие точки удобнее всего взять
$$1=a^2+b$$
$$5=a^3+b$$
Вычтем одно из другого
$$a^3−a^2=4$$
$$a(a^2−a)=4$$, очевидно, что $$a=2$$
Значит, $$b=3$$
$$f(x)=2^x−3$$
$$f(6)=61$$
Задание 10
События:
$$A_1$$ - достанет стальной гвоздь и он не согнется
$$A_2$$ - достанет медный гвоздь и он не согнется
Они несовместные, значит
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)$$
$$P(A_1)=\frac{6}{10}\cdot0,9=0,54$$
$$P(A_2)=\frac{4}{10}\cdot0,7=0,28$$
$$P(A)=0,54+0,28=0,82$$
Задание 11
Найдём критические точки $$y'=0$$
$$\frac{3}{π}\cdot\cos x−\frac{3x−π}{π}\cdot\sin x−\frac{3}{π}\cos x=0$$
$$−\frac{3x−π}{π}\cdot\sin x=0$$
$$\sin x=0x=πn$$
$$x=\frac{π}{3}$$
Так как отрезок $$[0;2\pi]$$, то подозрительные точки:
$$x=0,\frac{π}{3},π,2π$$
Проверяем все.
$$y(2π)=26$$