267 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Задание 1
Зарплата жены составляет 40% дохода семьи из двух человек. На сколько процентов изменился доход семью после того, как зарплату мужа увеличили на 10%?
Зарплата мужа составит 60% от дохода семьи. Пусть доход x рублей, тогда у мужа была 0,6х рублей. После увеличения на 10% стала 0,6 x*1,1=0,66x и общий доход стал 0,4x+0,66x=1,06x, что составляет $$\frac{1,06x}{x}*100=106$$% , следовательно, увеличился на 6% .
Задание 2
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 400 км/ч?
При скорости 400 м\с подъемная сила составит 4 т.с.
Задание 3
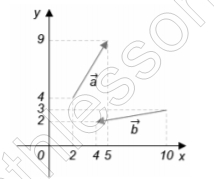
Зададим координаты векторов : $$\bar{a}(5-2;9-4)\Rightarrow$$ $$\bar{a}(3;5)$$; $$\bar{b} (4-10;2-3)\Rightarrow$$ $$\bar{b}(-6;-1)$$
Тогда координаты $$\bar{c} (3+(-6);5+(-1))\Rightarrow$$ $$\bar{c}(-3;4)$$
Следовательно, длина $$\left \| \bar{c} \right \|=\sqrt{(-3)^{2}+4^{2}}=5$$
Задание 4
Некоторый прибор состоит из трёх блоков. Если в работе одного из блоков происходит сбой, прибор отключается. Вероятность сбоя в течение года для первого и второго блоков составляет по 0,2, а для третьего блока – 0,1. Какова вероятность, что в течение года произойдёт хотя бы одно отключение данного прибора?
Вероятность стабильной работы для 1-го и 2-го составляет 1-0,2=0,8, для третьего 1-0,1=0,9. Тогда вероятность , что прибор ни разу не отключится : P=0,8*0,8*0,9=0,576 $$\Rightarrow$$ что хоть раз отключится 1-0,576=0,424
Задание 5
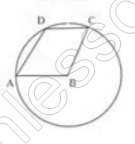
В трапеции АВСD (АВ||СD) угол DCB равен 72о. Окружность с центром в точке В проходит через точки А, D и С. Найдите величину угла ADC. Ответ дайте в градусах.
1) $$\angle ABC=180-\angle DCB=108$$ (по свойству трапеции) $$\Rightarrow$$ $$\smile ADC=\angle ABC=108$$ (по свойству центрального угла )
2) $$\smile AC$$ (большая ) $$=360-108=252$$$$\Rightarrow$$ $$\angle ADC=\frac{\smile AC}{2}=126$$( по свойству вписанного угла )
Задание 6
Функция у = f (x) определена на отрезке [‐3; 5]. На рисунке дан график её производной. Найдите количество точек минимума функции у = f (x).
Точка минимума на графике производной это точка, где производная равна нулю и график производной убывает $$\Rightarrow$$ есть на (-3; -2) и на $$(2; 3)\Rightarrow$$ 2 точки
Задание 7
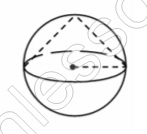
В шар вписан конус так, что центр основания конуса совпадает с центром шара. Найдите объем конуса, если объем шара равен 120.
Объем шара $$V=\frac{4}{3} \pi R^{3}=120$$
При этом объем конуса: $$V_{1}=\frac{1}{3}Sh$$, где $$S=\pi R^{2}$$ и $$h=R\Rightarrow$$ $$V_{1}=\frac{1}{3} \pi R^{3}=\frac{V}{4}=30$$
Задание 8
Найдите значение выражения $$3^{\sqrt{8}+10}\cdot 9^{-4-\sqrt{2}}$$
$$3^{\sqrt{8}+10}*9^{-4-\sqrt{2}}=$$$$3^{\sqrt{8}+10}*(3^{2})^{-4-\sqrt{2}}=$$$$3^{\sqrt{8}+10}*3^{-8-2\sqrt{2}}=$$$$3^{2\sqrt{2}+10-8-2\sqrt{2}}=3^{2}=9$$
Задание 9
Перед отправкой тепловоз издал гудок с частотой f0=190 Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из‐за эффекта Доплера частота второго гудка больше первого: она зависит от скорости тепловоза по закону $$f(v)=\frac{f_{0}}{1-\frac{v}{c}}$$ , где —скорость звука в воздухе (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы (считайте, что = 300 м/с). Ответ выразите в м/с.
Частота второго больше на 10 $$\Rightarrow$$ 200 Гц. Тогда : $$200=\frac{190}{1-\frac{v}{300}}\Leftrightarrow$$ $$200-\frac{2v}{3}=190\Leftrightarrow$$ $$\frac{2v}{3}=10\Leftrightarrow$$ $$2v=30$$ $$\Leftrightarrow$$ $$v=15$$
Задание 10
Сколько литров воды необходимо добавить к 0,5л 96%‐го раствора спирта, чтобы получить 40%‐й раствор спирта?
Количество спирта в 96% растворе:
$$x=\frac{0,5*96}{100}=0,48$$ л.
При этом это количество составляет 40%
$$y=\frac{0,48*100}{40}=1,2$$ л
Следовательно, необходимо добавить 1,2-0,5=0,7 л. воды
Задание 11
Найдите точку минимума функции $$y=x^{3}\cdot e^{x}$$
Найдем производную данной функции и приравняем к 0 : $$y^{'}=(x^{3})^{'}e^{x}+(e^{x})^{'}x^{3}=0\Leftrightarrow$$ $$3x^{2}e^{x}+e^{x}x^{3}=0\Leftrightarrow$$ $$x^{2}e^{x}(3+x)=0\Rightarrow$$ $$\left\{\begin{matrix}x=0\\x=-3\end{matrix}\right.$$
x=-3 точка минимума
Задание 12
A) ОДЗ: $$\left\{\begin{matrix}tg (x+\frac{\pi}{6})\neq 0\\\sin x\neq 0\\\cos (x+\frac{\pi}{6})\neq 0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}x+\frac{\pi}{6}\neq \pi n , n \in Z\\x\neq \pi k, k \in Z\\x+\frac{\pi}{6}\neq \frac{\pi}{2}+\pi m, m \in Z\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\neq -\frac{\pi}{6}\\x\neq \pi k\\x\neq \frac{\pi}{3}+\pi m, n,k,m \in Z\end{matrix}\right.$$
Решение: $$ctg \frac{110}{6}=-\sqrt{3}$$; $$tg(x+\frac{\pi}{6})=\frac{\sin (x+\frac{\pi}{6})}{\cos (x+\frac{\pi}{6})}=$$$$\frac{\frac{\sqrt{3}}{2}\sin x +\frac{1}{2} \cos x}{\frac{\sqrt{3}}{2} \cos x -\frac{1}{2} \sin x}=$$$$\frac{\sqrt{3} \sin x+\cos x}{\sqrt{3} \cos x-\sin x}$$; $$ctg x=\frac{\cos x}{\sin x}$$;
Получим $$-\sqrt{3} (\frac{\sqrt{3} \sin x+\cos x}{\sqrt{3} \cos x -\sin x})=$$$$\frac{2 \cos x}{\sin x}+3\Leftrightarrow$$ $$\frac{-3 \sin x -\sqrt{3} \cos x}{\sqrt{3} \cos x-\sin x}=$$$$\frac{2 \cos x+3 \sin x}{\sin x}\Leftrightarrow$$ $$-3\sin ^{2}x-\sqrt{3} \sin x\cos x=$$$$2\sqrt{3}\cos ^{2}x+3\sqrt{3} \cos x \sin x-2 \sin x \cos x-3 \sin ^{2}x\Leftrightarrow$$ $$2\sqrt{3} \cos ^{2}x+4\sqrt{3} \sin x \cos x-2 \sin x \cos x=0\Leftrightarrow$$ $$2 \cos x(\sqrt{3} \cos x+\sin x(2\sqrt{3}-1))=0\Leftrightarrow$$ $$\left[\begin{matrix}\cos x=0\\\sin x (2\sqrt{3} -1)+\sqrt{3} \cos x=0\end{matrix}\right.\Leftrightarrow$$$$\left[\begin{matrix}x=\frac{\pi}{2} +\pi n\\tg x=\frac{-3}{2\sqrt{3}-1}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\frac{\pi}{2}+ \pi n\\x=-arctg \frac{\sqrt{3}}{2\sqrt{3}-1}+ \pi k , n,k \in Z\end{matrix}\right.$$
Б) С учетом тригонометрической окружности : $$\frac{\pi}{2} +\pi n$$ :$$-\frac{3 \pi}{2}$$; $$-\frac{\pi}{2}$$ ;$$\frac{\pi}{2}$$; $$\frac{3 \pi}{2}$$
$$-arctg \frac{\sqrt{3}}{2\sqrt{3}-1}+\pi k$$: $$-\pi-arctg \frac{\sqrt{3}}{2\sqrt{3}-1}$$;$$-arctg \frac{\sqrt{3}}{2\sqrt{3}-1};$$ $$\pi-arctg \frac{\sqrt{3}}{2\sqrt{3}-1}$$.
Задание 13
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=4, AD=6, AA1=8 . Точка К, лежащая на ребре АА1, удалена от вершины А на 4, расстояние от точки L, лежащей на ребре DD1 до вершины D равно 2. Точка М лежит на отрезке В1С, длина МС вдвое больше длины В1М.
A) 1) K и L лежат в одной плоскости $$\Rightarrow$$ соединяем .
2) $$(ADD_{1}) \left | \right |(BCC_{1})\Rightarrow$$ через M пройдет прямая , параллельная KL . Пусть она пересекает $$BB_{1}$$ , в N и $$CC_{1}$$ в R $$\Rightarrow$$ (KNRL)-искомое сечение.
3) Зададим уравнение (KNRL) : введем ортогональную систему координат, тогда: $$K(0;0;4)$$; $$L(6; 0; 2)$$; $$M(\frac{1}{3} AD; AB ; \frac{2}{3} BB_{1})$$$$\Rightarrow$$ $$M(2 ;4; \frac{16}{3})$$
Пусть $$ax+by+cz+d=0$$ - уравнение (KNRL), тогда: $$\left\{\begin{matrix}a*0+b*0+c*4+d=0\\a*6+b*0+c*2+d=0\\a*2+b*4+c*\frac{16}{3}+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}4c+d=0\\6a+2c+d=0\\2a+4b+\frac{16c}{3}+d=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}c=-\frac{d}{4}\\a=-\frac{d}{12}\\b=\frac{d}{8}\end{matrix}\right.$$
Получим : $$-\frac{d}{12}x+\frac{d}{8}y-\frac{d}{4}z+d=0$$$$\Leftrightarrow$$ $$2x-3y+6z-24=0$$. Следовательно, нормаль-вектор для (KNRL) : $$\bar{n}(2; -3; 6)$$ . Для ($$DCC_{1}$$) : $$\bar{AD}$$ или $$\bar{Ox}(1 ;0;0)$$
$$\cos (\bar{n};\bar{Ox})=\cos ((KNRL);(DCC_{1}))=$$$$\frac{\left | 2*1+(-3)*0+6*0 \right |}{\sqrt{2^{2}+(-3)^{2}+6^{2}}\sqrt{1^{2}+0^{2}+0^{2}}}=$$$$\frac{2}{7}\Rightarrow$$ угол между этими плоскостями $$\alpha =arccos \frac{2}{7}$$
Б) 1) Пусть S - площадь (KLM), $$S_{1}$$ - площадь ее проекции на (ABC)-это и будет ABCD. Найдем $$\cos ((KLM ); (ABC))$$: нормаль вектора для (ABC) - $$\vec{Oz}(0;0;1)$$, тогда $$\cos ((KLM) ;(ABC))=\cos (\vec{n}; \vec{Oz})=$$$$\frac{\left | 2*0+(-3)*0+6*1 \right |}{\sqrt{2^{2}+(-3)^{2}+6^{2}}\sqrt{1^{2}}}=$$$$\frac{6}{7}=\cos \beta$$
2) $$S=\frac{S_{1}}{\cos \beta }=$$$$\frac{AB*AD}{\cos \beta }=$$$$\frac{6*4}{\frac{6}{7}}=28$$
Задание 14
Решите неравенство $$\frac{1}{2}\log_{x-1}(x^{2}-8x+16)+\log_{4-x} (-x^{2}+5x-4)>3$$
ОДЗ: $$\left\{\begin{matrix}x^{2}-8x+16>0\\x-1>0\\x-1\neq 1\\-x^{2}+5x-4>0\\4-x>0\\4-x\neq 1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}(x-4)^{2}>0\\x>1\\x\neq 2\\x>1\\x<4\\x\neq 3\end{matrix}\right.\Leftrightarrow$$ $$x \in (1;2)\cup (2;3) \cup (3;4)$$
Решение: $$\frac{1}{2} \log_{x-1}(x-4)^{2}+\log_{(4-x)}(-(x-1)(x-4))>3$$ $$\Leftrightarrow$$$$\frac{1}{2} *2 \log_{x-1}\left | x-4 \right |+\log_{4-x}(4-x)+\log_{4-x}(x-1)>3$$$$\Leftrightarrow$$ С учетом , что $$x<4$$ : $$\left | x-4 \right |=4-x$$ . Тогда: $$\log_{x-1}(4-x) +1+\log_{4-x} (x-1)-3>0\Leftrightarrow$$ $$\log_{x-1}(4-x)+\frac{1}{\log_{x-1}(4-x)}-2>0$$
Пусть $$\log_{x-1}(4-x)=y$$, тогда : $$y+\frac{1}{y}>0\Leftrightarrow$$ $$\frac{y^{2}-2y+1}{y}>0\Leftrightarrow$$ $$\frac{(y-1)^{2}}{y}>0\Leftrightarrow$$ $$\left\{\begin{matrix}y>0\\y-1\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\log_{x-1}(4-x)>0\\\log_{x-1}(4-x) \neq 1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>2\\x<3\\x\neq 2,5\end{matrix}\right.$$
С учетом ОДЗ: $$x \in (2 ;2,5)\cup (2,5; 3)$$
Задание 15
Площадь трапеции ABCD равна 6. Пусть Е – точка пересечения продолжений боковых сторон этой трапеции. Через точку Е и точку пересечения диагоналей трапеции проведена прямая, которая пересекает меньшее основание ВС в точке Р, а большее основание AD – в точке Q. Точка F лежит на отрезке ЕС, причем EF:FC=EP:EQ=1:3.
A) 1) Пусть P и Q не середины . $$\Delta PMC\sim \Delta AMQ$$$$\Rightarrow$$ $$\frac{PC}{AQ}=\frac{PM}{MQ}(1)$$
$$\Delta BPM\sim \Delta MQD\Rightarrow$$$$\frac{BP}{QD}=\frac{PM}{MQ}(2)$$
$$\Delta EPC\sim \Delta EQD\Rightarrow$$$$\frac{PC}{QD}=\frac{EP}{EQ}(3)$$
$$\Delta EBP\sim \Delta EAQ\Rightarrow$$$$\frac{BP}{AQ}=\frac{EP}{EQ}(4)$$
2) из (1) и (2) : $$\frac{PC}{AQ}=\frac{BP}{QD}(*)$$; Из (3) и (4) : $$\frac{PC}{QD}=\frac{BP}{AQ}(**)$$
Поделим (*) на (**): $$\frac{QD}{AQ}=\frac{AQ}{QD}\Rightarrow$$ $$QD=AQ\Rightarrow BP=PC$$
Б) 1) т.к. BP=PC и AQ=QD, то $$S_{BPQA}=S_{PCDQ}=\frac{S_{ABCD}}{2}=3$$
2) $$\frac{S_{ECP}}{S_{EDQ}}=$$$$(\frac{EP}{EQ})^{2}=$$$$\frac{1}{9}\Rightarrow$$ $$S_{ECP}=\frac{1}{9} S_{EDQ}$$ $$\Rightarrow$$$$S_{PCDQ}=\frac{8}{9}*S_{EDQ}\Rightarrow$$$$S_{ECP}=\frac{1}{8} S_{PCDQ}=\frac{3}{8}$$
3) $$\frac{S_{EFP}}{S_{ECP}}=\frac{EF*EP}{EC*EP}=$$$$\frac{1}{4}\Rightarrow$$ $$S_{EFP}=\frac{1}{4}*\frac{3}{8}=\frac{3}{32}$$
Задание 16
На покупку тетрадей в клетку и в линейку можно потратить не более 140 руб. Тетрадь в клетку стоит 3 руб, тетрадь в линейку – 2 руб. При закупке число тетрадей в клетку не должно отличаться от числа тетрадей в линейку более, чем на 9. Необходимо закупить максимально возможное суммарное количество тетрадей, при этом тетрадей в линейку нужно закупить как можно меньше. Сколько тетрадей в клетку и сколько тетрадей в линейку можно закупить при указанных условиях?
Пусть куплено x тетрадей в клетку и y – в линейку , тогда: $$3x+2y\leq 140$$. Раз в линейку как можно меньше, то и считается количество не более, чем на 9, то $$\left | x-y \right |\leq 9$$. При этом $$y\rightarrow min$$ и $$x+y\rightarrow max$$
Получим систему: $$\left\{\begin{matrix}3x+2y\leq 140\\\left | x-y \right |\leq 9\\x+y\rightarrow max\\y\rightarrow min\end{matrix}\right.$$$$\Leftrightarrow$$ $$\left\{\begin{matrix}y\leq 70-\frac{3x}{2}\\\left | x-y \right |\leq 9\\x+y\rightarrow max\\y\rightarrow min\end{matrix}\right.$$
Так как $$x,y \in N$$ и $$x+y\rightarrow max$$ , то $$\frac{3x}{2} \in N$$ и x – число четное .
Рассмотрим графическое решение:
Видим, что целые значения (26;31) ; (28;28) и (30;25) , в сумме дают 57;56 и 55 соответственно $$\Rightarrow$$ т .к. $$x+y\rightarrow max$$, то купим 26 в клетку и 31 линейку.
Задание 17
При каких значениях параметра a функция $$f(x)=4^{-x}+(\frac{1}{2})^{x+1}\cdot \frac{5a}{2}+\frac{a^{2}+12}{6}$$ принимает во всех точках отрезка [-1;1] значения больше 2.
Пусть $$2^{-x}=t>0\Rightarrow$$ $$4^{-x}=t^{2}$$. Получим $$(\frac{1}{2})^{x+1}=\frac{1}{2}*2^{-x}=\frac{t}{2}$$. При этом $$f(t)=t^{2}+\frac{5a}{4}t+\frac{a^{2}+12}{6}$$; $$x \in [-1 ;1]\Rightarrow$$ $$t \in [\frac{1}{2} ;2]$$
Рассмотрим систему: $$\left\{\begin{matrix}t^{2}+\frac{5a}{4}t+\frac{a^{2}+12}{6}>2\\t \in [\frac{1}{2}; 2]\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}t^{2}+\frac{5a}{4}t+\frac{a^{2}}{6}>0(1)\\t \in [\frac{1}{2}; 2]\end{matrix}\right.$$
Рассмотрим (1) : пусть $$g(t)=t^{2}+\frac{5a}{4}t+\frac{a^{2}}{6}$$, тогда $$g(t)>0$$ при $$t \in [\frac{1}{2} ;2]$$. Есть три случая .
1) Вершина $$g(t) \in [\frac{1}{2}; 2]$$, тогда для $$g(t)>0$$ на $$[\frac{1}{2}; 2]$$ необходимо, чтобы $$g(t_{0})>0$$: $$t_{0}=\frac{-\frac{5a}{4}}{2}=-\frac{5a}{8}\Rightarrow$$ $$g(t_{0})=(-\frac{5a}{4})^{2}+\frac{5a}{4}(-\frac{5a}{8})+\frac{a^{2}}{6}=$$$$-\frac{25a^{2}}{64}+\frac{a^{2}}{6}$$
При любом а $$g(t_{0})<0\Rightarrow$$ не подходит
2) $$t_{0}\leq \frac{1}{2} \Rightarrow$$ $$g(\frac{1}{2})>0$$ $$\Rightarrow$$ $$\left\{\begin{matrix}-\frac{5a}{8}\leq \frac{1}{2}\\(\frac{1}{2})^{2}+\frac{5a}{4}*\frac{1}{2}+\frac{a^{2}}{6}>0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}a\geq -\frac{4}{5}\\4a^{2}+15a+6>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a\geq -\frac{4}{5}\\\left[\begin{matrix}a<\frac{-15-\sqrt{129}}{8}\\a>\frac{-15+\sqrt{129}}{8}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$a>\frac{-15+\sqrt{129}}{8}$$
3) $$t_{0}\geq 2\Rightarrow$$ $$g(2)>0\Rightarrow$$ $$\left\{\begin{matrix}-\frac{5a}{8}\geq 2\\4+\frac{5a}{2}+\frac{a^{2}}{6}>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}a\leq -\frac{16}{5}\\\left[\begin{matrix}a<\frac{-15-\sqrt{129}}{2}\\a>\frac{-15+\sqrt{129}}{2}\end{matrix}\right.\end{matrix}\right.\Rightarrow$$ $$a<\frac{-15-\sqrt{129}}{2}$$
Тогда $$a \in (-\infty ;\frac{-15-\sqrt{129}}{2})\cup (\frac{-15+\sqrt{129}}{2}; +\infty )$$
Задание 18
Для членов последовательности a1,a2,...,a10 целых чисел при всех натуральных $$k\leq 8$$ выполняется неравенство ak+ak+2>2ak+1
A) т.к. $$a_{k}+a_{k+2}>2a_{k+1}\Leftrightarrow$$ $$a_{k}-a_{k+1}>a_{k+1}-a_{k}(*)$$ Пусть $$a_{10}=0$$, рассмотрим убывающую последовательность . Т.к. все числа целые и с учетом (*) получаем , что разность смежных меняется на 1. Например: $$a_{10}=0; a_{9}=1$$$$\Rightarrow$$ $$a_{9}-a_{10}=1$$$$\Rightarrow$$ $$a_{8}-a_{9}=2$$; $$min (a_{7} -a_{8})=3$$ и т.д. Получим : 45;36;28;21;15;10;6;3;1;0 , следовательно , может.
Б) Пусть разница между 1-ым и 2-м членами последовательности равна $$x_{1}$$, между 2-ым и 3-ым - $$x_{2}$$ и т .д. С учетом (*) получим $$x_{1}>+x_{2}...>x_{9}(**)$$ При этом $$x_{1}, ,,, x_{9}\in Z$$. Выразим $$a_{1}$$ и $$a_{7}$$ через $$a_{10}$$ и разницы ($$x_{1}...x_{9}$$):
$$a_{1}=a_{10}+(x_{1}+x_{2}+..+x_{9})=a_{10}+\sum_{i=1}^{9} x_{i}$$
$$a_{7}=a_{10}+(x_{9}+x_{8}+x_{7})=a_{10}+\sum_{i=7}^{9} x_{i}$$
Тогда $$a_{10}+\sum_{i=1}^{9} x_{i}+a_{10}=2(a_{10}+\sum_{i=1}^{9})\Leftrightarrow$$ $$x_{1}+x_{2}+..+x_{6}=x_{7}+x_{8}+x_{9}$$
С учетом (**) : $$x_{1}+x_{2}+..+x_{6}>x_{7}+x_{8}+x_{9}\Rightarrow$$ не может быть
B) Аналогично (Б) представим все через разности и $$a_{10}$$:
$$a_{1}=a_{10}+\sum_{i=1}^{9} x_{i}$$; $$a_{5}=a_{10}+\sum_{i=5}^{9} x_{i}$$; $$a_{6}=a_{10}+\sum_{i=6}^{9} x_{i}$$.
Тогда получим : $$a_{10}+\sum_{i=1}^{9} x_{i}-a_{10}+\sum_{i=5}^{9}x_{i}-a_{10}+\sum_{i=6}^{9} x_{i}-a_{10}=$$$$x_{1}+x_{2}+x_{3}+x_{4}-(x_{6}+x_{7}+x_{8}+x_{9})$$
Необходима минимальная разность между членами $$\Rightarrow$$ $$x_{8}=x_{9}+1$$; $$x_{7}=x_{8}+1=x_{9}+2$$ и $$x_{1}=x_{9}+8$$
Тогда получим : $$x_{9}+8+x_{9}+7+x_{9}+6+x_{9}+5-(x_{9}+3+x_{9}+2+x_{9}+1+x_{9})=$$$$5*4=20$$