255 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 255 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №255 (alexlarin.com)
Решаем ЕГЭ 255 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №255 (alexlarin.com)
Задание 1
Поезд Новосибирск‐Красноярск отправляется в 15:20 а прибывает в 4:20 на следующий день (время московское). Сколько часов поезд находится в пути?
До полуночи 8 часов 40 минут, после полуночи 4 часов 20 минут $$\Rightarrow$$ в сумме 13 часов
Задание 4
Во время психологического теста психолог предлагает каждому из двух испытуемых А. и Б. выбрать одну из трех цифр: 1, 2 или 3. Считая, что все комбинации равновозможны, найдите вероятность того, что А. и Б. выбрали разные цифры. Результат округлите до сотых
Всего возможных комбинаций: 9 - (11;12;13;21;22;23;31;32;33) Разные цифры в 6 комбинациях $$P=\frac{6}{9}=0,(6)\approx 0,67$$
Задание 7
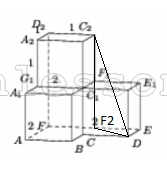
Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
$$DC^{2}_{2}=$$$$C_{2}F^{2}_{2}+DF_{2}^{2}=$$$$C_{2}F_{2}^{2}+DE^{2}+EF^{2}_{2}=$$$$2^{2}+1^{2}+1^{2}=6$$
Задание 8
Найдите значение выражения $$7\cos (\pi+\beta)-2\sin (\frac{\pi}{2}+\beta)$$, если $$\cos \beta=-\frac{1}{3}$$
$$7 \cos (\pi +B)-2\sin (\frac{\pi}{2}+B)=$$$$-7\cos \beta -2\cos \beta =-9\cos\beta =-9*(-\frac{1}{3})=3$$
Задание 9
Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле $$P=\frac{4mg}{\pi D^{2}}$$ где m = 1200 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения g = 10 м/с2 , а $$\pi=3$$, определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах
Выразим D из формулы : $$P=\frac{4mg}{\pi D^{2}}\Leftrightarrow$$ P \pi D^{2}=4mg\Leftrightarrow$$ $$D=\sqrt{\frac{4mg}{p \pi}}(D>0)$$
$$D=\sqrt{\frac{4*1200*10}{400*3}}=$$$$\sqrt{\frac{4}{100}}=\frac{2}{10}=0,2$$
Задание 10
Игорь и Паша могут покрасить забор за 9 часов. Паша и Володя могут покрасить этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроём?
Пусть x - производительность Игоря, y - Паши, z - Володи(в частях забора в час) . Весь забор примем за 1.
$$\left\{\begin{matrix}\frac{1}{x+y}=9\\\frac{1}{y+z}=12\\\frac{1}{x+z}=18\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x+y=\frac{1}{9}\\y+z=\frac{1}{12}\\x+z=\frac{1}{18}\end{matrix}\right.$$
Сложим уравнения:
$$2(x+y+z)=\frac{1}{9}+\frac{1}{12}+\frac{1}{18}=\frac{9}{36}=\frac{1}{4}\Leftrightarrow$$ $$x+y+z=\frac{1}{8}\Leftrightarrow$$ $$\frac{1}{x+y+z}=8$$ часов
Задание 11
Найдите наибольшее значение функции $$y=\frac{x^{3}+x^{2}+9}{x}-x^{2}$$ на отрезке [-9;-1]
$$y=\frac{x^{3}+x^{2}+9}{x}-x^{2}=\frac{x^{3}+x^{2}+9-x^{3}}{x}=\frac{x^{2}+9}{x}$$
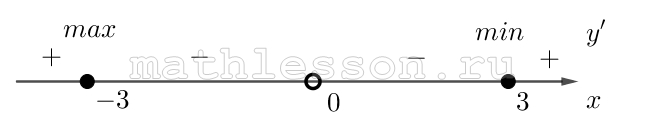
$${y}'=\frac{{(x^{2}+9)}'x-(x^{2}+9)*{x}'}{x^{2}}=\frac{2x^{2}-x^{2}-9}{x^{2}}=\frac{x^{2}-9}{x^{2}}=0$$
$$\left\{\begin{matrix}x^{2}-9=0\\x^{2}\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\pm 3\\x\neq 0\end{matrix}\right.$$
$$f(-3)=\frac{(-3)^{2}+9}{(-3)}=-6$$
Задание 12
A) $$\sqrt{10}\cos x-\sqrt{4 \cos x- \cos 2x}=0\Leftrightarrow$$$$\sqrt{4 \cos x-\cos 2x}=\sqrt{10}\cos x$$
Прейдем к равносильной системе:$$\left\{\begin{matrix}\sqrt{10} \cos x\geq 0(2)\\4 \cos x- \cos 2x =10 \cos ^{2}x (1)\end{matrix}\right.$$
Рассмотрим (1): $$4 \cos x-(2 \cos^{2}x-1)-10 \cos ^{2}x=0\Leftrightarrow$$$$-12 \cos ^{2}x+4 \cos x+1=0\Leftrightarrow$$$$12 \cos ^{2}x-4 \cos x-1=0$$
$$D=16+48=64=8^{2}$$
$$\left[\begin{matrix}\cos x=\frac{4+8}{24}=\frac{1}{2}\\\cos x=\frac{4-8}{24}=-\frac{1}{6}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}x=\pm \frac{\pi}{3}+2 \pi n , n \in Z\\ \varnothing (\cos x\geq 0)\end{matrix}\right.$$
Б) На промежутке $$[-\frac{\pi}{3};2 \pi n ]$$:
$$-\frac{\pi}{3}+2 \pi n:n=1\Rightarrow \frac{5 \pi}{3}$$
$$\frac{\pi}{3}+2 \pi n:n=0\Rightarrow \frac{\pi}{3}$$
Задание 13
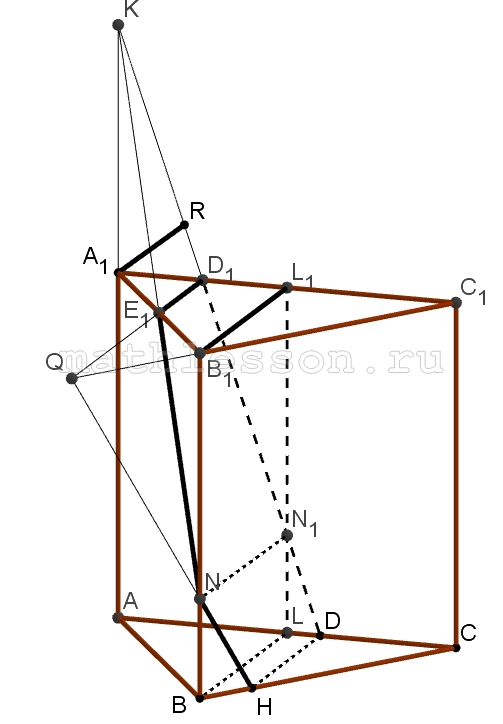
Основание прямой призмы ABCA1B1C1 равнобедренный треугольник ABC, в котором AB=BC=5, AC=6 . Высота призмы равна $$\sqrt{6}$$ . На сторонах A1C1, A1B1 и AC выбраны соответственно точки D1, E1 и D так, что , $$A_{1}D_{1}=\frac{A_{1}C_{1}}{4}$$, $$A_{1}E_{1}=B_{1}E_{1}$$, $$CD=\frac{AC}{3}$$, и через эти точки проведена плоскость.
А) 1) Соединим $$D_{1}E_{1}$$, т.к. $$(ABC) \left | \right |(A_{1}B_{1}C_{1})$$, то из D пойдет прямая DH ($$DH\cap BC=H$$) и $$D_{1}C_{1}\left | \right |DH$$
2) Пусть $$D_{1}E_{1}\cap C_{1}B_{1}=Q$$. Соединим $$QH\cap BB_{1}=N$$, соединим $$DD_{1}\Rightarrow$$ $$D_{1}D+NE_{1}$$ - искомое сечение
3) $$A_{1}D_{1}=D_{1}L_{1}$$($$B_{1}L_{1}$$ - высота ), $$A_{1}E_{1}=E_{1}B_{1}$$$$\Rightarrow$$ $$D_{1}E_{1}=\frac{1}{2}B_{1}L_{1}$$ и $$D_{1}E_{1}\left | \right |B_{1}L_{1}$$; $$B_{1}L_{1}=\sqrt{B_{1}C_{1}^{2}-L_{1}C_{1}^{2}}=4$$$$\Rightarrow$$ $$E_{1}D_{1}=2$$
4) $$DH\left | \right |D_{1}E_{1}\Rightarrow$$ $$DH\left | \right |BL$$ (BL - высота) $$\Rightarrow$$ $$\frac{DH}{LB}=\frac{CD}{CL}$$; $$CD=\frac{AC}{3}=2$$, $$CL=3\Rightarrow$$ $$DH=\frac{2*4}{3}=\frac{8}{3}$$
5) $$S_{D_{1}N_{1}NE_{1}}=\frac{D_{1}E_{1}*N_{1}N}{2}*DN_{1}$$; $$S_{NN_{1}DH}=\frac{DH*NN_{1}}{2}*DN_{1}$$ ($$AA_{1}\perp DH$$, $$AD\perp DH$$$$\Rightarrow$$ $$D_{1}D\perp DH$$); $$NK_{1}=BL=4;D_{1}B_{1}=\sqrt{D_{1}L_{1}^{2}+L_{1}N_{1}^{2}}$$$ $$D_{1}L=1,5 ; LD=1$$$$\Rightarrow$$ $$\frac{L_{1}N_{1}}{M_{1}L}=\frac{3}{2}$$ ($$\Delta D_{1}L_{1}N_{1}\sim \Delta N_{1}LD)$$$$\Rightarrow$$ $$L_{1}L=AA_{1}=\sqrt{6}=5x$$$$\Rightarrow$$ $$x=\frac{\sqrt{6}}{5}\Rightarrow$$ $$L_{1}N_{1}=\frac{3\sqrt{6}}{5}$$, $$N_{1}L=\frac{2\sqrt{6}}{5}$$)
$$D_{1}B_{1}=\sqrt{(\frac{3}{2})^{2}+(\frac{3\sqrt{6}}{5})^{2}}=\frac{21}{10}$$
$$D{1}D=\frac{7}{2}$$
$$DN_{1}=\sqrt{1^{2}+(\frac{2\sqrt{6}}{5})^{2}}=\frac{7}{5}$$
$$S_{D_{1}N_{1}NE_{1}}=\frac{2+4}{2}*\frac{21}{10}=\frac{63}{10}$$
$$S=\frac{63}{10}+\frac{14}{3}=\frac{329}{30}$$
$$S_{DHN_{1}N}=\frac{\frac{8}{3}+4}{2}*\frac{7}{5}=\frac{14}{3}$$
Б) 1) Пусть $$DD_{1}\cap AA_{1}=K$$ $$\Delta KD_{1}A_{1}\sim \Delta KAD$$; $$\frac{A_{1}D}{AD}=\frac{KD_{1}}{KD}=\frac{KA_{1}}{KA}=\frac{1,5}{4}=\frac{3}{8}$$. Пусть $$KA_{1}=x\Rightarrow$$ $$KA=x+\sqrt{6}\Rightarrow$$ $$\frac{x}{x+\sqrt{6}}=\frac{3}{8}\Leftrightarrow$$ $$8x=3x+3\sqrt{6}\Leftrightarrow$$ $$x=\frac{3\sqrt{6}}{5}$$. Пусть $$KD_{1}=y\Rightarrow$$ $$KD=y+\frac{7}{2}\Rightarrow$$ $$\frac{y}{y+\frac{7}{2}}=\frac{3}{8}\Rightarrow$$ $$y=\frac{21}{10}$$
2) Пусть $$A_{1}R\perp KD_{1}$$, но $$A_{1}D_{1}D_{1}E_{1}$$$$\Rightarrow$$ $$A_{1}R\perp D_{1}E_{1}$$ и $$A_{1}R\perp KD_{1}E_{1}$$.
$$A_{1}R=\frac{A_{1}K*A_{1}D_{1}}{KD_{1}}=$$$$\frac{\frac{3\sqrt{6}}{5}*\frac{3}{2}}{\frac{21}{10}}=$$$$\frac{9\sqrt{6}*10}{5*2*21}=\frac{3\sqrt{6}}{7}$$
Задание 14
Решите неравенство $$(\sqrt[3]{2})^{x^{2}+4x+1}-(\sqrt{3+\sqrt{8}}-1)^{x}\leq 0$$
$$(\sqrt[3]{2})^{x^{2}+4x+1}-(\sqrt{3+\sqrt{8}}-1)^{x}\leq 0$$
$$\sqrt{3+\sqrt{8}}=\sqrt{2+1+2\sqrt{2}}=\sqrt{(\sqrt{2}+1)^{2}}=\left | \sqrt{2}+1 \right |=\sqrt{2}+1$$
$$\sqrt[3]{2}^{x^{2}+4x+1}-(\sqrt{2}+1-1)^{x}\leq 0\Leftrightarrow$$ $$2^{\frac{x^{2}+4x+1}{3}}\leq 2^{\frac{x}{2}}\Leftrightarrow$$ $$\frac{x^{2}+4x+1}{3}\leq \frac{x}{2}|*6\Leftrightarrow$$ $$2x^{2}+8x+2\leq 3x\Leftrightarrow$$ $$2x^{2}+5x+2\leq 0$$
$$D=25-16=9$$
$$x_{1}=\frac{-5+3}{4}=-0,5$$
$$x_{2}=\frac{-5-3}{4}=-2$$
$$(x+0,5)(x+2)\leq 0$$
$$x \in [-2, -0,5]$$
Задание 15
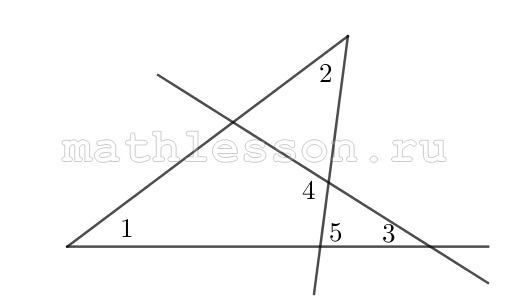
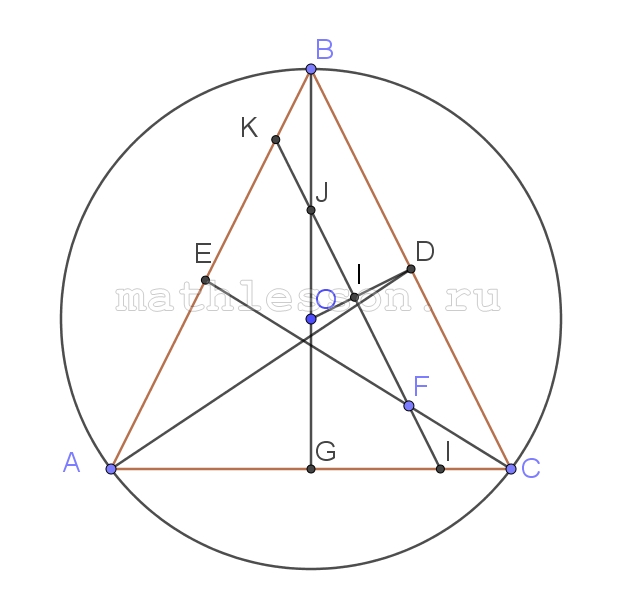
Дан треугольник АВС, в котором АВ=ВС=5, медиана $$AD=\frac{\sqrt{97}}{2}$$ . На биссектрисе СЕ выбрана точка F такая, что CE=5CF. Через точку F проведена прямая l, параллельная ВС.
А) 1) $$\Delta ABD$$: $$\cos B=\frac{AB^{2}+BD^{2}-AD^{2}}{2 AB*BD}=\frac{7}{25}$$
2) $$\Delta ABC:$$ $$AC=\sqrt{AB^{2}+BC^{2}-2 AB*BC * \cos B}=6$$
3) $$BG=\sqrt{BC^{2}-GC^{2}}=4\Rightarrow$$ $$S_{ABC}=\frac{1}{2}BG*AC=12$$
4) $$BO=\frac{AB*BC*AC}{4 S_{ABC}}=\frac{25}{8}$$
5) $$\cos BCA=\frac{GC}{BC}=\frac{3}{5}$$; $$\angle ECG=\frac{\angle BCA}{2}$$$$\Rightarrow$$ $$2 \cos ^{2}ECG-1=\frac{3}{5}$$$$\Rightarrow$$ $$\cos ECG=\frac{2}{\sqrt{5}}$$; $$\sin ECG=\frac{1}{\sqrt{5}}$$
$$CE=\frac{2 AC*CB*\cos ECG}{AC+CB}=\$$$$frac{120}{11\sqrt{5}}$$$$\Rightarrow$$ $$CF=\frac{CE}{5}=\frac{24}{11\sqrt{5}}$$
6) Центр описанной на пересечении серединных перпендикуляров , $$BD=DC\Rightarrow$$ $$OD\perp BC$$ и OH - расстояние
7) $$\angle FIG=\angle BCA\Rightarrow$$$$\sin FIG=\sin BCA=\frac{4}{5}$$
$$\angle FIG=180-\angle FIG\Rightarrow$$ $$\sin FIC=\sin FIG=\frac{4}{5}$$
$$\cos FIC=-\cos FIG=-\cos BSA=-\frac{3}{5}$$
По теореме синусов: $$\frac{FC}{\sin FIC}=\frac{FI}{\sin FCI}\Rightarrow$$$$FI=\frac{6}{11}$$
8) $$\Delta JGJ\sim \Delta BGC\Rightarrow$$ $$\frac{IC}{CG}=\frac{BJ}{BG}\Rightarrow$$ $$BJ=\frac{8}{11}\Rightarrow$$ $$JO=BO-BJ=\frac{211}{8*11}$$
9) $$\Delta BOD\sim \Delta BGC\Rightarrow$$ $$\frac{OD}{GC}=\frac{BO}{BC}\Rightarrow$$ $$OD=\frac{5}{18}$$
10) $$\Delta JOH\sim \Delta BOD\Rightarrow$$ $$\frac{JO}{BO}=\frac{OH}{OD}\Rightarrow$$ $$OH=\frac{633}{440}$$
Б) 1) $$\Delta ABC\sim \Delta AKI\Rightarrow$$ $$S_{AKI}=S_{ABC}(\frac{AI}{AC})^{2}$$
$$\frac{AI}{AC}=(\frac{6-\frac{6}{11}}{6})^{2}=\frac{100}{121}\Rightarrow$$ $$S_{AKI}=\frac{1200}{121}$$
2) $$S_{KBCI}=S_{ABC}-S_{AKI}=\frac{252}{121}\Rightarrow$$ $$\frac{S_{AKI}}{S_{KBCI}}=\frac{100}{21}$$
Задание 16
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
Известно, что в пятый месяц кредитования нужно выплатить 44 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Пусть S-сумма кредита в тыс. руб. , n=9-число месяцев, r=4%. Кредит на 9 месяцев, следовательно, по основной част долга ежемесячный платеж $$\frac{S}{9}$$ . Составим таблицу:
| Месяц | Долг на начало месяца | Начисленный процент | Итоговый платеж |
| 1 | S | $$\frac{rS}{100}$$ | $$\frac{S}{9}+\frac{rS}{100}$$ |
| 2 | $$S-\frac{S}{9}=\frac{8S}{9}$$ | $$\frac{r*8S}{100*9}$$ |
$$\frac{S}{9}+\frac{rS}{100}*\frac{8}{9}$$ |
| 3 | $$\frac{8S}{9}-\frac{S}{9}=\frac{7S}{9}$$ | $$\frac{rS}{100}*\frac{7}{9}$$ | $$\frac{S}{9}+\frac{rS}{100}*\frac{7}{9}$$ |
| ... | ... | ... | ... |
| 5 | $$\frac{6S}{9}-\frac{S}{9}=\frac{5S}{9}$$ | $$\frac{rS}{100}*\frac{5}{9}$$ | $$\frac{S}{9}+\frac{rS}{100}*\frac{5}{9}$$ |
| ... | ... | ... | ... |
| 9 | $$\frac{2S}{9}-\frac{S}{9}=\frac{S}{9}$$ | $$\frac{rS}{100}*\frac{1}{9}$$ | $$\frac{S}{9}+\frac{rS}{100}*\frac{1}{9}$$ |
Получим $$\frac{S}{9}+\frac{4*S*5}{100*9}=44\Leftrightarrow$$ $$5S+S=44*45\Leftrightarrow$$ $$6S=44*45\Leftrightarrow$$ $$S=330 $$тыс.руб.
Тогда итоговые выплаты составят: $$S+\frac{rS}{100}(1+\frac{8}{9}+\frac{7}{9}+...+\frac{1}{9})=1,2S=396$$ тыс. руб (сложили суммы с четвертого столбика)
Задание 17
При каких значениях параметра a система $$\left\{\begin{matrix}|x-a|+|y-a|+|a+1-x|+|a+1-y|=2\\ y+2|x-5|=6\end{matrix}\right.$$ имеет единственное решение
Пусть m=y-a; n=x-a, тогда имеем
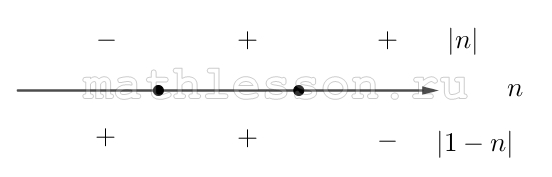
$$\left | m \right |+\left | 1-m \right |=2-\left | n \right |-\left | 1-n \right |(m(n))$$
Рассмотрим раскрытие модулей:
1) $$n\leq 0$$: $$2-\left | n \right |-\left | 1-n \right |=1+2n$$. Тогда $$m(n)$$: $$\left | m \right |+\left | 1-m \right |=1+2n$$. Раскроем модули:
a) $$m\leq 0$$: $$-2m+1=1+2n\Leftrightarrow$$ $$m=-n$$, с учетом, что $$n\leq 0$$ , то $$m=-n$$ при $$n=0$$ и $$m=0$$
b) $$m \in (0;1]$$: $$1=1+2n\Leftrightarrow$$ $$n=0$$
c) $$m \in (1;+\infty )$$: $$2m-1=1+2n\Leftrightarrow$$ $$m=n+1$$ при $$n\leq 0$$ – решений нет
2) $$0<n\leq 1$$:$$ 2-\left | n \right |-\left | 1-n \right |=1$$
a) $$m\leq 0$$: $$-2m+1=1\Leftrightarrow$$ $$m=0$$
b) $$0<m\leq 1$$: $$1=1\Rightarrow$$ решение все точки в квадрате
$$\left\{\begin{matrix}0<n\leq 1\\0<m\leq 1\end{matrix}\right.$$
c) $$m>0$$: $$2m-1=1\Rightarrow$$ $$m=1$$ решений нет
3) $$n>1$$: $$2-\left | m \right |-\left | 1-n \right |=3-2n$$
a) $$m\leq 0$$: $$-2m+1=3-2n\Leftrightarrow$$ $$m=n-1$$, с учетом , что $$n>1$$ решений нет
b) $$a<m\leq 1$$: $$1=3-2n\Rightarrow$$ $$n=1\Rightarrow$$ решений нет
c) $$m>1$$: $$2m-1=3-2n\Leftrightarrow$$ $$m=2-n$$ решений нет
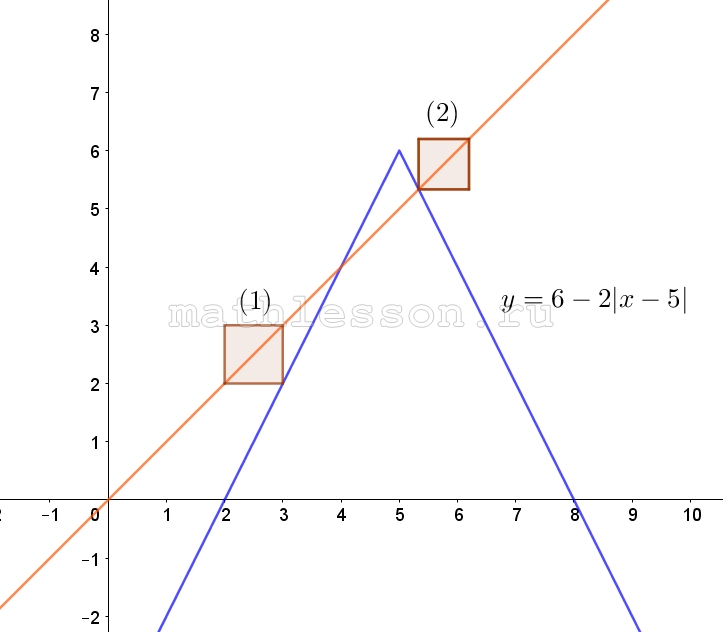
Построим график m(n). С учетом , что m=y-a и n=y-a , то график y(x) будет строиться смещение вершины (0;0) на (a;a) ( по прямой (y=x)), и построим график $$y=6-2\left | x-5 \right |$$ - cуществует 2 случая с одним решением :
1) При a=2
2) При пересечении вершиной и диагональю y=x части графика $$y=6-2\left | x-5 \right |$$(она задается y=16-2x)
$$\left\{\begin{matrix}y=x\\y=16-2x\end{matrix}\right.\Leftrightarrow$$ $$x=16-2x\Leftrightarrow$$ $$3x=16\Rightarrow$$ $$x=\frac{16}{3}\Rightarrow$$ $$a=\frac{16}{3}$$
Задание 18
В последовательности натуральных чисел a1=47 , каждый следующий член равен произведению суммы цифр предыдущего члена и a1
A) $$a_{2}=(4+7)*47=517$$
$$a_{3}=(5+1+7)*47=611$$
$$a_{4}=(6+1+1)*47=376$$
$$a_{5}=(3+7+6)*47=752$$
Б) вычислим еще несколько членов.
$$a_{6}=(7+5+2)*47=14*47=658$$
$$a_{7}=(6+5+8)*47=19*47=893$$
$$a_{8}=(8+9+3)*47=20*47=940$$
$$a_{9}=(9+4+0)*47=13*47=611=a_{3}$$
Получаем повторение с периодом: $$9-3=6 \Rightarrow$$ $$a_{50}=a_{8}=940$$ (можно составить таблицу, можно посчитать 50-2=48(т.к. начинаем с 3-го) и 48/6=8 полных повторений без остатка , следовательно $$a_{50}$$ равен крайнему в выборке $$a_{3}...a_{8}$$)
B) $$\sum_{8}^{n=3} a_{n}=61+376+752+..+940=4230$$
Тогда $$\sum_{n=3}^{5a}=4230*8=33840$$
С учетом $$a_{1}$$ и $$a_{2}$$, получим $$34404$$