231 вариант Алекса Ларина. Разбор ЕГЭ математика 2018.
Решаем ЕГЭ 231 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №231 (alexlarin.com)
Решаем ЕГЭ 231 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №231 (alexlarin.com)
Задание 1
Железнодорожный билет для взрослого стоит 290 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 16 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу?
Стоимость билета для школьника $$0,5\cdot290$$
Общая стоимость: $$16\cdot0,5\cdot290+3\cdot290=8\cdot290+3\cdot290=11\cdot290=3190$$
Задание 2
На диаграмме показано количество посетителей сайта РИА Новости в течение каждого часа 8 декабря 2009 года. По горизонтали указывается номер часа, по вертикали – количество посетителей сайта за данный час. Определите по диаграмме, сколько часов за эти сутки аудитория посетителей сайта РИА Новости находилась в пределах от 30 до 50 тыс.
Задание 4
В 10‐х классах 51 учащийся, среди них две подруги – Марина и Настя. Для написания ВПР по географии 10‐классников случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Марина и Настя окажутся в одной группе.
В каждой группе: $$\frac{51}{3}=17$$
Пусть Марина уже есть в группе, тогда в ней остается 16 свободных мест, а человек на них претендует 50: $$p=\frac{16}{50}=0,32$$
Задание 5
В равнобедренном треугольнике ABC с основанием AC боковая сторона равна $$4\sqrt{15}$$, $$\sin\angle BAC=0,25$$. Найдите длину высоты AH.
$$\cos BAC=\sqrt{1-\sin^{2}BAC}=\sqrt{1-\frac{1}{16}}=\frac{\sqrt{15}}{4}$$; $$BC^{2}=AB^{2}+AC^{2}-2AB\cdot AC\cdot\cos BAC$$ $$\Leftrightarrow$$ $$x^{2}-2\cdot4\sqrt{15}\cdot x\cdot\frac{\sqrt{15}}{4}=0$$; $$x^{2}-30x=0$$ $$\Rightarrow$$ $$x=30$$
из $$\bigtriangleup AHC$$: $$\frac{AH}{AC}=\sin\angle BCA$$ $$\Rightarrow$$ $$AH=AC\cdot\sin\angle BCA=30\cdot\frac{1}{4}=7,5$$
Задание 7
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
$$V=\frac{1}{3}S_{osn}\cdot h$$
Пусть а - сторона основания, тогда: $$S_{osn}=\frac{\sqrt{3}a^{2}}{4}\cdot6=\frac{3\sqrt{3}a^{2}}{2}$$; $$h=\frac{3V}{S_{osn}}=\frac{3\cdot6}{\frac{3\sqrt{3}\cdot1}{2}}=$$ $$\frac{3\cdot4}{\sqrt{3}}=4\sqrt{3}$$; $$SE=\sqrt{CH^{2}+HE^{2}}=\sqrt{48+1}=\sqrt{49}=7$$
Задание 8
Найти $$\cos4x$$, если $$\sin x-\cos x=\frac{3}{\sqrt{10}}$$
$$\sin^{2}x-2\sin x\cos x+\cos^{2}x=\frac{9}{10}$$
$$-\sin2x=-\frac{1}{10}$$; $$\sin2x=\frac{1}{10}$$; $$\cos4x=1-2\sin^{2}2x=1-2(\frac{1}{10})^{2}=1-\frac{2}{100}=0,98$$
Задание 9
Автомобиль, движущийся в начальный момент времени со скоростью $$v_{0}=30$$ м/с, начал торможение с постоянным ускорением а = 4 м/с 2. За t секунд после начала торможения он прошёл путь $$S=v_{0}t\frac{at^{2}}{2}$$(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 112 метров. Ответ выразите в секундах.
$$112=30t-\frac{4t^{2}}{2}$$; $$2t^{2}-30t+112=0$$; $$t^{2}-15t+56=0$$; $$\left\{\begin{matrix}t_{1}=7\\t_{2}=8\end{matrix}\right.$$
Задание 10
Расстояние между городами A и B равно 550 км. Из города A в город B со скоростью 50 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 75 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся? Ответ дайте в километрах.
Пусть х -время второго, тогда $$x+1$$ - время первого: $$50\cdot(x+1)+75x=550$$; $$125x+50=560$$; $$x=4$$; $$S=50\cdot(4+1)=250$$
Задание 11
Найдите наибольшее значение функции $$y=18\sin x-9\sqrt{3}+1,5\sqrt{3}\pi+21$$на отрезке $$[0;\frac{\pi}{2}]$$
$$y'=18\cos x-9\sqrt{3}-0$$; $$\cos x-\frac{\sqrt{3}}{2}=0$$; $$\left\{\begin{matrix}x=\frac{\pi}{6}+2\pi n,n\in Z\\x=\frac{5\pi}{6}+2\pi n,n\in Z\end{matrix}\right.$$;
$$y(\frac{\pi}{6})=18\sin\frac{\pi}{6}-9\sqrt{3}\frac{\pi}{6}+1,5\sqrt{3}\pi+21=18\cdot\frac{1}{2}+21=30$$
Задание 12
Дано уравнение $$\sqrt{\sin2x}=\sqrt[4]{2}\cdot\sqrt{\cos x}$$
a) ОДЗ: $$\left\{\begin{matrix}\sin2x\geq0\\\cos x\geq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}2\pi n\leq2x\leq\pi+2\pi n\\-\frac{\pi}{2}+2\pi n\leq x\leq\frac{\pi}{2}+2\pi n\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\pi n\leq x\leq\frac{\pi}{2}+\pi n\\-\frac{\pi}{2}+2\pi n\leq x\leq\frac{\pi}{2}+2\pi n\end{matrix}\right.$$
$$x\in[2\pi n;\frac{\pi}{2}+2\pi n]\cup{-\frac{\pi}{2}+2\pi n},n\in Z$$
$$\sin2x=\sqrt{2}\cos x$$; $$2\sin x\cos x-\sqrt{2}\cos x=0$$; $$\sqrt{2}\cos x(\sqrt{2}-1)=0$$; $$\left\{\begin{matrix}\cos x=0\\\sin x=\frac{\sqrt{2}}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\frac{\pi}{2}+\pi n\\x=(-1)^{n}\frac{\pi}{4}+\pi n,n\in Z\end{matrix}\right.$$
С учетом ОДЗ: $$\frac{\pi}{2}+2\pi n;\frac{\pi}{4}+2\pi n,n\in Z$$
б) $${-\frac{3\pi}{2};-\frac{\pi}{2}}$$
Задание 13
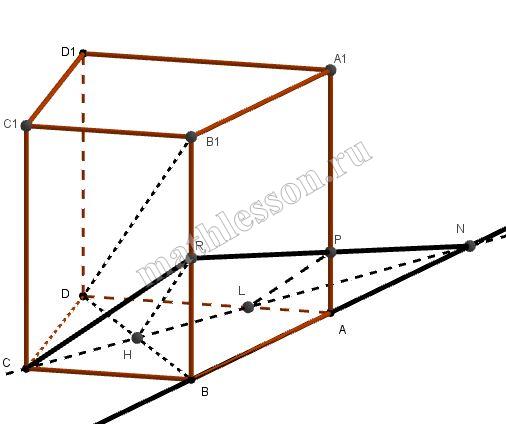
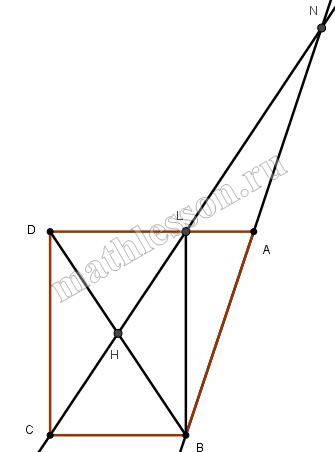
В основании прямой призмы $$ABCDA_{1}B_{1}C_{1}D_{1}$$ лежит прямоугольная трапеция АВСD с основаниями ВС и АD (ВС < АD), в которой АВ=5, CD=4, ВС=6. Через точку С и середину ребра $$BB_{1}$$ параллельно $$B_{1}D$$ проведена плоскость β.
Задание 14
Решите неравенство $$\frac{7\cdot4^{x}+2^{x^{2}+1}}{3-2^{2x-x^{2}}}\geq2^{2x+3}$$
$$\frac{7\cdot2^{2x}+\cdot2^{x^{2}}}{3-\frac{2^{2x}}{2^{x^{2}}}}\geq2^{2x}\cdot8$$
Пусть $$2^{2x}=a>0$$; $$2^{x^{2}}=b>0$$
$$\frac{7a+2b}{3-\frac{a}{b}}\geq8a$$; $$\frac{(7a+2b)b}{3b-a}\geq\frac{8a(3b-a)}{3b-a}$$; $$3\cdot2^{x^{2}}-2^{2x}=2^{\log_{2}3}\cdot2^{x^{2}}-2^{2x}=2^{x^{2}+\log_{2}3}-2^{2x}$$ $$\Rightarrow$$ всегда$$>0$$
$$x^{2}+\log_{2}3-2x=0$$
$$D=4-4\log_{2}3=\log_{2}16-\log_{2}81<0$$
$$7ab+2b^{2}\geq24ab-8a^{a}$$; $$2b^{2}-17ab+8a^{2}\geq0$$ $$|\div a^{2}$$;
$$2(\frac{b}{a})^{2}-17\frac{b}{a}+8\geq0$$
$$D=289-64=225$$;
$$\frac{b}{a}=\frac{17+15}{4}=8$$; $$\frac{b}{a}=\frac{17-15}{4}=\frac{1}{2}$$;
$$\left\{\begin{matrix}\frac{b}{a}\geq8\\\frac{b}{a}\leq\frac{1}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{2^{x^{2}}}{2^{2x}}\geq8\\\frac{2^{x^{2}}}{2^{2x}}\leq\frac{1}{2}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}2^{x^{2}-2x}\geq2^{3}\\2^{x^{2}-2x}\leq2^{-1}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}-2x\geq3\\x^{2}-2x\leq-1\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x^{2}-2x-3\geq0\\x^{2}-2x+1\leq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}(x-3)(x+1)\geq0\\(x-1)^{2}\leq0\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x\geq3\\x<-1\\x=1\end{matrix}\right.$$
Задание 15
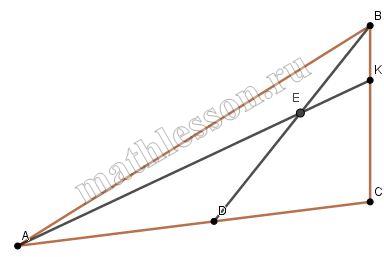
На стороне ВС треугольника АВС отмечена точка К. Оказалось, что отрезок АК пересекает медиану ВD в точке Е так, что АЕ=ВС.
а) 1) По т. Менелая: $$\frac{AE}{EK}\cdot\frac{BK}{BC}\cdot\frac{CD}{DA}=1$$; $$AE=BC$$; $$CD=DA$$ $$\Rightarrow$$ $$\frac{BK}{EK}\cdot\frac{1}{1}\cdot\frac{1}{1}=1$$ $$\Rightarrow$$ $$BK=EK$$
ч.т.д.
б) 1) Пусть $$BK=EK=x$$; $$AK=7+x$$; $$KC=7-x$$; $$AC=8$$
$$\bigtriangleup ABC$$: $$\cos C=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{64+49-169}{2\cdot8\cdot7}=-\frac{1}{2}$$ $$\Rightarrow$$ $$\angle C=120^{\circ}$$; $$\bigtriangleup AKC$$: $$AK^{2}=AC^{2}+KC^{2}-2AC\cdot KC\cdot\cos C$$ $$\Leftrightarrow$$ $$(7+x)^{2}=8^{2}+(7-x)^{2}-2\cdot8\cdot(7-x)(-\frac{1}{2})$$; $$49+14x+x^{2}=64+49-14x+x^{2}+56-8x$$; $$36x=120$$ $$\Leftrightarrow$$ $$x=\frac{120}{36}=\frac{10}{3}$$ $$\Rightarrow$$ $$KC=7-\frac{10}{3}=\frac{11}{3}$$;
2) По т. Менелая: $$\frac{BE}{ED}\cdot\frac{AD}{AC}\cdot\frac{CK}{KB}=1$$; $$\frac{BE}{ED}\cdot\frac{4}{8}\cdot\frac{11}{3}\cdot\frac{3}{10}=1$$; $$\frac{BE}{ED}=\frac{20}{11}$$ $$\Rightarrow$$ $$\frac{BE}{ED}=\frac{20}{31}$$
3) $$\frac{S_{BEK}}{S_{BDC}}=\frac{BE\cdot BK}{BD\cdot BC}=\frac{20}{31}\cdot\frac{10}{3\cdot7}=\frac{200}{651}$$ $$\Rightarrow$$ $$S_{BEK}=\frac{200}{651}S_{BDC}$$ $$\Rightarrow$$ $$S_{DEKC}=\frac{451}{651}S_{BDC}$$;
4) $$S_{BDC}=\frac{1}{2}S_{ABC}=\frac{1}{2}\cdot\frac{1}{2}\cdot8\cdot7\cdot\frac{\sqrt{3}}{2}=7\sqrt{3}$$; $$S_{DEKC}=\frac{451\cdot7\sqrt{3}}{651}=\frac{451\sqrt{3}}{93}$$
Задание 16
Олигарх Аристарх Луков‐Арбалетов имеет в собственности три частных банка. Активы первого банка состоят на 70% из рублей и на 30% из долларов. Во втором банке 80% активов составляют рубли и 20% – евро; в третьем банке 50% активов в рублях, 10% – в долларах и 40% – в евро. Аристарх планирует открыть 4‐й банк, направив туда часть активов из каждого банка так, чтобы доля каждой валюты в каждом из них сохранилась, а активы нового банка состояли бы ровно на 15% в долларах. Какой наименьший процент рублей могут содержать активы нового банка?
Пусть х - объем денег с первого, тогда рубли $$0,7x$$; доллары - $$0,3x$$. Второй - $$y$$; тогда рубли - $$0,8y$$; $$0,2y$$ - евро, третий - $$z$$, тогда $$0,5z$$ - рубли, доллары - $$0,1z$$, евро - $$0,4z$$. Т.к. во втором долларов нет, то при внесении денег оттуда добавятся только рубли и евро, а т.к. процент рублей больше, чем евро, то по отношению к общей массе денег в четвертом процент рублей увеличится. Тогда из 2го лучше не брать, раз надо минимальный процент рублей в четвертом:
Всего: $$x+y+z$$
Рубли: $$0,7x+0,8y+0,5z$$
Доллары: $$0,3x+0,1z$$
Евро: $$0,2y+0,4z$$
$$\frac{0,3x+0,1z}{x+y+z}=0,15$$ - (15% долларов); $$x+y+z=\frac{0,3x+0,1z}{0,15}$$; $$x+y+z=2x+\frac{2}{3}z$$; $$z=3x-3y$$ $$\Rightarrow$$ $$x>y$$
Функция процента рублей: $$f(x;y;z)=\frac{0,7x+0,8y+0,5z}{x+y+z}=\frac{(0,7x+0,8y+0,5z)\cdot0,15}{0,3x+0,1z}=$$ $$\frac{0,15(0,7x+0,8y+1,5x-1,5y)}{0,3x+0,1(3x-3y)}=\frac{0,15(2,2x-0,7y)}{0,3x+0,3x-0,3y}=$$ $$\frac{2,2x-0,7y}{4x-2y}=0,55+\frac{0,4y}{4x-2y}$$
Задание 17
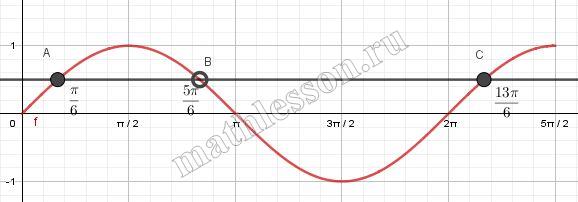
Найдите все $$a$$, при каждом из которых уравнение $$\log{\frac{1,2x}{\pi}}(2\sin^{2}x-4a\sin x-\sin x+2a+1)=0$$ имеет не более трёх корней, входящих в отрезок $$[-\frac{\pi}{2};\frac{5\pi}{2}]$$
$$\left\{\begin{matrix}2\sin^{2}x-4a\sin x-\sin x+2a+1>0\\\frac{1,2x}{\pi}>0\\x\in[-\frac{\pi}{2};\frac{5\pi}{2}]\\2\sin^{2}x-4a\sin x-\sin x+2a+1=1\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}2\sin^{2}x-4a\sin x-\sin x+2a+1=0(1)\\x\in(0;\frac{5\pi}{2})\cup{\frac{5\pi}{6}}\end{matrix}\right.$$
1) $$2\sin^{2}x-\sin x(4a+1)+2a=0$$
$$D=16a^{2}+8a+1-16a=(4a-1)^{2}$$; $$\sin x=\frac{4a+1\pm|4a-1|}{2}=2a;\frac{1}{2}$$; $$\sin x=\frac{1}{2}$$ $$\Leftrightarrow$$ $$x=(-1)^{n}\frac{\pi}{6}+\pi n,n\in Z$$; $$\sin x=2a$$ $$\Leftrightarrow$$ $$x=(-1)^{n}\arcsin2a+\pi n,n\in Z$$
$$\sin x=\frac{1}{2}$$ дает с учетоа ОДЗ 2 корня: $$(\frac{\pi}{6};\frac{13\pi}{6})$$, значит $$\sin x=2a$$ не более одного отличного решения $$\Rightarrow$$ $$2a\in(-\infty;-1]\cup{\frac{1}{2}}\cup(1;+\infty)$$ $$\Rightarrow$$ $$a\in(-\infty;-\frac{1}{2}]\cup{\frac{1}{4}}\cup(\frac{1}{2};+\infty)$$
Задание 18
Даны 20 чисел: 2, 3, 4,…, 20, 21.
a) Выпишем все числа: 2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21. Из них простых - 8: 2,3,5,7,11,13,17,19. Остальные составные $$\Rightarrow$$ делятся на 1 из предыдущих минимум 8
б) Т.к, необходимо взять 8 чисел есть несколько возможных вариантов. Можно взять все 8 простых и 4 составных. Но если взять 8 простых, то из 12 оставшихся только 3 нечетных, то есть минимум 1 четное $$\Rightarrow$$ делится на 2. Значит не подойдет.
Брать разные числа, но каждое из первых десяти чисел будет делителем хотя бы для одного из следующих 10ти (т.к. однозначное, умноженное на 2,в любом случае не больше 20) $$\Rightarrow$$ из 12 чисел хотя бы 1 будет однозначным $$\Rightarrow$$ делителем $$\Rightarrow$$ ответ: нет.
в) сумма квадратов n-первых натуральных чисел: $$p(n)=\frac{n(n+1)(2n+1)}{6}=\frac{21\cdot22\cdot43}{6}=3311$$; т.к. 1 не входит, то 3310 $$\Rightarrow$$ в каждом по 1655.
$$21^{2}+20^{2}+19^{2}+18^{2}=1526$$ $$\Rightarrow$$ осталось 129
$$10^{2}+5^{2}+2^{2}=129$$ $$\Rightarrow$$ в певрвой: 2,5,10,18,19,20,21
во второй: 3,4,6,7,8,9,11,12,13,14,15,16,17.