269 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.

Одного рулона обоев хватает для оклейки полосы от пола до потолка шириной 1,2 м. Сколько рулонов обоев нужно купить для оклейки прямоугольной комнаты размерами 3,3 м на 4,2 м?

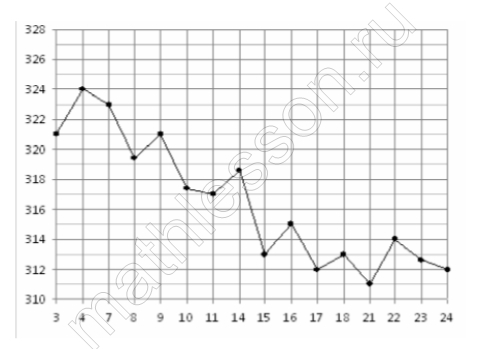
На рисунке точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 3 по 24 октября 2002 года. По горизонтали указываются числа месяца, по вертикали – цена унции золота в долларах США. Для наглядности точки на рисунке соединены линией. Определите по рисунку наибольшую цену золота на момент закрытия торгов в период с 15 по 23 октября (в долларах США за унцию).

Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/π.

Из множества натуральных чисел от 58 до 82 наудачу выбирают одно число. Какова вероятность того, что оно делится на 6?

На сторонах AB и BC треугольника ABC выбраны соответственно точки P и Q так, что BP:PA=1:2 и BQ:QC=4:1. Найдите отношение площади четырёхугольника ACQP к площади треугольника PBQ.

Прямая, изображенная на рисунке, является графиком одной из первообразных функции y=f(x). Найдите f(2).

Расстояние от вершины основания правильной треугольной пирамиды до плоскости боковой грани, не содержащей эту вершину, равно 3,5. Высота основания пирамиды равна 5. Найдите синус угла между плоскостью боковой грани и плоскостью основания пирамиды.

Найдите значение выражения $$\sqrt[4]{17+12\sqrt{2}}\cdot \sqrt{3-2\sqrt{2}}$$

Автомобиль, движущийся в начальный момент времени со скоростью v₀ =15 м/с, начал торможение с постоянным ускорением a = 2 м/с² . За t секунд после начала торможения он прошёл путь $$S=v_{0}t-\frac{at^{2}}{2}$$ (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 36 метров. Ответ выразите в секундах.

Бригада, состоящая из двух рабочих 4‐го разряда и трёх рабочих 5‐го разряда, выполняет работу за два часа. Если к этой бригаде добавить ещё двух рабочих 4‐го разряда, то работа будет выполнена за полтора часа. Сколько рабочих 4‐го разряда нужно добавить к этой бригаде, чтобы работа была выполнена за 1 час?

Найдите наименьшее значение функции $$y=7^{x-3}+7^{5-x}$$

В правильной четырехугольной пирамиде SABCD точка Р – середина ребра SA, точка Q – середина ребра SC.

Решите неравенство $$\log_{3} (3^{x}-1)\cdot \log_{9} (9^{x+2}-6\cdot 3^{x+3}+81)<3$$

В параллелограмме ABCD проведена диагональ АС. Точка О является центром окружности, вписанной в треугольник АВС. Расстояния от точки О до точки А и прямых AD и AC равны соответственно 10, 8 и 6.

15 января планируется взять кредит в банке на сумму 600 тыс. рублей на 24 месяца. Условия его возврата таковы:

• 1‐го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
• со 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;
• 15‐го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15‐е число предыдущего месяца.

На сколько рублей увеличится сумма выплат, если взять кредит с такими же условиями на 30 месяцев?

Найдите все значения параметра a, при каждом из которых система уравнений $$\left\{\begin{matrix}a(x+2)+y=3a\\ a+2x^{3}=y^{3}+(a+2)x^{3}\end{matrix}\right.$$ имеет не более двух решений

На доске было написано 20 натуральных чисел (не обязательно различных), каждое из которых не превосходит 40. Вместо нескольких (возможно, одного) из чисел на доске написали числа, меньшие первоначальных на 1. Числа, которые после этого оказались равными 0, с доски стёрли.