ЕГЭ математика 2018. Разбор варианта Алекса Ларина № 208
Решаем ЕГЭ вариант Ларина № 209. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,13,14,15 заданий тренировочного варианта ЕГЭ Ларина № 208 (alexlarin.com)
Решаем ЕГЭ вариант Ларина № 209. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина № 208 (alexlarin.com)
Задание 1
На автозаправке клиент залил в бак 45 литров бензина по цене 36 руб. 60 коп. за литр, и отдал кассиру пятитысячную купюру. Сколько рублей сдачи он должен получить у кассира?
$$36,6\cdot45=1647$$ $$5000-1647=3353$$
Задание 3
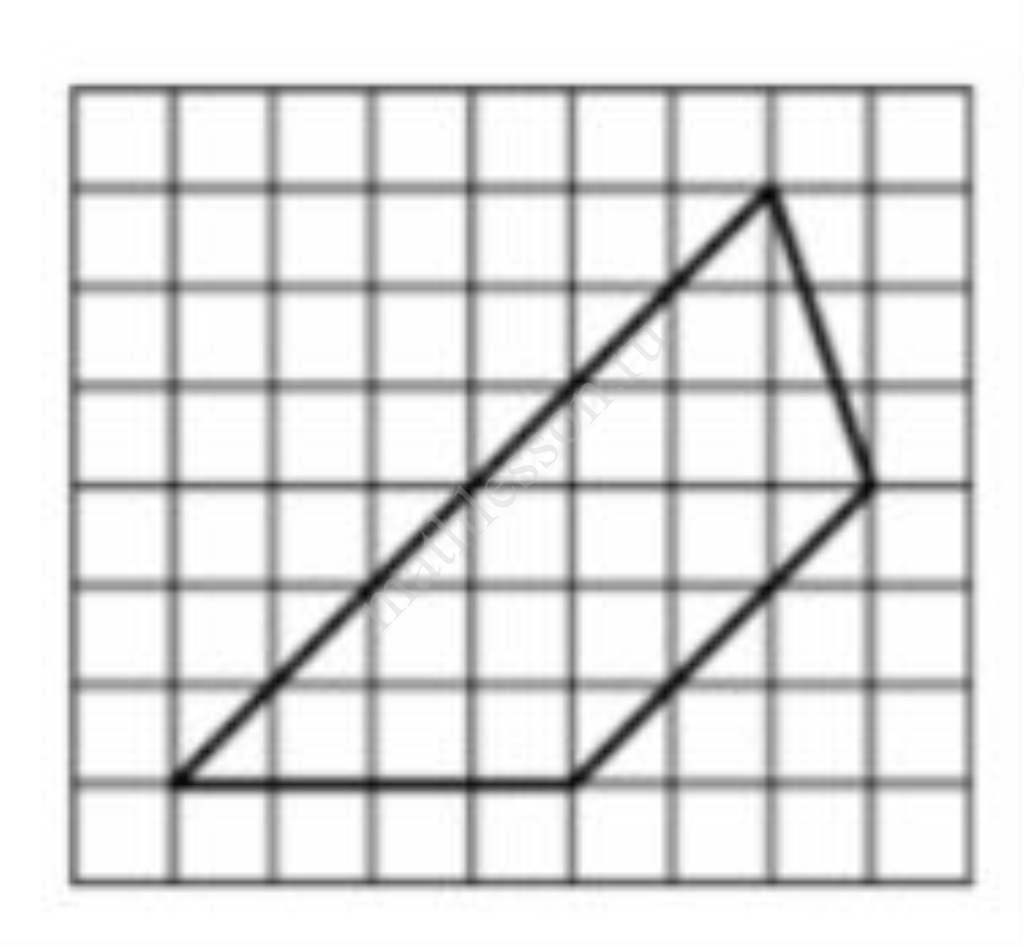
Найдите площадь трапеции, изображённой на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
$$S=6\cdot7-\frac{1}{2}\cdot6\cdot6-\frac{1}{2}\cdot3\cdot3-\frac{1}{2}\cdot3\cdot1=42-18-4,5-1,5=18$$
Задание 4
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Космос» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Космос» начнёт игру с мячом все три раза.
Всего соперников 3. Всего событий на матч 2 (начнет первой или не начнет первой). Всего возможных исходов: $$N=2^{3}=8$$. Вероятность, что 3 раза будет первой: $$P=\frac{1}{8}=0,125$$
Задание 5
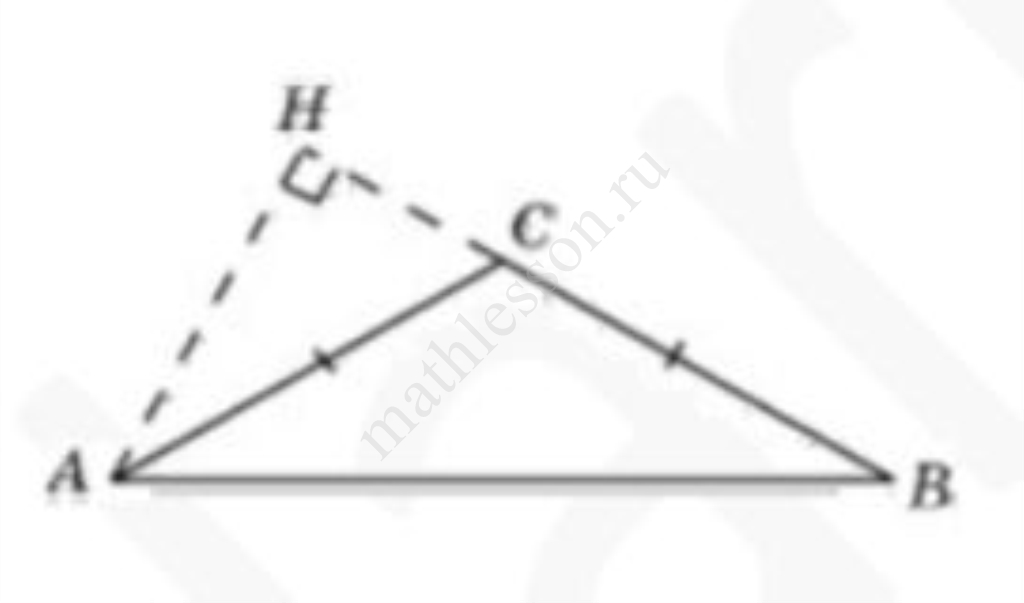
$$\angle HCA=180^{\circ}-\angle ACB=60^{\circ}$$ из $$\bigtriangleup AHC$$: $$AH=AC\sin ACH=2\sqrt{3}\cdot\frac{\sqrt{3}}{2}=3$$
Задание 6
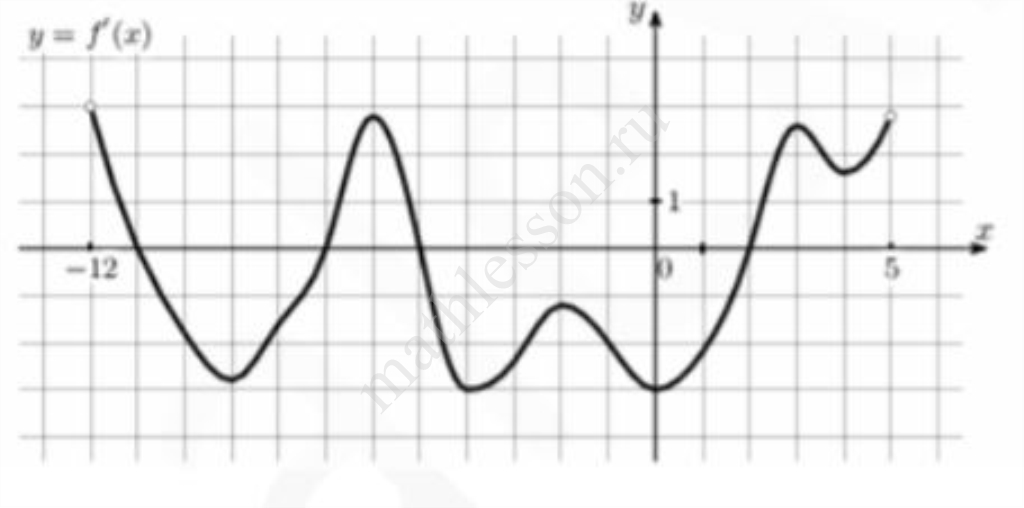
На рисунке изображен график y=f′(x) - производной функции f(x), определенной на интервале (-12;5). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-10;4].
$$-7; 2$$ $$\Rightarrow$$ 2 точки
Задание 7
$$S=2\cdot5+2\cdot5+2\cdot2+2\cdot2+5\cdot4+$$ $$+2\cdot6+2\cdot3+2\cdot3\cdot3+5\cdot3+$$ $$+5\cdot3+2\cdot3+5\cdot6=156$$
Задание 8
Найдите значение выражения: $$\frac{\sqrt{2,8}\cdot\sqrt{2,52}}{\sqrt{0,4}}$$
$$\frac{\sqrt{2,8}\cdot\sqrt{2,52}}{\sqrt{0,4}}=$$ $$=\sqrt{\frac{\frac{28}{10}\cdot\frac{252}{100}}{\frac{4}{10}}}=$$ $$=\frac{28\cdot252}{4\cdot100}=\sqrt{\frac{7\cdot4\cdot7\cdot9}{100}}=$$ $$=\frac{7\cdot2\cdot3}{10}=4,2$$
Задание 9
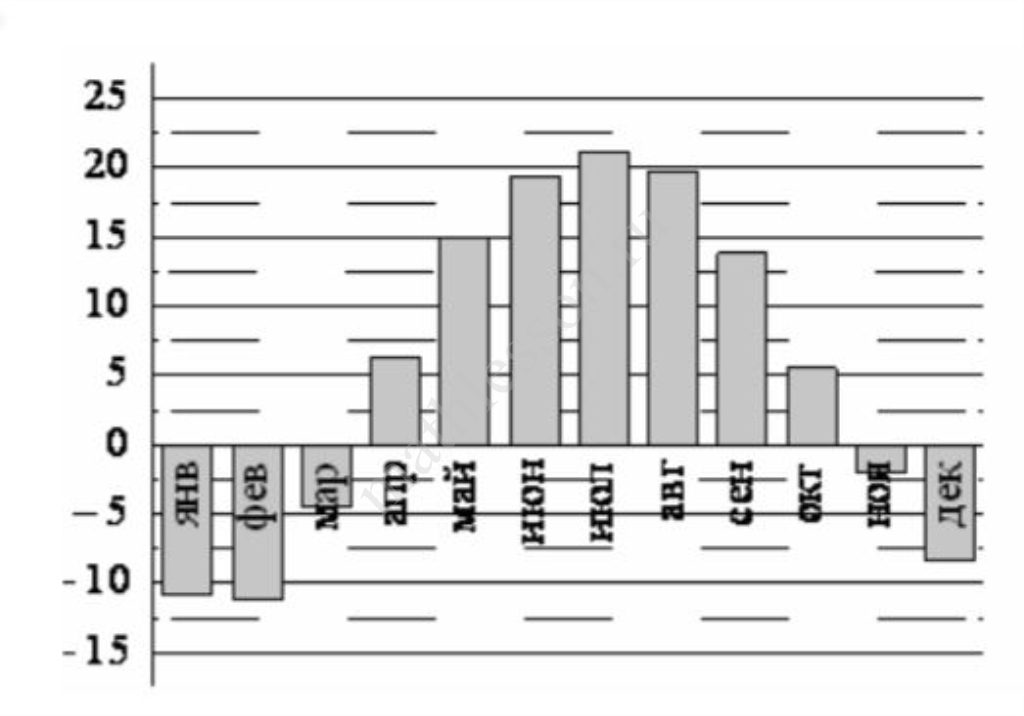
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала f0 = 150 Гц и определяется следующим выражением $$f=f_{0}\cdot\frac{c+u}{c-v}$$ (Гц), где c — скорость распространения сигнала в среде (в м/с), а u=10 м/с и v=15 м/с — скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет не менее 160 Гц?
$$160=150\cdot\frac{c+10}{c-15}$$ $$16=\frac{15\cdot(c+10)}{c-15}$$ $$16c-15\cdot16=15c+15\cdot10$$ $$16c-15c=15\cdot16+15\cdot10$$ $$c=15\cdot26=390$$
Задание 10
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Пусть расстояние до С равно у км, тогда СВ=150-у км. Пусть скорость автомобиля х км/ч, тогда скорость, с которой мотоцикл догоняет автомобиль 90-х км/ч, а расстояние между ними к моменту выезда мотоцикла: $$x\cdot0,5=0,5x$$ км. $$\left\{\begin{matrix}\frac{y}{x}-\frac{y}{90}=\frac{1}{2}\\\frac{150-y}{x}=\frac{y}{90}\end{matrix}\right.$$ $$\Leftrightarrow$$ $$y(\frac{1}{x}-\frac{1}{90})=\frac{1}{2}$$ $$y\cdot\frac{90-x}{x\cdot90}-\frac{1}{90})=\frac{1}{2}$$ $$y=\frac{90\cdot x}{2(90-x)}=\frac{45x}{90-x}$$ $$\frac{150-\frac{45x}{90-x}}{x}=\frac{\frac{45x}{90-x}}{90}$$ $$\frac{150(90-x)-45x}{x(90-x)}=\frac{45x}{(90-x)90}$$ $$150\cdot90(90-x)-45\cdot90\cdot x=45x^{2}$$ |:45 $$150\cdot2(90-x)-90x=x^{2}$$ $$27000-300x-90x=x^{2}$$ $$x^{2}+390x-27000=0$$ $$D=152100+108000=260100=510^{2}$$ $$x_{1}=\frac{-390+510}{2}=60$$ $$x_{2}<0$$ $$y=\frac{45\cdot 60}{90-60}=\frac{45\cdot 60}{30}=90$$
Задание 11
Найдите наибольшее значение функции $$y=x^{5}+20x^{3}-65x$$ на отрезке [-4; 0].
$$y=x^{5}+20x^{3}-65x$$ [-4; 0] $${y}'=5x^{4}+60x^{2}-65=0$$ $$x^{4}+12x^{2}-13=0$$ пусть $$x^{2}=a$$ $$a^{2}+12a-13=0$$ $$a_{1}=1$$ $$a_{2}=-13$$ $$\left\{\begin{matrix}x^{2}=1\\x^{2}=-13\end{matrix}\right.$$ $$\Leftrightarrow$$ $$\left\{\begin{matrix}x=\pm 1\\x=\varnothing\end{matrix}\right.$$ $$y(-1)=(-1)^{5}+20\cdot(-1)^{3}-65\cdot(-1)=-1-20+65=44$$
Задание 13
Задание 16
В двух коробках лежат карандаши: в первой красные, во второй ‐ синие, причем, красных было меньше, чем синих. Сначала 40% карандашей из первой коробки переложили во вторую. Затем 20% карандашей, оказавшихся во второй коробке, переложили в первую, причем половину из переложенных карандашей составляли синие. После этого красных карандашей в первой коробке оказалось на 26 больше, чем во второй, а общее количество карандашей во второй коробке увеличилось по сравнению с первоначальным более, чем на 5%. Найдите общее количество синих карандашей.
Пусть в первой коробке было $$x$$ красных, а во второй $$y$$ синих. После первого перекладывания стало $$0,6x$$ и $$y+0,4x$$. После второго в первой коробке стало красных $$0,6x+0,1(y+0,4x)$$, во второй красных стало $$0,4x+0,1(y+0,4x)$$. Из условия получаем
$$0,6x+0,1(y+0,4x)=26+0,4x-0,1(y+0,4x)$$; $$x<y$$; $$0,8(y+0,4x)> 1,05y$$.
Из первого находим $$y+1,4x=130$$,$$ y=130-1,4x$$, откуда $$x$$ кратно 5 и не превосходит 90.
Кроме того $$y+0,4x$$ кратно 10, откуда $$x$$ кратно 10.
Из второго находим $$x<130-1,4x$$, откуда $$x\leqslant 54$$
Из последнего находим $$0,8(130-x)>1,05(130-1,4x)$$, $$0,67x>32,5, x\geqslant 49$$
Значит, $$x=50$$.
Тогда $$y=60$$ и все условия задачи выполнены.
Задание 18
а) да, например $$1; 1\frac{1}{9};...$$
б) Нет. Два из этих 29 членов были бы соседними, тогда разность прогрессии была бы целой, а тогда и все остальные члены прогрессии были бы целыми.
в) Заметим что прогрессия $$0;\frac{1}{k};\frac{2}{k};...;\frac{49}{k}$$ содержит ровно $$[\frac{49}{k}]+1$$. Это позволяет сразу привести примеры:
Для 1 числа можно взять $$k=50$$.
Для 2 можно взять $$k=49$$.
Продолжая, подберем $$k=24,16,12,9,8,7,6,5$$ для всех чисел до 10.
Допустим можно сделать прогрессию ровно с 11 целыми членами. Разобьем ее на 10 блоков по 5 чисел. Два целых попадут в один блок, поэтому разница между ними не превосходит $$4d$$, где $$d$$ — разность прогрессии. Но тогда в каждых четырех подряд членах прогрессии попадается целое число, а 50 чисел можно разбить на 12 четверок и еще два числа.