402 вариант Алекса Ларина. Разбор ЕГЭ математика 2023.
Больше разборов на моем ютуб-канале
Задание 1
Задание 2
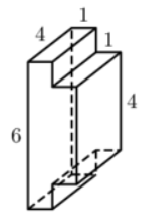
Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4:
$$S=2(4\cdot1+6\cdot1+4\cdot6)+2(4\cdot1+4\cdot1+4\cdot4)-2(4\cdot4)=84$$
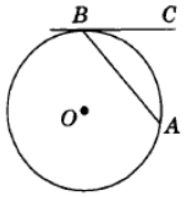
Задание 3
Сначала определим вероятность того, что было куплено яйцо высшего сорта у первого или второго хозяйства. Пусть событие $$A$$ означает яйцо высшей категории, а события $$B_1$$ и $$B_2$$ определяют то, что яйцо высшей категории было произведено 1-м и 2-м хозяйством соответственно. Тогда условные вероятности $$P(A|B_1)$$ и $$P(A|B_2)$$ будут означать, вероятности закупки яйца первой категории у 1-го и 2-го хозяйства соответственно. По формуле полной вероятности найдем вероятность того, что будет куплено яйцо высшей категории, имеем:
$$P(AB_1)+B(AB_2)=P(A|B_1)\cdot P(B_1)+P(A|B_2)\cdot P(B_2)=$$
$$=0,35\cdot P(B_1)+0,6\cdot(1-P(B_1))=-0,25\cdot P(B_1)+0,6$$
По условию задачи эта вероятность равна 0,55, следовательно, вероятность того, что купленное яйцо произведено в первом хозяйстве, равна:
$$P(B_1)=(0,55-0,6):(-0,25)=0,2$$.
Задание 4
Предположим, что бросали первый кубик. Тогда вероятность того, что в каком-то порядке выпали 4 и 6 очков, равна $$\frac{1}{6}\cdot\frac{1}{6}+\frac{1}{6}\cdot\frac{1}{6}=\frac{1}{18}.$$
Теперь предположим, что бросали второй кубик. Поскольку на втором кубике числа 4 и 6 встречаются по два раза, вероятность того, что в каком-то порядке выпали 4 и 6 очков, равна $$\frac{2}{6}\cdot\frac{2}{6}+\frac{2}{6}\cdot\frac{2}{6}=\frac{2}{9}.$$
Таким образом, искомая вероятность равна $$\frac{\frac{1}{18}}{\frac{1}{18}+\frac{2}{9}}=\frac{1}{1+4}=0,2.$$
Задание 5
$$\sqrt[x]{64}-\sqrt[x]{2^{3x+3}}+12=0$$
$$\sqrt[x]{2^6}-\sqrt[x]{2^{3x+3}}+12=0$$
$$(\sqrt[x]{2^3})^2-2^{3}\cdot\sqrt[x]{2^3}+12=0$$
Замена: $$\sqrt[x]{2^3}=y>0$$
$$y^2-8y+12=0\Rightarrow (y-2)(y-6)=0\Rightarrow\left[\begin{matrix} y=2\\ y=6 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} \sqrt[x]{2^3}=2\\ \sqrt[x]{8}=6 \end{matrix}\right.\Leftrightarrow x=3$$
Предполагается, что $$x\in N,$$ поэтому $$\sqrt[x]{8}=6$$ не имеет решений.
Задание 6
$$\frac{5\sin a-4\cos a-2}{5\sin a+\cos a-3}=\frac{2}{3}\Leftrightarrow 15\sin a-12\cos a-6=10\sin a+2\cos a-6\Rightarrow$$
$$\Rightarrow5\sin a=14\cos a\; |:\cos a\Rightarrow 5\tg a=14\Rightarrow \tg a=2,8$$
Задание 7
На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наименьшее значение функции достигается на правой границе отрезка, т. е. в точке $$1.$$
Задание 8
Необходимо рассчитать значение $$t,$$ при котором $$l(t)=l_0+3\cdot10^{-3}$$ метров. Воспользуемся законом изменения длины рельс от температуры и выразим температуру, получим:
$$l_0+3\cdot10^{-3}=l_0+l_0at$$
$$l_0at=3\cdot10^{-3}$$
$$t=\frac{3\cdot10^{-3}}{l_0a}$$
$$t=\frac{3\cdot10^{-3}}{10\cdot1,2\cdot10^{-5}}=\frac{3\cdot10^{-3}}{12\cdot10^{-5}}=25$$
Задание 9
Необходимо понять, как протекает данный процесс.
За точку, которая передвигается, принимается нос второго сухогруза. В таком случае он проходит сначала расстояние 300 метров, потом длину первого 120 метров, потом свою длину 80 метров, и только с этого момента начинает его опережать, то есть проходит еще 300 метров. В таком случае общий путь S=800 метров = 0,8 км.
Далее можно рассмотреть эту задачу немного иначе.
Раз один догоняет другого, мы можем представить, что первый стоит, а второй двигается к нему со скоростью, равной разности их скоростей, то есть то, что мы ищем.
Время представляем в часах: 0,2 часа и далее применяем стандартную формулу нахождения скорости через расстояние и время.
Получаем: $$v=\frac{0,8}{0,2}=4$$
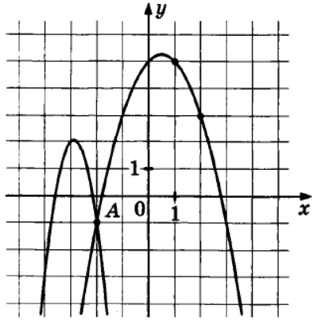
Задание 10
Очевидно, что это правый график (у $$f(x)$$: $$a=-4$$ - сужение как у левого). $$g(x)$$ проходит через $$(2;3)$$ и $$(1;5).$$ Получим:
$$\left\{\begin{matrix} 3=a\cdot2^2+b\cdot2+5\\ 5=a\cdot1^2+b\cdot1+5 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4a+2b=-2\\ a+b=0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4a+2b=-2\\ 4a+4b=0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2b=2\\ 4a+4=0 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} b=1\\ a=-1 \end{matrix}\right.$$
Получим $$g(x)=-x^2+x+5.$$ Тогда:
$$-4x^2-23x-31=-x^2+x+5\Leftrightarrow 3x^2+24x+36=0\Rightarrow x^2+8x+12=0\Rightarrow$$
$$\Rightarrow\left[\begin{matrix} x=-2\\ x=-6 \end{matrix}\right.$$
Тогда $$B_x=-6$$
Задание 11
$${y}'=\frac{1}{2\sqrt{2\lg x-1}}*\frac{2}{x\ln 10}-\frac{1}{x\ln10}=0$$
$$\frac{1}{x\ln 10}(\frac{1}{2\sqrt{2\lg x-1}})=0$$
$$\left\{\begin{matrix}x\neq 0 \\\sqrt{2\lg x-1}=1(1)\end{matrix}\right.$$
$$(1): \sqrt{2\lg x-1}=1\Leftrightarrow$$ $$2\lg x-1\leq 1\Leftrightarrow$$ $$2\lg x=2\Leftrightarrow$$ $$\lg x=1\Leftrightarrow x=10$$
$$y(10)=y=\sqrt{2\lg 10-1}-\lg 10=1-1=0$$
Задание 13
Задание 15
| План 1 | - каждый январь долг возрастает на 8% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; - кредит должен быть полностью погашен за три года тремя равными платежами. |
| План 2 | - 1-го числа каждого месяца долг возрастает на 0,8% по сравнению с концом предыдущего месяца; - со 2-го по 18-е число каждого месяца необходимо выплатить часть долга; - 19-го числа каждого месяца со 2-го по 36-й долг должен быть меньше долга на 19-е число предыдущего месяца на одну и ту же сумму; - к 19-му числу 36-го месяца кредит должен быть полностью погашен. |
Задание 16
Задание 18
$$ax^2+bx+c=0$$
$$bx^2+cx+a=0$$
$$cx^2+ax+b=0$$
имеют общий корень. Решите эти уравнения.