261 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 261 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №261 (alexlarin.com)
Решаем ЕГЭ 261 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №261 (alexlarin.com)
Задание 1
В сентябре 1 кг винограда стоил 50 рублей, в октябре виноград подорожал на 20%, а в ноябре еще на 40%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
1) После увеличения на 20% : 50*1,2=60 рублей 2) После увеличения на 40% : 60*1,4=84 рублей
Задание 2
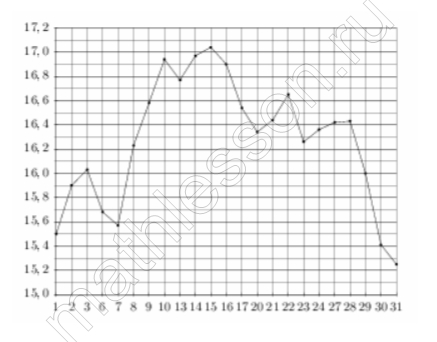
На рисунке жирными точками показана цена серебра, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали — цена серебра в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода цена серебра была больше 16,8 рубля за грамм.
Задание 3
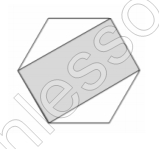
Пусть a – сторона шестиугольника, тогда $$S=\frac{3\sqrt{3}a^{2}}{2}$$ - его площадь . При этом площадь отсеченного треугольника: $$S_{\Delta }=\frac{1}{2} *a*a*\sin 120=\frac{\sqrt{3}a^{2}}{4}$$, тогда $$2S_{\Delta }=\frac{\sqrt{3}a^{2}}{2}=\frac{S}{3}$$. Получаем , что площадь прямоугольника : $$\frac{2S}{3}=\frac{2*72}{3}=48$$
Задание 4
Всего возможных расположений: $$N=3!=1*2*3=6$$, 5 из них не соответствуют первоначальному расположению. Тогда не в том же порядке : $$P=\frac{5}{6}\approx 0,83$$
Задание 5
Решите уравнение $$\sqrt{-2-x}*\sqrt{3-2x}=3$$ . Если уравнение имеет более одного корня, в ответе укажите больший из них.
$$\sqrt{-2-x}*\sqrt{3-2x}=3\Leftrightarrow$$ $$\left\{\begin{matrix}-2-x\geq 0\\3-2x\geq 0\\(-2-x)(3-2x)=9\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\leq -2\\x\leq 1,5\\2x^{2}+x-6-9=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\leq -2\\2x^{2}+x-15=0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\leq -2\\\left[\begin{matrix}x=2,5\\x=-3\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$x=-3$$
Задание 6
Четырёхугольник ABCD вписан в окружность, причём BC =CD. Известно, что угол ADC равен 930 . Найдите, под каким острым углом пересекаются диагонали этого четырёхугольника. Ответ дайте в градусах.
1) $$\angle ADC=93$$, пусть $$\angle CDB=\alpha$$$$\Rightarrow$$ $$\angle CBD =\alpha$$ 2) $$\angle ADB=\angle ADC-\angle CDB=93-\alpha$$ . Но $$\angle ACB=\angle ADB$$(опирают на одну дугу )$$\Rightarrow$$ из $$\Delta CHB$$ ($$AC \cap DB=H$$): $$\angle CHB=180-(93-\alpha +\alpha )=87$$
Задание 7
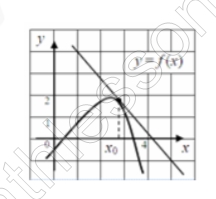
К графику функции у = f (x) проведена касательная. Определите значение производной функции в точке х0
из $$\Delta ABC$$: $$tg \angle CAB =\frac{CB}{AB}=\frac{5}{4}=1,25\Rightarrow$$ $${f}'(x_{0})=-tg\angle CAB=-1,25$$ (т .к. f(x) убывает в $$x_{0}$$)
Задание 8
В правильной шестиугольной пирамиде сторона основания равна $$4\sqrt{3}$$, а высота равна 8. Через высоту пирамиды проведена плоскость. Найдите наименьшую площадь сечения пирамиды такой плоскостью.
1) $$S_{min}=S_{SHM}$$ (т.к. наименьшее основание для сечения только в том случае , когда проходит через середины противоположных сторон); $$S_{SHM}=\frac{1}{2}SO*HM$$
2) Из $$\Delta HOB$$: $$OH=OB \sin B=4\sqrt{3}*\frac{\sqrt{3}}{2}=6$$$$\Rightarrow HM=12$$
3) $$S_{SHM}=\frac{1}{2}*8*12=48$$
Задание 9
Найдите значение выражения $$\sqrt{3\sqrt{2}-\sqrt{6}}*\sqrt{\frac{\sqrt{6}+\sqrt{2}}{\sqrt{3}}}$$
$$\sqrt{3\sqrt{2}-\sqrt{6}}*\sqrt{\frac{\sqrt{6}+\sqrt{2}}{\sqrt{3}}}=$$$$\sqrt{\frac{\sqrt{3}(\sqrt{6}-\sqrt{2})(\sqrt{6}-\sqrt{2})}{\sqrt{3}}}=$$$$\sqrt{6-2}=2$$
Задание 10
При температуре 0 °C рельс имеет длину l0=12,5 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону $$l(t^{o})=l_{0}(1+\alpha t^{o})$$, где $$\alpha=1,2*10^{-5}(C^{o})^{-1}$$ C коэффициент теплового расширения, t⁰ – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ выразите в градусах Цельсия.
Подставим имеющиеся значения (с учетом, что l(t)=12,5+0,006 метров): $$12,5+0,006=12,5(1+1,2*10^{-5}t)\Leftrightarrow$$ $$12,5+6*10^{-3}=12,5+15*10^{-5}t\Leftrightarrow$$ $$t=\frac{6*10^{-3}}{15*10^{-5}}=$$$$\frac{2*10^{2}}{5}=40$$
Задание 11
Катер и плот одновременно отплыли вниз по реке. Пройдя 16 км, катер развернулся и пошел вверх по реке. Пройдя 12 км, он встретился с плотом. Какова собственная скорость катера, если скорость течения реки 4 км/ч? Ответ выразите в км/ч.
Так как катер проплыл вниз по течению 16 км, а вверх -12 км, то они встретились с плотом в 4 км. от старта. Т.к. скорость плота равна скорости течения , то время плота : $$t=\frac{4}{4}=1$$ час( как и время катера) .Пусть x км\ч –собственная скорость катера, тогда:
$$\frac{16}{x+4}+\frac{12}{x-4}=1 \Leftrightarrow$$ $$16x-64+12x+48=x^{2}-16\Leftrightarrow$$ $$x^{2}-28x=0\Leftrightarrow$$ $$\left\{\begin{matrix}x=0\\x=28\end{matrix}\right.$$
Скорость не может быть нулевой $$\Rightarrow$$ 28 км\ч
Задание 12
Найдите наибольшее значение функции $$y=(27-x)\sqrt{x}$$ на отрезке [1;16]
Найдем производную и приравняем к 0: $${y}'={(27-x)}'\sqrt{x}+({x}')(27-x)=0\Leftrightarrow$$ $$-1*\sqrt{x}+\frac{1}{2\sqrt{x}}(27-x)=0\Leftrightarrow$$ $$\frac{-2x+27-x}{2\sqrt{x}}=0\Leftrightarrow$$ $$\frac{-3x+27}{2\sqrt{x}}=0\Leftrightarrow$$ $$\left\{\begin{matrix}x=9\\x>0\end{matrix}\right.$$
x=9 – точка максимума , тогда $$y_{max}=y(9)=(27-9)\sqrt{9}=54$$
Задание 13
A) ОДЗ: $$16x-7-4x^{2}>0\Leftrightarrow$$ $$4x^{2}-16x+7<0\Leftrightarrow$$ $$\left\{\begin{matrix}x>0,5\\x<3,5\end{matrix}\right.$$
Решение: разложим $$\cos 2\pi x=2 \cos^{2} \pi x-1$$; $$\sin^{2} \pi x=1-\cos^{2} \pi x$$. Тогда получим : $$\cos^{2}(\pi x)*\log_{3}(16x-7-4x^{2})=6 \cos^{2} \pi x-3+3-3 \cos^{2} \pi x\Leftrightarrow$$$$\cos^{2} (\pi x)(\log_{3}(16x-7-4x^{2})-3)=0\Leftrightarrow$$$$\left[\begin{matrix} \cos ^{2}(\pi x)=0(1)\\ \log_{3}(16x-7-4x^{2})=3 (2)\end{matrix}\right.$$
(1): $$\cos ^{2}\pi x=0\Leftrightarrow$$ $$\cos \pi x=0\Leftrightarrow$$ $$\pi x=\frac{\pi}{2}+\pi n , n \in Z$$$$\Leftrightarrow$$ $$x=\frac{1}{2}+n , n \in Z$$
(2): $$\log_{3}(16x-7-4x^{2})=3\Leftrightarrow$$ $$16x-7-4x^{2}=27\Leftrightarrow$$ $$4x^{2}-16x+34=0\Leftrightarrow$$$$2x^{2}-8x+17=0\Leftrightarrow$$ $$x=\varnothing$$
С учетом ОДЗ: $$0,5<\frac{1}{2}+n<3,5\Leftrightarrow$$ $$0<n<3 \Rightarrow$$ $$n=1; 2\Rightarrow$$ $$x=1,5; 2,5$$
Б) На промежутке $$[\frac{\pi}{2}; \pi]$$ лежит только 2,5
Задание 14
В правильной треугольной пирамиде ABCD сторона основания АВС равна 12, $$\angle ADB=2 arctg \frac{3}{4}$$ . В треугольнике ABD проведена биссектриса ВА1, а в треугольнике BCD проведены медиана ВС1 и высота СВ1.
A) 1) Пусть DH-высота в $$\Delta ADB$$ $$\Rightarrow$$ $$\angle HDB =arctg\frac{3}{4}\Rightarrow$$ $$tg\angle HDB =\frac{3}{4}=\frac{HB}{DH}$$; $$HB=\frac{AB}{2}=6\Rightarrow$$ $$DH=8\Rightarrow$$ из $$\Delta DHB$$: $$DB=\sqrt{DH^{2}+HB^{2}}=10$$
2) $$\frac{V_{A_{1}B_{1}C_{1}D_{1}}}{V_{ABCD}}=$$$$\frac{A_{1}D*B_{1}D*C_{1}D}{AD*BD*CD}(1)$$
3) из $$\Delta ABD$$: $$\frac{AB}{BD}=\frac{AA_{1}}{A_{1}D}=\frac{12}{10}=\frac{6}{5}\Rightarrow$$ $$A_{1}D=\frac{5}{11}AD$$(по свойству биссектрисы)
4) $$DC_{1}=\frac{1}{2}DC$$ (медиана)
Из $$\Delta BCD$$: $$\cos D=\frac{BD^{2}+CD^{2}-BC^{2}}{2 *BD*CD}=0,28$$$$\Rightarrow$$
Из $$\Delta DB_{1}C$$: $$DB_{1}=0,28 DC\Rightarrow$$ $$DB_{1}=0,28DB$$
5) Пусть DO – высота ABCD.
Из $$\Delta ABC$$: $$CH=CB \sin B=12\frac{\sqrt{3}}2{}=6\sqrt{3}\Rightarrow$$ $$CO=\frac{2}{3} CH=4\sqrt{3}$$
Из $$\Delta DOC$$: $$DO=\sqrt{CD^{2}-OC^{2}}=\sqrt{10^{2}-(4\sqrt{3})^{2}}=\sqrt{52}$$
$$S_{ABC}=\frac{1}{2} *12^{2}*\frac{\sqrt{3}}{2}=36 \sqrt{3}$$
$$V_{ABCD}=\frac{1}{3}*36\sqrt{3}*\sqrt{52}=12\sqrt{156}$$
$$V_{A_{1}B_{1}C_{1}D_{1}}=\frac{5}{11}*\frac{1}{2}*\frac{28}{100}*12\sqrt{156}=$$$$\frac{42}{55}\sqrt{156}=\frac{84\sqrt{39}}{55}$$
Б) Пусть $$A_{1}^{'}$$, $$B_{1}^{'}$$, $$C_{1}^{'}$$ проекция $$A_{1}$$, $$B_{1}$$ и $$C_{1}$$ на (ABC). Тогда :
1) из $$\Delta DAO$$: $$\frac{DA_{1}}{DA}=\frac{OA_{1}^{'}}{OA}=\frac{5}{11}$$
2)из $$\Delta DOC$$: $$\frac{DC_{1}}{DC}=\frac{OC_{1}^{'}}{OC_{1}}=\frac{1}{2}$$
3) из $$\Delta DOB$$: $$\frac{DB_{1}}{DB}=\frac{DB_{1}^{'}}{OB}=\frac{28}{100}=\frac{7}{25}$$
4) $$\frac{S_{A_{1}^{'}OC_{1}^{'}}}{S_{AOC}}=$$$$\frac{OA_{1}^{'}*OC_{1}^{'}}{OA*OC}=$$$$\frac{5}{11}*\frac{1}{2}=\frac{5}{22}$$
$$\frac{S_{OC_{1}^{'}B_{1}^{'}}}{S_{OCB}}=\frac{OC_{1}^{'}*OB_{1}^{'}}{OC* OB}=$$$$\frac{1}{2}*\frac{7}{25}=\frac{7}{50}$$
$$\frac{S_{OA_{1}^{'}B_{1}^{'}}}{S_{OAB}}=\frac{OB_{1}^{'}*OA_{1}^{'}}{OB*OA}=$$$$\frac{7}{25}*\frac{5}{11}=\frac{7}{55}$$
$$S_{AOC}=S_{BOC}=S_{AOB}=\frac{1}{3}S_{ABC}\Rightarrow$$ $$S_{A_{1}^{'}B_{1}^{'}C_{1}^{'}}=\frac{1}{3}(\frac{5}{22}+\frac{7}{50}+\frac{7}{55})*36\sqrt{3}=$$$$12\sqrt{3}*\frac{125+77+70}{550}=$$$$12\sqrt{3}*\frac{272}{550}=\frac{1632\sqrt{3}}{275}$$
Задание 15
Решите неравенство $$\log_{\frac{x-1}{2x-8}} (\frac{x+7}{6})\leq 1$$
ОДЗ: $$\left\{\begin{matrix}\frac{x-1}{2x-8}>0\\\frac{x-1}{2x-8}\neq 1\\\frac{x+7}{6}>0\\2x-8\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\frac{x-1}{x-4}>0\\x-1\neq 2x-8\\x+7>0\\2x\neq 8\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x>4\\x<1\\x\neq 7\\x>-7\\x\neq 4\end{matrix}\right.\Leftrightarrow$$ $$x \in (-7 ;1)\cup (4 ;7)\cup (7;+\infty )$$
Решение: $$\log_{\frac{x-1}{2x-8}}\frac{x+7}{6}\leq \log_{\frac{x-1}{2x-8}}(\frac{x-1}{2x-8})\Leftrightarrow$$ $$(\frac{x+7}{6}-\frac{x-1}{2x-8})(\frac{x-1}{2x-8}-1)\leq 0\Leftrightarrow$$ $$\frac{2x^{2}-50}{6(2x-8)}*\frac{-x+7}{2x-8}\leq 0\Leftrightarrow$$ $$\frac{(x-5)(x+5)(x-7)}{(2x-8)}\geq 0\Leftrightarrow$$ $$\left\{\begin{matrix}(x-5)(x+5)(x-7)\geq 0\\2x-8\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\left[\begin{matrix}\left\{\begin{matrix}x\geq -5\\x\leq 5\end{matrix}\right.\\x\geq 7\end{matrix}\right.\\x\neq 4\end{matrix}\right.$$
С учетом ОДЗ: $$x \in [-5; 1)\cup (4 ;5]\cup (7; +\infty )$$
Задание 16
На катете ML прямоугольного треугольника KLM как на диаметре построена окружность. Она пересекает сторону KL в точке Р. На стороне КМ взята точка R так, что отрезок LR пересекает окружность в точке Q, причем отрезки QP и ML параллельны, KR=2RM и $$ML=8\sqrt{3}$$ .
A) $$1) \angle MPL=90$$ (вписанный и опирается на диаметр); $$\angle QMP=\angle OLP$$ (опираются на одну дугу), $$\angle PQL=\angle PML$$ (аналогично) , но $$\angle PML=\angle QPM$$ (накрест лежащие )$$\Rightarrow$$ $$\angle QPM=\angle QPL\Rightarrow$$ $$QM =PL\Rightarrow$$ $$\angle QLM=\angle PML=\alpha$$
2) $$\Delta PML\sim \Delta KML \Rightarrow$$ $$\angle MKL=\angle PML=\alpha \Rightarrow$$ $$\Delta MKL\sim \Delta RML$$. Пусть $$MR=x \Rightarrow$$ $$RK=2x$$ и $$MK=3x$$ . Из подобия: $$\frac{RM}{ML}=\frac{ML}{MK}\Leftrightarrow$$ $$\frac{x}{8\sqrt{3}}=\frac{8\sqrt{3}}{3x}\Rightarrow$$ $$x=8$$
3) из $$\Delta RML$$: $$RL=\sqrt{MR^{2}+ML^{2}}=\sqrt{8^{2}+(8\sqrt{3})^{2}}=16\Rightarrow$$ $$\sin \alpha =\frac{MR}{RL}=\frac{1}{2}\Rightarrow$$ $$\alpha =30$$
4) из $$\Delta MPL$$: $$PL=ML* \sin \alpha =4\sqrt{3}$$. Из $$\Delta KML:$$ $$KL=\frac{ML}{\sin \alpha }=16 \sqrt{3}\Rightarrow$$ $$KP=12\sqrt{3}$$ и $$LP: PK =1: 3$$
Б) $$MQ=PL=4\sqrt{3}$$
Задание 17
Бригада рабочих выполняет задание за 42 дня. Если бы в бригаде было на 4 человека больше и каждый рабочий бригады работал бы на 1 час в день дольше, то это же задание было бы выполнено не более чем за 30 дней. При увеличении бригады еще на 6 человек и рабочего дня еще на 1 час все задание было бы закончено не ранее чем через 21 день. Определите наименьшую при данных условиях численность бригады, а также продолжительность рабочего дня.
Пусть x часов в день работает один рабочий в день, y человек – рабочих в бригаде. Тогда бригада дает $$xy$$ человеко-часов в день. Задание выполняется за 42 дня, т.е. требует $$42xy$$ человеко-часов (ч\ч). Увеличим количество людей на 4 и часы на 1. Получим $$(y+4)(x+1)$$ ч\ч в день и $$\frac{42 xy}{(y+4)(x+1)}\leq 30$$. Аналогично $$\frac{42 xy}{(y+10)(x+2)}\geq 21$$
Имеем систему: $$\left\{\begin{matrix}42xy\leq 30(y+4)(x+1)\\42xy\geq 21(y+10)(x+2)\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}7xy\leq 5(y+4)(x+1)\\2xy\geq (y+10)(x+2)\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}7xy\leq 5xy+5y+20x+20\\2xy\geq xy+2y+10x+20\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2xy-5y-20x-20\leq 0\\xy-2y-10x-20\geq 0\end{matrix}\right. \Leftrightarrow$$ $$\left\{\begin{matrix}2xy-5y-20x-20\leq 0\\2xy-4y-20x-40\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}2xy-5y-20x-20\leq 0(1)\\-2xy+4y+20x+40\leq 0(2)\end{matrix}\right.$$
Сложим 1 и 2 : $$-y+20\leq 0\Rightarrow$$ $$y\geq 20$$. Т.е минимум 20 человек . подставим y=20 в (1) : $$40x-100-20x-20\leq 0\Leftrightarrow$$ $$x\leq 6 \Rightarrow$$ максимум 6 часов
Задание 18
Найдите все значения параметра b, при каждом из которых для любого a неравенство $$(x-a-2b)^{2}+(y-3a-b)^{2}<\frac{1}{2}$$ имеет хотя бы одно целочисленное решение
$$(x-a-2b)^{2}+(y-3a-b)^{2}<\frac{1}{2} \Leftrightarrow$$ $$(x-(a+2b))^{2}+(y-(3a+b))^{2}<(\frac{\sqrt{2}}{2})^{2}$$, т.е. имеем множество точек внутри окружности радиуса $$\frac{\sqrt{2}}{2}$$ и центром в $$(a+2b; 3a+b)$$ . При этом $$\frac{\sqrt{2}}{2}$$ - половина диагонали квадрата со стороной 1 . Т.е. в данный круг вписан квадрат со стороной 1 . Рассмотрим пример:
Видим по радиусу , что целых значений внутри круга не будет. Тогда и только тогда, когда координаты центра одновременно будут иметь вид: $$(\frac{m+m+1}{2}, \frac{n+n+1}{2})$$,где m и n $$\in Z$$
Если хотя бы одна не имеет вид, то 1 целое точно попадет в круг. Тогда :$$\left[\begin{matrix}a+2b\neq \frac{2m+1}{2}\\3a+b\neq \frac{2n+1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}2a+4b\neq 2m+1\\6a+2b\neq 2n+1\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}6a+12b\neq 6m+3\\6a+2b\neq 2n+1\end{matrix}\right.\Leftrightarrow$$$$10b\neq 6m-2n+2\Leftrightarrow$$$$b\neq \frac{3m-n+1}{5}$$ , где $$m , n \in Z$$
Т.е. с учетом, что $$3m-n+1 \in Z$$ при $$m , n \in Z$$, то $$b \notin \frac{k}{5}, k \in Z$$
Задание 19
A) Все числа, что при возведении в квадрат имеют аналогичную цифру в единицах , как и первоначальное оканчиваются на 0,1,5 или 6 ($$0^{2}=0$$ ;$$1^{2}=1$$; $$5^{2}=25$$; $$6^{2}=36$$). Возьмем число 25: $$25^{2}=625\Rightarrow$$ подходит
Б) Самый простой способ рассмотреть двузначное числа, оканчивающиеся на 1: $$11^{2}=121$$; $$21^{2}=441$$; $$31^{2}=961$$; $$41^{2}=1681$$; $$51^{2}=2601$$; $$61^{2}=3721$$; $$71^{2}=5041$$; $$81^{2}=6561$$; $$91^{2}=8281$$. Видим , что не может .
B) Пусть дано трёхзначное число x. При возведении такого числа в квадрат мы получим числа 4х, 5-ти или 6-ти значимые . Следовательно, чтобы данное $$x^{2}$$ оканчивалось на x должно выполняться условие: $$x^{2}-1000K=x$$, где $$K \in N$$ $$\Leftrightarrow$$ $$x^{2}-x=1000K\Leftrightarrow$$ $$x(x-1)=2^{3}*5^{3}K$$
Следовательно, x и x-1 числа последовательные натуральные, одно из них четное, второе –нет . При этом одно из них вида $$2^{3}*m$$, второе $$5^{3}*n$$, где m и n -делители $$K$$ ($$K_{max }=998$$). Рассмотрим 1 случай: $$x=2^{3}m$$, тогда $$x-1=2^{3}m-1$$ и оно трехзначное кратное 125:
Т.е. одно число равно 376. Рассмотрим 2-ой случай : $$x=5^{3} *n \Rightarrow$$ $$x-1=5^{3} *n-1$$, и оно трехзначное , кратное 8 :
Четыре n не рассматриваем, т.к. x-1 нечетно и не кратно 8 . Получим 2 числа: 376 и 625.