341 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

Минимальное количество соболей по максимальной цене ​$$70\cdot1000=70000$$​ рублей

Максимальное количество собой по минимальной цене ​$$120\cdot500=60000​$$

$$​70000-60000=10000​$$ рублей или $$10$$ тысяч рублей

$$720-480=240$$

По рисунку очевидно как нужно провести медиану к стороне $$BC$$.

По теореме Пифагора ​$$\sqrt{3^2+4^2}=5$$

Всего вариантов выпадение 9:

$$​3+6,6+3,4+5,5+4$$​ – 4 исхода

Благоприятных нам только 2: $$​3+6,4+5​$$

​$$P(A)=\frac{2}{4}=0,5$$

Тут можно догадаться, что один из корней это 0. И это правильно, но в условии подсказка, что корней несколько и это в принципе очевидно, т.к. уравнение 4 степени.

Опять же обычное раскрытие скобок ни к чему хорошему не приведет. Если раскроем 1 и 4 скобку и 2 и 3, то у них будут одинаковые коэффициенты при $$x^2$$ и $$x$$.

​$$(x^2+5x+4)(x^2+5x+6)=24​$$

Пусть ​$$x^2+5x=t​$$

​$$(t+4)(t+6)=24​$$ – это квадратное уравнение легко решается

​$$t=-10​$$

$$​t=0​$$

$$​x^2+5x=-10$$​ – тут нет решений $$D<0$$

​$$x^2+5x=0$$​ отсюда же $$​x=0,x=−5$$

По свойству пересекающихся хорд ​$$AO\cdot OC=DO\cdot OB​$$

​ $$\Delta ADO$$​ подобен ​$$\Delta BCO$$​ (по двум пропорциональным сторонам и углу между ними​ $$\angle ADO=\angle COB$$​)

Значит, $$\angle OBC=\angle DAO=\alpha$$ ​

Искомый угол $$\angle DOA=180°-(\angle\beta+\angle\alpha)$$ ​

​$$\angle ADC=\angle\alpha+\angle\beta$$

​$$\angle DOA=180°-(\angle\beta+\angle\alpha)=180°-93°=87°$$

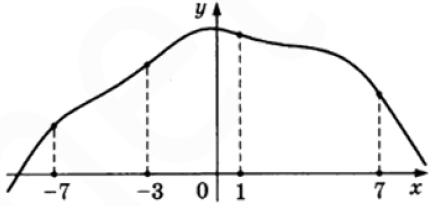
Значение производной будет наименьшим в той точке, где угловой коэффициент касательной будет наименьшим, из рисунка – это точка $$x=7$$

$$(​f'(x_0)=k​)$$

$$S_{внешн}=4πR^2=144π​$$

​$$S_{внутр}=4πr^2=16π​$$

$$​R=6​$$

$$​r=2​$$

​$$d=R−r=4$$

$$\frac{a^{\frac{1}{4}}-a^{\frac{9}{4}}}{a^{\frac{1}{2}}-a^{\frac{1}{3}}}\cdot\frac{a^2}{a^{\frac{3}{2}}+a^{\frac{1}{3}}}=\frac{a^{\frac{1}{4}}(1-a^2)}{a^{\frac{1}{2}}(1-a)}\cdot\frac{a^2}{a^{\frac{3}{2}}+a^{\frac{5}{2}}}=(1+a)\cdot\frac{a^{\frac{7}{4}}}{a^{\frac{3}{2}}+a^{\frac{5}{2}}}=\frac{a^{\frac{7}{4}}(1+a)}{a^{\frac{3}{2}}(1+a)}=$$

$$=\frac{a^{\frac{7}{4}}}{a^{\frac{3}{2}}}=a^{\frac{1}{4}}$$

$$a=16$$

$$16^{\frac{1}{4}}=2$$

$$\frac{M}{1,8^2}=37,5​$$

Откуда ​$$M=121,5​$$

А должна быть масса $$m$$

​$$\frac{m}{1,8}=25$$​, откуда ​$$m=81​$$

Бодибилдеру нужно сбросить ​$$M-m=121,5-81=40,5$$

Легко составить уравнение исходя из условия. Пусть $$x$$​ л второго раствора нужно добавить

в 10 л первого раствора $$0,1\cdot10=1$$​ л вещества

в ​$$x$$​ л второго раствора $$​0,6x​$$

$$​1+0,6x=(x+10)\cdot0,2$$​

Решаем уравнение

$$​x=2,5$$

Найдем критические точки функции

$$y'=0$$​

$$-2\cdot\cos x-(1-2x)\cdot\sin x+2\cos x=0$$​

$$\sin x=0​$$

$$​x=0,5​$$

$$​x=πn​$$

$$​x=0,5​$$

Вспоминаем про промежуток, т.к. ​$$n$$​ - целое, то нам ничего не подходит

$$​x=0,5$$ – точка минимума (это можно проверить с помощью метода интервалов)