360 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Больше разборов на моем ютуб-канале
Задание 1
$$10^{x^2−3}=10^{−2}\cdot10^{3(x−1)}$$
$$x^2−3=3(x−1)−2$$
$$x^2−3x+2=0$$
$$x=1$$
$$x=2$$
Задание 2
Всего $$6\cdot6=36$$ вариантов
Благоприятные {1,1},{1,2},{2,1} – 3 исхода
$$P(A)=\frac{3}{36}\approx0,08$$
Задание 3
Отрезки касательных, проведённые из одной точки, равны.
Значит, по теореме Пифагора:
$$(17x)^2=(5x+6)^2+(12x+6)^2$$, $$(r=6)$$
Решаем квадратное уравнение:
$$\left\{\begin{matrix} x=-\frac{3}{10}\; -\; не\; подходит\; x>0\\ x=2 \end{matrix}\right.$$
$$AC=17x=17\cdot2=34$$
Задание 5
Пусть сторона основания $$a$$
$$OM=\frac{a\sqrt{3}}{6}$$
$$SO=\frac{a\sqrt{3}\cdot\sqrt{23}}{6}=\frac{a\sqrt{69}}{36}$$
$$OC=\frac{a\sqrt{3}}{3}$$
$$SO^2+OC^2=225$$
$$\frac{69a^2}{36^2}+\frac{3a^2}{9}=225$$
$$15=\sqrt{\frac{69a^2}{36}+\frac{3a^2}{9}}$$
$$\sqrt{\frac{81a^2}{36}}=15$$
$$a=10$$
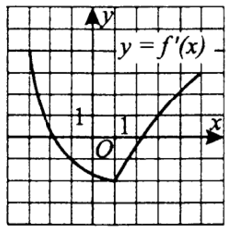
Задание 6
$$f'(3)=1$$ и по геометрическому смыслу производной
$$\tg\alpha=1\Rightarrow$$ угол $$45^{\circ}$$
Задание 7
Задание 8
Пусть $$A$$ - сколько было в бутыли, $$x$$ - сколько отлили
$$0,25A−0,25x=0,12A$$
отсюда $$\frac{x}{A}=0,52$$ – это и есть часть раствора, которая была заменена водой
Задание 9
Составим систему (на рисунке отмечены точки, которые нужно брать)
$$\left\{\begin{matrix} -1=b+\log_a4\\ -2=b+\log_a2 \end{matrix}\right.$$
Вычтем одно из другого
$$\log_a4−\log_a2=1$$
$$\log_a2=1$$
$$a=2$$
$$b=−2−\log_22=−3$$
$$f(x)=−3+\log_2x$$
$$f(32)=−3+\log_232=−3+5=2$$
Задание 10
Тут легче найти обратное.
$$P(B)=0,1\cdot0,1\cdot0,1$$ – все продавцы будут заняты делом
$$P_{иск}=1−0,1^3=0,999$$
Задание 11
Пусть $$t=\frac{5x^2+2}{3x^2+20}$$
$$f(t)=t+\frac{1}{t}$$
$$f'(t)=1−\frac{1}{t^2}$$
Найдем критические точки:
$$f'(t)=0$$
$$\frac{t^2−1}{t^2}=0$$
$$t=−1$$ – точка максимума
$$t=1$$ – точка минимума
$$t=0$$
$$y(1)=2$$