251 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Решаем ЕГЭ 251 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №251 (alexlarin.com)
Решаем ЕГЭ 251 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №251 (alexlarin.com)
Задание 1
Держатели дисконтной карты книжного магазина получают при покупке скидку 4%. Книга стоит 300 рублей. Сколько рублей сдачи получит с 500 рублей держатель дисконтной карты при покупке этой книги?
Скидка с покупки : 300*0,04=12 рублей
Стоимость книги: 300-12-288 рублей
Сдача: 500-288=212 рублей.
Задание 2
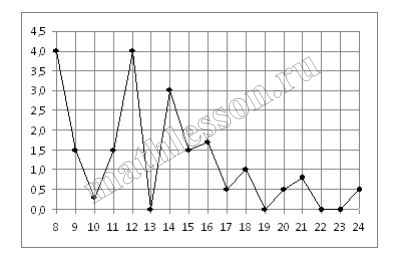
На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.
Задание 3
На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 5. Найдите площадь заштрихованной фигуры.
Радиус большого 3, малого 1 $$\Rightarrow \frac{S_{1}}{S_{2}}=(\frac{3}{1})^{2}=\frac{9}{1}\Rightarrow$$ $$S_{1}=9S_{2}=9*5=45$$ ($$S_{1}$$ - площадь большого , $$S_{2}$$ - площадь малого). Тогда площадь заштрихованной : $$S_{1}-S_{2}=45-5=40$$
Задание 4
В коробке лежат два чёрных, два белых и один красный шар. Из коробки наугад вынимают два шара. Какова вероятность, что вынутые шары окажутся разного цвета?
Найдем вероятность противоположного события - 2 одинаковых, всего шаров 5:
$$4+4 :\frac{2}{5}*\frac{1}{4}=\frac{1}{10}$$
$$5+5: \frac{2}{5}*\frac{1}{4}=\frac{1}{10}$$
Следовательно , $$P_{1}=\frac{1}{10}+\frac{1}{10}=0,2$$
Тогда вероятность 2 разных : $$P=1-P_{1}=1-0,2=0,8$$
Задание 5
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
1) $$\angle BCE=\angle ECD$$ (EC-биссектриса )
$$\angle BCE=\angle CED$$ (накрест лежащие ),тогда $$\Delta CED$$ - равнобедренный и CD=ED=5
2) Аналогично , $$\Delta ABE$$ - равнобедренный , следовательно AB=AE=5
3) $$AD=AE+ED=5+5=10$$
Задание 7
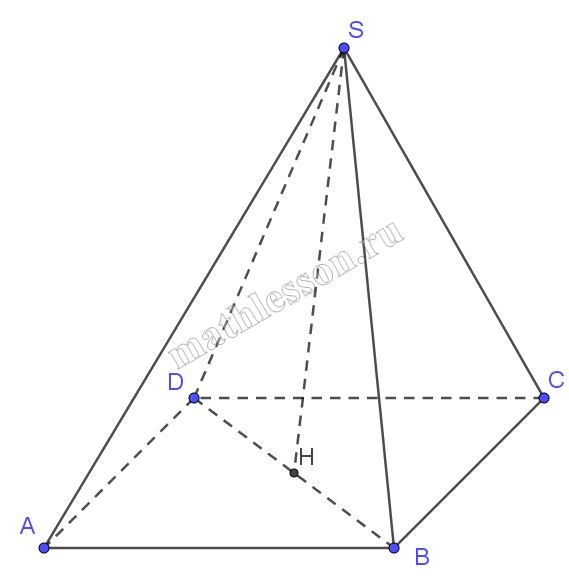
Рассмотрим четырехугольную пирамиду ABCDS с ребром $$3\sqrt{2}$$:
1)$$S_{ABCD}=(3\sqrt{2})^{2}=18$$
2) $$BD=\sqrt{(3\sqrt{2})^{2}+(3\sqrt{2})^{2}}=6\Rightarrow BH=3$$
3) $$\Delta BHS$$: $$SH=\sqrt{(3\sqrt{2})^{2}-3^{2}}=3$$
4) $$V_{ABCDS}=\frac{1}{3}*18*3=18$$
5) Тогда объем октаэдра : $$V=2*V_{ABCDS}=2*18=36$$
Задание 8
Найдите значение выражения $$\log_{2} \frac{1}{3} \log_{3} \frac{1}{5} \log_{5} \frac{1}{2}$$
$$log_{2}\frac{1}{3}*log_{3}\frac{1}{5}*log_{5}\frac{1}{2}=$$$$log_{2}3^{-1}*log_{3}5^{-1}*log_{5}2^{-1}=$$$$-1*log_{2}3*log_{3}5*log_{5}2=$$$$-\frac{1}{log_{3}2}*log_{3}5*\frac{1}{log_{2}5}=$$$$-log_{2}5*\frac{1}{log_{2}5}=-log_{5}5=-1$$
Задание 9
Расстояние (в километрах) от наблюдателя, находящегося на высоте h километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле $$l=\sqrt{2rh}$$ где R = 6400 км – радиус Земли. С какой высоты горизонт виден на расстоянии 16 километров? Ответ выразите в километрах
$$l=\sqrt{2Rh}\Leftrightarrow$$ $$l^{2}=2Rh\Leftrightarrow$$ $$h=\frac{l^{2}}{2R}$$
Найдем высоту $$h=\frac{16^{2}}{2*6400}=$$$$\frac{16*16}{2*64*100}=$$$$\frac{2}{100}=0,02$$ км.
Задание 10
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Пусть x км\ч –разница скоростей сухогрузов. Тогда, точка на носу второго сухогруза пройдет расстояние : 400+120+80+600 метров=1,2 км.( нагнал(400), поравнялись носы (120), опередил (80), удалился (600) ) за 12 минут ($$\frac{12}{60}*\frac{1}{5}$$ часа ):$$\frac{1,2}{\frac{1}{5}}=6$$ км\ч –разница
Задание 11
Найдите наибольшее значение функции $$y=\sin x +9x -9$$ на отрезке [‐ 9; 0].
$$y'=\cos x+9$$ . Т.к. $$\left | \cos x \right |\leq 1$$, то $$\cos x+9>0$$, при всех x. Тогда функция возрастает на всем промежутке и $$y_{max}=y(0)$$: $$y(0)=\sin 0+9*0-9=-9$$
Задание 12
А) $$\sin (\frac{\pi}{2}+2x)-3 \cos (\frac{3 \pi}{2}-x)=1+2 \sin x$$
$$\cos 2x+3 \sin x=1+2 \sin x$$
$$x-2 \sin ^{2}x+3 \sin x -2 \sin x-x=0$$
$$-2 \sin^{2}x+\sin x=0$$
$$\sin x(-2 \sin x-1)=0$$
$$\left\{\begin{matrix}\sin x=0\\\sin x=\frac{1}{2}\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=\pi n , n \in Z\\x=(-1)^{n}\frac{\pi}{6}+\pi n\end{matrix}\right.$$
Б) $$\pi n$$ : $$n=0\Rightarrow 0$$, $$n=1\Rightarrow \pi$$
$$(-1)^{n}\frac{\pi}{6}+\pi n$$ : $$n=0\Rightarrow \frac{\pi}{6}$$, $$n=1\Rightarrow \frac{5 \pi}{6}$$
Задание 13
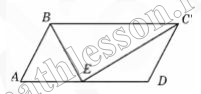
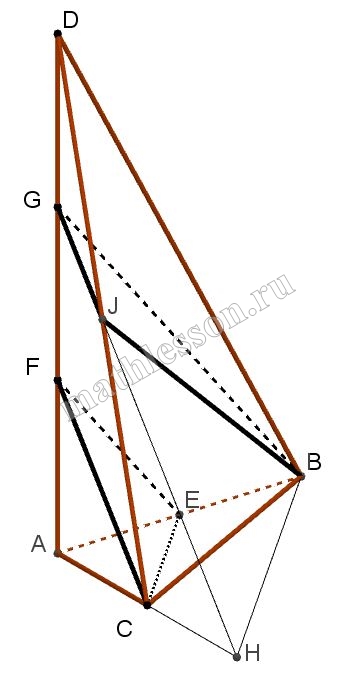
Ребро SA пирамиды SABC перпендикулярно плоскости АВС, ,AB=2, AC=1, $$\angle BAC=120^{\circ}, SA=3\sqrt{2}$$ . Сечения пирамиды двумя параллельными плоскостями, одна из которых проходит через точку С и середину ребра АВ, а другая – через точку В, имеют равные площади.
A) 1) Пусть E-середина $$AB\Rightarrow$$ пусть $$CE\in \alpha$$ и $$\alpha \cap AD=F$$, тогда $$\alpha =(CEF)$$
2)Пусть $$B \in \beta$$ и $$\alpha \left | \right |\beta$$ и $$\beta \cap AD=G$$; $$\beta \cap CD=J$$. Тогда : $$EF\left | \right |BG$$ и т.к. $$\Delta AEF\sim \Delta ABG$$, то $$\frac{AE}{AB}=\frac{EF}{BG}=\frac{1}{2}\Rightarrow$$ $$BG=2 EF(1)$$
3) $$S_{CFE}=S_{JGB}\Rightarrow$$$$\frac{1}{2}CF*FE*\sin F=\frac{1}{2}JG*GB \sin F$$; $$\angle F=\angle G\Rightarrow$$$$CF*FE=JG*GB$$. С учетом (1) получаем, что $$JG=\frac{1}{2}CF$$. Но $$\Delta SGT\sim \Delta SFC\Rightarrow$$ $$\frac{GT}{CF}=\frac{SG}{SF}=\frac{1}{2}\Rightarrow$$ $$AF=FG=GS=\frac{1}{3}AS=\sqrt{2}$$
4) $$V_{FACE}=\frac{1}{3}S_{AEC}*AF=$$$$\frac{1}{3}*\frac{1}{2}*S_{ABC}*\frac{1}{3}AS=$$$$\frac{1}{6}V_{SABC}$$;
$$\frac{V_{SGBJ}}{V_{SABC}}=\frac{SG*SJ*SB}{SA*SC*SB}=$$$$\frac{1}{3}*\frac{1}{2}=\frac{1}{6}\Rightarrow$$ $$V_{SGBJ}=\frac{1}{6}V_{SABC}$$, $$V _{FECGBJ}=\frac{4}{6} V_{SABC}$$; $$V_{SABC}=\frac{1}{3}*\frac{1}{2}*2*1*\frac{\sqrt{3}}{2}*3\sqrt{2}=\frac{\sqrt{6}}{2}$$
Найдем $$V_{FACE}=V_{SGJB}=\frac{\sqrt{6}}{12}$$; $$V_{FCEGBJ}=\frac{4}{6}*\frac{\sqrt{6}}{2}=\frac{2\sqrt{6}}{6}$$
Б) 1)Построим $$AN\perp EC$$ . Опустим перпендикуляр из G на FN :$$GM\perp FN$$ и $$GM\cap FN=G$$. Тогда GMFи FNAявляются одной плоскостью
2) FN\perp CE(по построению) , AN- проекция FN на $$(ABC)\Rightarrow$$ $$CE\perp (FCE)\Rightarrow$$ $$CE\perp MG$$ с учетом , что $$GM\perp FN$$, то $$GM\perp (CEF)\Rightarrow$$ GM - расстояние от (GJB) до (CEF)
3) $$\Delta GFM$$: $$GM=FG \sin \angle MFG$$
$$\angle MFG=\angle AFN$$( вертикальные ), тогда $$\sin \angle MFG=\sin \angle AFN=\frac{AN}{FN}$$
$$\Delta ANC$$: $$AN=\frac{1}{2}AC=\frac{1}{2}$$
$$\Delta AFN$$: $$FN=\sqrt{2+\frac{1}{4}}=\frac{3}{2}$$
$$\sin \angle AFN=\frac{1}{2}:\frac{3}{2}=\frac{1}{3}$$
$$GM=\sqrt{2}*\frac{1}{3}=\frac{\sqrt{2}}{3}$$
Задание 14
Решите неравенство: $$x\log_{\frac{1}{3}} (\frac{1}{3}-x)\geq |x|$$
ОДЗ: $$\frac{1}{3}-x>0\Leftrightarrow$$ $$-x>-\frac{1}{3}\Leftrightarrow$$ $$x<\frac{1}{3}$$
1) При $$x \in (-\infty ;0)$$
$$x \log_{\frac{1}{3}}(\frac{1}{3}-x)\geq -x\Leftrightarrow$$ $$x(\log_{\frac{1}{3}}(\frac{1}{3}-x)+1)\geq 0\Leftrightarrow$$ $$x(\log_{\frac{1}{3}}(\frac{1}{3}-x)*\frac{1}{3})\geq 0\Leftrightarrow$$ $$\log_{\frac{1}{3}} \frac{1}{3}(\frac{1}{3}-x)\leq 0\Leftrightarrow$$ $$(\frac{1}{9}-\frac{1}{3}x-1)(\frac{1}{3}-1)\leq 0\Leftrightarrow$$ $$(-\frac{1}{3}x-\frac{8}{9})\geq 0\Leftrightarrow$$$$-\frac{1}{3}x\geq \frac{8}{9}\Leftrightarrow$$ $$x\leq -\frac{8}{3}$$
2)При $$x \in (0; +\infty )$$
$$x \log_{\frac{1}{3}}(\frac{1}{3}-x)\geq x\Leftrightarrow$$ $$x(\log_{\frac{1}{2}}(\frac{1}{3}-x)-1)\geq 0\Leftrightarrow$$ $$x (\log_{\frac{1}{3}}(\frac{1}{3}-x)*3)\geq 0\Leftrightarrow$$ $$\log_{\frac{1}{3}}(\frac{1}{3}-x)3\geq 0\Leftrightarrow$$ $$(1-3x-1)(\frac{1}{3}-1)\geq 0\Leftrightarrow$$ $$(-3x)\leq 0\Leftrightarrow$$ $$x\geq 0$$
3) При x=0 неравенство выполняется
Тогда решение: $$(-\infty ;-\frac{8}{3})\cup [0;+\infty )$$
С учетом ОДЗ: $$(-\infty;-\frac{1}{3}]\cup [0;\frac{1}{3})$$
Задание 15
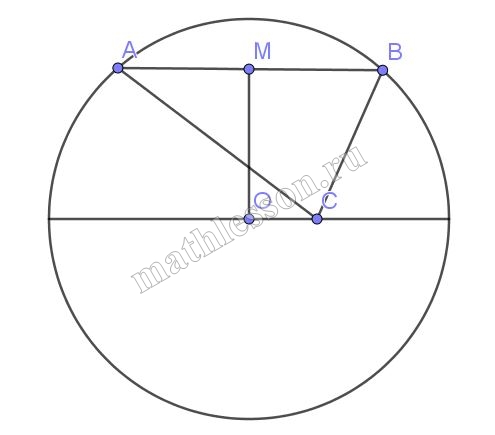
Гипотенуза АВ прямоугольного треугольника АВС является хордой окружности $$\omega$$ радиуса 10. Вершина С лежит на диаметре окружности $$\omega$$ , который параллелен гипотенузе. Угол САВ равен 75.
A) 1) Опустим $$OM\perp AB$$, тогда BM=MA=MC(медиана прямоугольного равна половине гипотенузе)
2) $$\angle MCB=\angle MBC=15$$; $$\angle MBC=\angle BCO=15$$(накрест лежащие) $$\Rightarrow \angle MCO=30$$
3)Пусть $$OM=x\Rightarrow$$ $$MC=2x=BM$$
Из $$\Delta BMO$$ по т. Пифагора : $$BO^{2}=BM^{2}+OM^{2}\Leftrightarrow$$ $$100=x^{2}+4x^{2}=5x^{2}\Leftrightarrow$$ $$x^{2}=20$$
4) $$S_{ABC}=\frac{1}{2}OM*AB=$$$$\frac{1}{2}*x*(2x+2x)=$$$$\frac{1}{2}*4x^{2}=2x^{2}=40$$
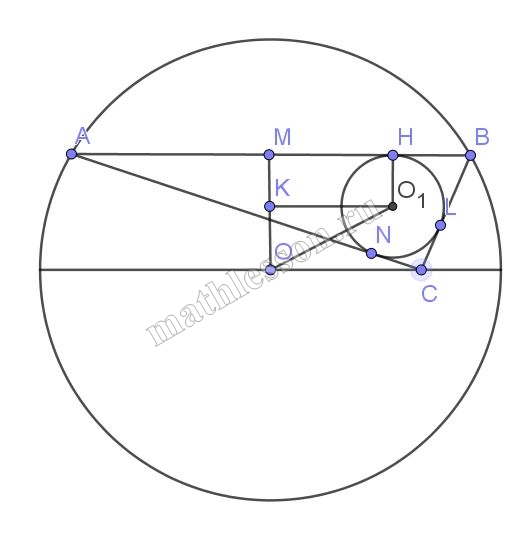
Б) $$1) AB=4x; OM=x, O_{1}$$-центр вписанной . $$O_{1}H; O_{1}C$$-радиусы. Пусть $$O_{1}K\perp OM$$, p - полупериметр $$\Delta ABC$$
2) из $$\Delta ABC: AC=AB \sin B=4x \sin 15$$; $$BC=AB \cos 15=4x \cos 15$$; $$p=\frac{4x+4x\sin 15+4x\cos 15}{2}=$$$$2x+2x \sin 15+2x \cos 15$$
3) Рассмотрим треугольник ABC (прямоуг.); $$p=\frac{AH+AN+CN+LC+LB+BH}{2}$$; $$BH=BL; HA=AN; CL=CN$$
Тогда $$p=\frac{2BL+2CL+2AH}{2}\Leftrightarrow$$ $$p=\frac{2CB+2AH}{2}\Leftrightarrow$$ $$AH=p-CB=2x+2x\sin 15+2x\cos15-4x \cos 15$$, тогда $$MH=MA-HA=KO_{1}$$; $$KO_{1}=2x-(2x+2x\sin 15-2x\cos 15)=$$$$2x\cos 15-2x \sin 15=2x(\cos 15-\sin 15)$$
4) KM=O, H=CN. Аналогично п3: $$CN=p-AB=2x+2x \sin 15+2x\cos 15-4x=$$$$2x\sin 15+2 x\cos 15-2x$$, тогда $$KO=OM-KM=$$$$x-(2x\sin 15+2x \cos 15-2x)=$$$$3x-2x \sin 15-2 x\cos 15=x(3-2(\sin 15+\cos 15))$$
5) $$\Delta KOO_{1}$$: $$OO_{1}=\sqrt{KO^{2}+KO_{1}^{2}}$$
$$KO_{1}=2x(\cos 15-\sin 15)$$; $$x=\sqrt{20}$$
$$\sin 15=\sin (45-30)=\sin 45\cos 30-\cos 45\sin 30=$$$$\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}*\frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$$
$$\cos 15=\cos (45-30)=\cos 45\cos 30+\sin 45\sin 30=\frac{\sqrt{6}+\sqrt{2}}{4}$$
$$KO_{1}=2\sqrt{20}(\frac{\sqrt{6}+\sqrt{2}}{4}-\frac{\sqrt{6}-\sqrt{2}}{4})=$$$$2\sqrt{20}*\frac{\sqrt{2}}{2}=\sqrt{40}$$
$$KO=x(3-2(\sin 15+\cos 15))=\sqrt{20}(3-2(\frac{\sqrt{6}-\sqrt{2}}{4}+\frac{\sqrt{6}+\sqrt{2}}{4}))=$$$$\sqrt{20}(3-2*\frac{\sqrt{6}}{2})=\sqrt{20}(3-\sqrt{6})=3\sqrt{20}-\sqrt{120}$$
$$OO_{1}=\sqrt{(3\sqrt{20}-\sqrt{120})^{2}+(\sqrt{40})^{2}}=$$$$\sqrt{9*20-60\sqrt{24}+120+40}=$$$$\sqrt{180-120\sqrt{6}+160}=\sqrt{340-120\sqrt{6}}=$$$$2\sqrt{5}\sqrt{17-6\sqrt{6}}$$
Задание 16
Цех сборки может выпускать 50 мотоциклов и 150 скутеров в день. Отдел технического контроля в день может проверить не более 75 изделий. Мотоцикл в полтора раза дороже скутера. Сколько мотоциклов и сколько скутеров нужно выпускать в сутки, чтобы общая стоимость продукции была наибольшей и все изделия были проверены отделом технического контроля
Т.к. мотоцикл и скутер являются изделием и стоимость мотоцикла больше, то количесвто мотоциклов возьмем максимальное , т.е. 50, тогда скутеров будет 75-50=25
Задание 17
При каких значениях $$x\neq 0$$ неравенство $$x^{2}(1-\frac{x^{2}a}{x^{2}+a^{2}})-x(1-\frac{x^{2}a}{x^{2}+a^{2}})\geq 0$$ выполняется при любых значениях a
$$x^{2}(1-\frac{x^{2}a}{x^{2}+a^{2}})-x(1-\frac{x^{2}a}{x^{2}+a^{2}})\geq 0\Leftrightarrow$$ $$(x^{2}-x)(1-\frac{x^{2}a}{x^{2}+a^{2}})\geq 0\Leftrightarrow$$ $$\frac{x(x-1)(x^{2}+a^{2}-x^{2}a)}{x^{2}+a^{2}}\geq 0$$
$$x^{2}+a^{2}>0$$, при всех x и a ($$x \neq 0$$). Тогда $$x(x-1)(a^{2}-x^{2}a+x^{2})\geq 0$$
Пусть $$f(x)=x(x-1)$$, $$g(x)=(a^{2}-x^{2}a+x^{2})$$
1) При $$x \in (-\infty ;0)\cup [1; +\infty )(1)$$: $$f(x)>0\Rightarrow$$ $$g(x)>0$$ тоже. Тогда , чтобы выполнилось неравенство для всех a надо, чтобы трехчлен $$a^{2}-x^{2}a+x^{2}$$ (относительно переменной a) был всегда больше или равен $$0\Rightarrow D\leq 0$$:
$$D=x^{4}-4x^{2}\leq 0\Leftrightarrow$$ $$x^{2}(x^{2}-4)\leq 0\Leftrightarrow$$ $$x \in [-2,2]$$. С учетом (1): $$x \in [-2;0)\cup [1;2]$$
2) При $$x \in (0;1), f(x)<0$$.Тогда и $$g(x)<0$$. Но у параболы вида $$f(a)=a^{2}-x^{2}a+x^{2}$$ ветви направлены вверх, то она не может быть меньше 0 при всех x. Следовательно , ответ $$x \in [-2;0)\cup [1;2]$$
Задание 18
S(n) ‐ сумма цифр натурального числа n
A) Пусть $$n=10a+b$$, $$a,b \in N [0;9]$$. Пусть $$a\leq 4$$ и $$b \leq 4$$, тогда $$2n=1-*2a+10*2b$$. Тогда $$a+b=2a+2b\Leftrightarrow$$ $$a+b=0$$,что невозможно . Пусть $$a\leq 4$$ и $$b\geq 5$$, тогда $$2n=10(2a+1)+10(2b-10)$$ и $$a+b=2a+1+2b-10\Leftrightarrow$$ $$a+b=9$$. Су четом условия можно взять числа a=4 и b=5.Значит, может
Б) Аналогично А:
-пусть $$a\leq 4 ;b\leq 4\Rightarrow$$ решений нет
-пусть $$a\leq 4; b\geq 5\Rightarrow a+b=9$$, но тогда a и b не могут быть четными.
-пусть $$a\geq 5, b\leq 4\Rightarrow a+b=9\Rightarrow$$ нет
-пусть $$a\geq 5$$ и $$b\geq 5\Rightarrow$$ $$2n=100*1+10(2a-10+1)+2b-10$$. Тогда $$a+b=18$$. С учетом условия a=8, b=10, но $$a,b \leq 9\Rightarrow$$ нет
B) Аналогично A и Б. Пусть $$n=100a+10b+c$$
1) $$a\leq 4, b\leq 4, c\leq 4\Rightarrow$$ $$a+b+c=0\Rightarrow$$ нет
2) $$a\leq 4, b\leq 4, c\geq 5\Rightarrow$$ $$a+b+c=9$$. Тогда $$a=1,3;b=1,3; c=5,7,9$$. Возможные варианты: 135;117;315 - 3 числа
3) $$a\leq 4; b\geq 5; c\leq 4\Rightarrow a+b+c=9$$. Возможные варианты: $$153;171;351$$ - 3 числа.
4) $$a\leq 4; b\geq 5; c\geq 5\Rightarrow a+b+c=18$$, но a,b,c-нечетные $$\Rightarrow$$ нет чисел
5) $$a\geq 5; b\leq 4; c\leq 4\Rightarrow a+b+c=9$$$$\Rightarrow 513;531;711$$ - 3 числа.
6) $$a\geq 5; b\leq 4; c\geq 5\Rightarrow a+b+c=18$$$$\Rightarrow$$ нет
7) $$a\geq 5; b\geq 5; c\leq 4\Rightarrow a+b+c=18$$$$\Rightarrow$$ нет
8) $$a\geq 5; b\geq 5; c\geq 5\Rightarrow a+b+c=27$$$$\Rightarrow 999$$ - 1 число
Всего получим 10 чисел.