363 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Решаем ЕГЭ 363 вариант Ларина ЕГЭ 2022 по математике. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №363 (alexlarin.com)
Больше разборов на моем ютуб-канале
Аналоги к этому заданию:
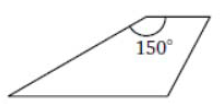
Задание 1
Решите уравнение $$\sin\frac{\pi x}{8}=\frac{\sqrt{2}}{2}.$$ В ответе запишите наибольший отрицательный корень уравнения.
Ответ: -2
Скрыть
$$\frac{πx}{8}=−\frac{π}{4}+2πn$$
$$\frac{πx}{8}=−\frac{3π}{4}+2πn$$
$$x=−2+16n$$
$$x=−6+16n$$
Наибольший отрицательный корень будет при $$n=0$$
$$x=−2$$
$$x=−6$$
Аналоги к этому заданию:
Задание 2
Вася и Петя по дороге в школу садятся на автобус на общей остановке. Вероятность того, что Вася поедет на автобусе в 7:15 равна 2/3 и у Пети так же. А вероятность того, что они поедут вместе на этом автобусе равна 7/12. Найдите вероятность того, что автобус в 7:15 уедет без Пети и без Васи.
(Автор задачи Николай Журавлев)
Ответ: 0,25
Скрыть
$$A$$ - Петя поедет на автобусе
$$B$$ - Вася поедет на автобусе
$$P(A)=\frac{2}{3}$$ - вероятность того, что Петя поедет на автобусе
$$P(B)=\frac{2}{3}$$ - вероятность того, что Вася поедет на автобусе
$$P(AB)=\frac{7}{12}$$ – вероятность того, что они вместе поедут
$$P(A+B)=P(A)+P(B)−P(AB)=\frac{3}{4}$$
$$P_{иск}=1−P(A+B)=\frac{1}{4}=0,25$$
Аналоги к этому заданию:
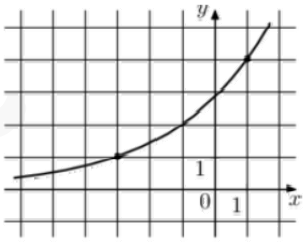
Задание 3
Основания трапеции равны 2 и 5. Боковая сторона, также равная 5, образует с одним из оснований угол 150o. Найдите площадь трапеции.
Ответ: 8,75
Скрыть
Если две параллельные прямые пересечены третьей, то сумма внутренних углов равна 180 (основания трапеции параллельны), значит можно найти второй угол и сразу найти высоту трапеции
$$h=5:2=2,5$$ (как катет лежащий против угла в 30 градусов)
$$S=\frac{2+5}{2}\cdot2,5=8,75$$
Аналоги к этому заданию:
Задание 4
Найдите значение выражения $$g(x-7)\cdot g(7,5-x),$$ если $$g(x)=25^x$$
Ответ: 5
Скрыть
$$25^{x−7}\cdot25^{7,5−x}=25^{x−7+7,5−x}=25^{0,5}=5$$
Аналоги к этому заданию:
Задание 5
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 6. Найдите объем параллелепипеда.
Ответ: 864
Скрыть
$$r=6$$
$$h=6$$
Из рисунка видно, что
$$a=2r$$ ($$a$$ - сторона основания параллелепипеда)
$$V=a\cdot a\cdot h=6\cdot 12\cdot 12=864$$
Аналоги к этому заданию:
Задание 6
На рисунке изображен график $$y=f'(x)$$ - производной функции $$f(x),$$ определенной на интервале $$(-6;8).$$ Сколько можно провести касательных к графику функции $$f(x),$$ которые образуют угол 45o с прямой $$x = 0$$?
Ответ: 8
Скрыть
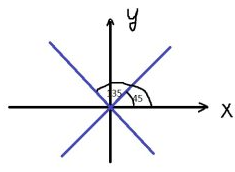
По геометрическому смыслу производной
$$f′(x_0)=\tgα=\tg45=1$$
Но нас будут устраивать две прямые
Т.к они обе образуют с прямой $$x=0$$ угол 45
$$f′(x_0)=\tgα=\tg135=−1$$
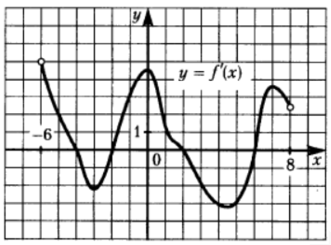
Значит нам нужно найти количество точек пересечения графика с прямой $$y=−1$$ и $$y=1$$
$$\Rightarrow 8$$
Аналоги к этому заданию:
Задание 7
Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона) — устанавливает зависимость между давлением, объёмом и абсолютной температурой m идеального газа. Уравнение имеет вид: $$p\cdot V = \frac{m}{M}\cdot R\cdot T,$$ где $$p$$ - давление (Па), $$V$$ - объем газа (м3), m - масса газа (кг), $$M$$ - молярная масса, $$R = 8,31\frac{Дж}{моль\cdot К}$$ - универсальная газовая постоянная, $$T$$ - абсолютная температура газа (K). Определите температуру (K) кислорода массой 64 г, находящегося в сосуде объёмом 1 л при давлении $$5\cdot10^6$$ Па. Молярная масса кислорода $$M = 0,032$$ кг/моль. Ответ округлите до целого числа.
Ответ: 301
Скрыть
Не забываем переводить в систему СИ
$$m=0,064$$ кг
$$V=10^{-3}$$ $$м^3$$
$$5\cdot10^6\cdot10^{-3}=\frac{0,064}{0,032}\cdot8,31\cdot T$$
$$\Rightarrow T\approx301$$
Аналоги к этому заданию:
Задание 8
Два бегуна одновременно побежали по круговому маршруту из одной ти той же точки в противоположных направлениях. Первый бегун пробежал к месту их встречи на 500 м больше, чем второй. Продолжая бежать в том же направлении, первый прибежал к месту старта через 9 минут после встречи со вторым бегуном, а второй -через 16 минут после встречи. Какова длина кругового маршрута в метрах? Скорости обоих бегунов постоянны.
Ответ: 3500
Скрыть
Пусть скорость первого и второго бегуна $$x,y$$ соответственно
Начнем с рассмотрения условия: “Продолжая бежать в том же направлении, первый пришел к месту старта через 9 минут после встречи со вторым бегуном, а второй – через 16 минут после встречи”
Найдем расстояние пройденное до места старта, после встречи.
$$S_1=9x$$
$$S_2=16y$$
По условию
$$16y−9x=500$$
Осталось найти еще одно уравнение для решения задачи
Это уже можно найти из начала условия задачи
Так как тут круговое движение, то до встречи первый бегун пробегает тот же путь, что и второй бегун пробежит после встречи, и наоборот.
$$S′_1=16y$$
$$S′_2=9x$$
Отсюда время их встречи:
$$t_1=\frac{16y}{x}$$
$$t_2=\frac{9x}{y}$$
$$t_1=t_2$$ – время встречи должно быть одинаково
$$\frac{16y}{x}=\frac{9x}{y}$$
Осталось решить систему любым известным вам способом
Аналоги к этому заданию:
Задание 9
На рисунке изображен график функции $$f(x)=a^{x+b}.$$ Найдите $$f(-7)$$
Ответ: 0,25
Скрыть
Из рисунка видно, какие точки лучше всего взять
$$1=a^{−3+b}$$
$$4=a^{1+b}$$
Можно по-разному решать, один из способов прологарифмировать и поделить одно на другое, выразить $$b$$
Другой способ это умножить первое на 4 и вычесть одно из другого, откуда можно легко выразить $$a$$
$$f(x)=(\sqrt{2})^{x+3}$$
$$f(-7)=0,25$$
Аналоги к этому заданию:
Задание 10
Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Ответ: 0,64
Скрыть
Есть два благоприятных исхода:
1) Первый раз неудача, при второй попытке дозвонились
2) Дозвонились сразу
Эти события несовместны
$$P(A+B)=0,6\cdot0,4+0,4=0,64$$
Аналоги к этому заданию:
Задание 11
Найдите точку максимума функции $$f(x)=x^8\cdot e^{5x+6}.$$
Ответ: -1,6
Скрыть
Найдём критические точки:
$$f'(x)=0$$
$$8x^7e^{5x+8}+x^8\cdot5e^{5x+6}=0$$
$$e^{5x+6}\cdot x^7(8+5x)=0$$
Т.к $$e^x>0$$ всегда
Получаем $$x=0$$
$$x=−\frac{8}{5}=-1,6$$ – точка максимума
Аналоги к этому заданию:
Задание 12
А) Решите уравнение $$(\cos x-\sin x)^2+\sqrt{2}\sin(\frac{3\pi}{4}-2x)+\sqrt{3}\cos x=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-\frac{4\pi}{3};-\frac{2\pi}{3}]$$
Ответ: А)$$\frac{\pi}{2}+\pi n;\pm\frac{5\pi}{6}+2\pi n,n\in Z$$ Б)$$-\frac{7\pi}{6};-\frac{5\pi}{6}$$
Аналоги к этому заданию:
Задание 13
Дан прямой круговой конус с вершиной М. Осевое сечение конуса - треугольник с углом 120o при вершине М. Образующая конуса равна $$6\sqrt{3}.$$ Через точку М проведено сечение конуса, перпендикулярное одной из образующих.
А) Докажите, что получившийся в сечении треугольник - тупоугольный.
Б) Найдите расстояние от центра О основания конуса до плоскости сечения.
Ответ: $$\frac{3\sqrt{3}}{2}$$
Аналоги к этому заданию:
Задание 15
Боря положил некоторую сумму в банк на 4 года под 10% годовых. Одновременно с ним Рома такую же сумму положил на два года в другой банк под 15% годовых. Через два года Рома решил продлить срок вклада еще на два года. Однако к тому времени процентная ставка по вкладам в этом банке изменилась и составляла уже $$x\%$$ годовых. В итоге через 4 года на счету у Ромы оказалась большая сумма, чем у Бори, причем эта разность составила менее 10% от суммы, вложенной каждым первоначально.
Найдите наибольшее возможное целое значение процентной ставки $$x.$$
Ответ: 8
Аналоги к этому заданию:
Задание 16
На стороне КМ остроугольного треугольника РКМ ($$РК\neqРМ$$) как на диаметре построена полуокружность, пересекающая высоту PS в точке Т, PS=8, TS=6, Н - точка пересечения высот треугольника РКМ.
А) Найдите РН.
Б) Полуокружность пересекает стороны РК и РМ в точках L и N соответственно. Найдите коэффициент подобия треугольников PKM и PNL, если радиус полуокружности равен 20.
Ответ: А)$$3,5$$ Б)$$\frac{\sqrt{6449}}{7}$$