366 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Решаем ЕГЭ 366 вариант Ларина ЕГЭ 2022 по математике. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №366 (alexlarin.com)
Больше разборов на моем ютуб-канале
Аналоги к этому заданию:
Задание 1
Решите уравнение $$x^2-\sqrt{(x-1)^2}=1.$$ Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Ответ: -2
Скрыть
ОДЗ:
$$x^2−1\geq0$$
$$x^2−|x−1|=1$$
$$|x−1|=x^2−1$$
Раскрываем модуль:
1. $$x−1\geq0$$
$$x−1=x^2−1$$
$$x=0$$ – не подходит
$$x=1$$
2. $$x−1<0$$
$$−x+1=x^2−1$$
$$x=−2$$
$$x=1$$ – не подходит
$$-2<1$$
Аналоги к этому заданию:
Задание 2
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Ответ: 0,63
Скрыть
$$A$$ - событие, в сумме 4 очка
$$B$$ – сделан 1 бросок
Нужно найти $$P(B|A)=?$$
$$P(B|A)=\frac{P(BA)}{P(A)}$$
$$P(BA)=\frac{1}{6}$$ (при 1 броске выпало 4 очка)
$$P(A)=\frac{1}{6}+\frac{3}{6^2}+\frac{3}{6^3}+\frac{1}{6^4}$$ (при 1 броске выпало 4 очка или
при 2-х бросках есть 3 благоприятных исхода: 2,2; 1,3; 3,1 или
при 3-х бросках 3 благоприятных события: 1,1,2; 1,2,1; 2,1,1 или
при 4-х бросках 1 благоприятный исход: 1,1,1,1 дальше рассматривать смысла нет, т.к будет больше 4 очков)
Аналоги к этому заданию:
Задание 3
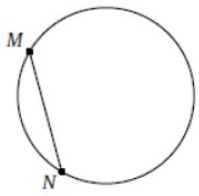
Точки M и N лежат на окружности и делят её на две дуги, одна из которых втрое короче другой. Известно, что MN=5. Найдите площадь S круга, ограниченного данной окружностью. В ответе укажите число $$\frac{S}{\pi}.$$
Ответ: 12,5
Скрыть
$$x+3x=360$$
$$x=90$$
Значит $$\angle MON=90$$ как центральный угол
Значит по теореме Пифагора $$MN=R\sqrt{2}=5$$
$$R=\frac{5}{\sqrt{2}}$$
$$S=\pi R^2=\pi\cdot\frac{25}{2}$$
Аналоги к этому заданию:
Задание 4
Найдите значение выражения $$\log_2\sqrt{\sqrt{3}-1}+\log_4(1+\sqrt{3})$$
Ответ: 0,5
Скрыть
$$0,5\log_2(\sqrt{3}-1)+0,5\log_2(1+\sqrt{3})=0,5\log_2((\sqrt{3}-1)(1+\sqrt{3}))=$$
$$=0,5\log_2(3−1)=0,5\log_2 2=0,5$$
Аналоги к этому заданию:
Задание 5
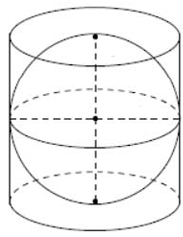
В цилиндр вписана сфера. Площадь полной поверхности цилиндра равна 42. Найдите площадь поверхности сферы.
Ответ: 28
Скрыть
$$S_{пол.пов.цилиндра}=2S_{осн}+S_{б.п.}$$
$$S_{осн}=\pi R^2$$ – окружности
$$S_{б.п.}=2\pi R\cdot2R$$ в разрезе цилиндр – это прямоугольник со сторонами: длина окружности $$(2\pi R)$$ и высотой цилиндра $$2R$$
$$S_{пол.пов.цинидра}=2\pi R^2+2\pi R\cdot2R=6\pi R^2=42$$
$$\pi R^2=7$$
$$S_{пов.сферы}=4\pi R^2=4\cdot7=28$$
Аналоги к этому заданию:
Задание 7
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием $$f = 40$$ см. Расстояние $$d_1$$ от линзы до лампочки может изменяться в пределах от 30 до 60 см, а расстояние $$d_2$$ от линзы до экрана - в пределах от 180 до 200 см. Изображение на экране будет четким, если выполнено соотношение $$\frac{1}{d_1}+\frac{1}{d_2}=\frac{1}{f}.$$ Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было чётким. Ответ выразите в сантиметрах.
Ответ: 50
Скрыть
$$\frac{1}{d_1}=\frac{1}{f}-\frac{1}{d_2}$$
Если $$d_1\rightarrow min,$$ то $$\frac{1}{f}-\frac{1}{d_2}\rightarrow max,$$ т.е. $$\frac{1}{d_2}\rightarrow min$$ тоже
Откуда $$\frac{1}{d_1}=\frac{1}{40}−\frac{1}{200}=\frac{1}{50}.$$ Значит $$d_1=50$$
Аналоги к этому заданию:
Задание 8
Проценты содержания спирта (по весу) в трех растворах образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2:3:4, то получится раствор, содержащий 32% спирта. Если же смешать их в весовом отношении 3:2:1, то получится раствор, содержащий 22% спирта. Сколько процентов спирта содержит первый раствор?
Ответ: 12
Скрыть
$$2:3:4$$ – всего 9 частей
$$3:2:1$$ – всего 6 частей
Обозначим $$b_1$$ и $$q$$ первый член геометрической прогрессии и знаменатель соответственно
Тогда из условия
$$\left\{\begin{matrix}
2b_1+3b_1q+4b_1q^2=9\cdot32\\
3b_1+2b_1q+b_1q^2=6\cdot32
\end{matrix}\right.$$
Решая систему (можно сложить и выразить сначала $$b_1$$…):
$$q=2$$ и $$b_1=12$$
Аналоги к этому заданию:
Задание 9
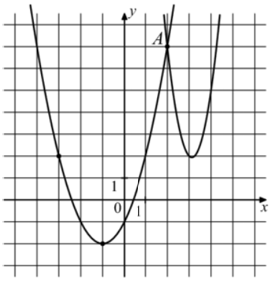
На рисунке изображены графики функций $$f(x)=4x^2-25x+41$$ и $$g(x)=ax^2+bx+c,$$ которые пересекаются в точках А и В. Найдите ординату точки В.
Ответ: 62
Скрыть
Если мысленно переместить систему координат в вершину параболы $$g(x),$$ то можно легко увидеть, что это обычная $$x^2,$$ но здесь система координат расположена по-другому, поэтому осталось понять насколько и куда сместили данную параболу, тогда
$$g(x)=(x+1)^2-2$$ (ее сместили на 1 координату влево и на 2 вниз)
Осталось найти точки пересечения
$$4x^2-25x+41=(x+1)^2−2$$
$$x^2−9x+14=0$$
$$x=2$$ – ее видно на рисунке
$$x=7$$
$$g(7)=82−2=62$$
Аналоги к этому заданию:
Задание 10
Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с вероятностью 1 - р на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен - 1?
Ответ: 0,25
Скрыть
Пусть $$x$$ - искомая вероятность
$$x=q+p\cdot x\cdot x$$
$$px^2-x+q=0$$
$$x=1$$
$$x=\frac{1-p}{p}=\frac{1-0,8}{0,8}=0,25$$
Аналоги к этому заданию:
Задание 11
Найдите точку минимума функции $$f(x)=\frac{x^3+4}{x^2}.$$
Ответ: 2
Скрыть
Найдем критические точки $$f'(x)=0$$
$$f(x)=x+\frac{4}{x^2}$$
$$f'(x)=1−\frac{8}{x^3}$$
$$x=2$$ – точка минимума по методу интервалов
$$x=0$$
Аналоги к этому заданию:
Задание 13
Точка Е лежит на боковом ребре SC правильной четырехугольной пирамиды SABCD и делит его в отношении 1:2, считая от вершины S. Через точку Е и середины сторон АВ и AD проведена плоскость $$\alpha.$$
А) Докажите, что плоскость $$\alpha$$ делит высоту пирамиды в отношении 3:2
Б) Найдите площадь сечения пирамиды SABCD плоскостью $$\alpha,$$ если сторона основания пирамиды равна 12, а высота - $$\frac{3\sqrt{6}}{2}.$$
Ответ: $$\frac{108\sqrt{7}}{5}$$
Аналоги к этому заданию:
Задание 15
Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% - проект Y. Проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y - от 29% до 34% годовых . В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможные уровни процентной ставки, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.
Ответ: 15% (см. решение 1)
Аналоги к этому заданию:
Задание 16
В треугольнике KLM биссектрисы внешних углов при вершинах К и М пересекаются в точке N. Через точки К, N и М проведена окружность с центром в точке О.
А) Докажите, что точки K, L, M и О лежат на одной окружности
Б) Найдите радиус окружности, описанной около треугольника KLM, если площадь треугольника КМО равна $$27\sqrt{3},$$ а угол KLM равен $$120^{\circ}.$$
Ответ: 6
Аналоги к этому заданию:
Задание 18
Пусть $$\overline{abc}$$ обозначает трехзначное число, равное $$100a + 10b + c,$$ где $$a, b$$ и $$c$$ - десятичные цифры, $$a\neq0.$$
А) Существуют ли такие попарно различные ненулевые десятичные цифры $$a, b$$ и $$c,$$ что $$\overline{abc} + \overline{cba} = 1595?$$
Б) Существуют ли такие попарно различные ненулевые десятичные цифры $$a, b$$ и $$c,$$ что $$3\cdot\overline{abc} = 5\cdot\overline{cba}?$$
В) Какое наибольшее значение может принимать дробь $$\frac{\overline{abc}}{\overline{cba}},$$ если среди попарно различных ненулевых десятичных цифр $$a,b$$ и $$c$$ есть цифра 6?
Ответ: А) да, Б) нет, В)$$\frac{961}{169}$$