264 вариант Алекса Ларина. Разбор ЕГЭ математика 2019.
Решаем ЕГЭ 264 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 заданий тренировочного варианта ЕГЭ Ларина №264 (alexlarin.com)
Решаем ЕГЭ 264 вариант Ларина. Подробное решение 16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №264 (alexlarin.com)
Задание 1
Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12500 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.
После вычета он получит 100-13=87% от своей зарплаты , т.е : 12500*0,87=10875 рублей.
Задание 2
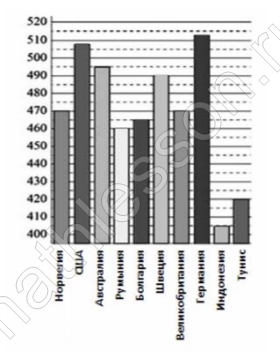
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8‐го класса по математике в 2007 году (по 1000‐бальной шкале). Найдите средний балл участников страны, занимающей третье место в данном списке.
Третье место занимает Австралия и ее средний бал 495
Задание 3
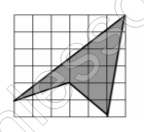
Из фанерного листа размером 60 см х 60 см нужно выпилить закрашенный многоугольник. Найдите его массу (в граммах), если известно, что плотность данной фанеры равна 0,5 г/см2.
Найдем площадь данной фигуры: $$S=60*60-\frac{1}{2} (60*50+60*10+40*10)-\frac{40+50}{2}*10=$$$$3600-2000-450=1150$$ см2
Найдем его массу: $$m=1150*0,5=575$$ грамм
Задание 4
На тренировке баскетболист Майкл попадает 3‐очковый бросок с вероятностью 0,9, если бросает мячом фирмы «Nike». Если Майкл выполняет 3‐очковый бросок мячом фирмы «Adidas», то попадает с вероятностью 0,7. В корзине лежат 10 тренировочных мячей: 6 фирмы «Nike» и 4 фирмы «Adidas». Майкл наудачу берет из корзины первый попавшийся мяч и совершает 3‐очковый бросок. Найдите вероятность того, что бросок Майкла будет точен.
Вероятность выбрать Nike и попасть им: $$P_{1}=\frac{6}{6+4}*0,9=0,54$$; выбрать Adidas и попасть им: $$P_{2}=\frac{4}{6+4}*0,7=0,28$$. Тогда вероятность вообще попасть: $$P=0,54+0,28=0,82$$
Задание 5
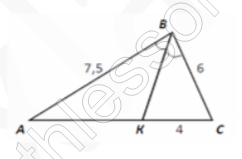
В треугольнике АВС проведена биссектриса ВК. Определите длину отрезка АК, если известно, что АВ=7,5, ВС=6, СК=4.
По свойству биссектрисы: $$\frac{BC}{AB}=\frac{KC}{AK}\Leftrightarrow$$ $$AK=\frac{AB*KC}{BC}=\frac{7,5*4}{6}=5$$
Задание 6
Движение автомобиля во время торможения описывается формулой $$S(t)=36t-5t^{2}$$ , где S – путь в метрах, t – время в секундах. Сколько секунд автомобиль будет двигаться с момента начала торможения до его полной остановки?
Производная функции расстояния есть функция скорости, найдем ее и приравняем к 0: $${S}'(t)=v(t)=36-10t\Rightarrow$$ $$v(t)=0$$ или $$t=3,6$$
Задание 7
В прямоугольном параллелепипеде ABCDA1В1C1D1 , АВ=5, AD=3, AA1=4. Найдите тангенс угла между прямыми BD1 и DC.
1) $$AD\perp AB$$ ; $$DD_{1}\perp (ABC)\Rightarrow$$ $$D_{1}A\perp AB$$ по теореме о трех перпендикулярах; $$AB\left | \right |DC$$. Тогда $$tg (BD_{1}; DC)=tg(BD_{1}, AB)=\frac{AD_{1}}{AB}$$
2) из $$\Delta AD_{1}D$$: $$AD_{1}=\sqrt{AD^{2}+AD_{1}^{2}}=5$$
3) $$tg (BD_{1}; AB)=\frac{5}{5}=1$$
Задание 8
Найдите значение выражения $$\log_{2} ^{3} (\log_{3} \sqrt[4]{3})$$
$$\log_{2}^{3}(\log_{3}\sqrt[4]{3})=$$$$\log_{2}^{3}\log_{3}3^{\frac{1}{4}}=$$$$\log_{2}^{3}\frac{1}{4}=$$$$\log_{2}^{3}2^{-2}=(-2)^{3}=-8$$
Задание 9
Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m=8 кг и радиуса R=5 см, и двух боковых с массами M=2 кг и с радиусами R+h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг*см2 , задаётся формулой $$I=\frac{(m+2M)R^{2}}{2}+M(2Rh+h^{2})$$ . При каком максимальном значении h момент инерции катушки не превышает предельного значения 1900 кг*см2? Ответ выразите в сантиметрах.
Подставим имеющееся значение : $$1900=\frac{(8+2*2)*5^{2}}{2}+2*(2*5*h+h^{2})\Leftrightarrow$$ $$3800=300+40h+4h^{2}\Leftrightarrow$$ $$4h^{2}+40h-3500=0\Leftrightarrow$$ $$h^{2}+10h-875=0$$
$$D=100+3500=3600\Leftrightarrow$$ $$h_{1}=\frac{-10+60}{2}=25$$; $$h_{2}=\frac{-10-60}{2}=-35$$
Тогда $$h_{max}=25$$, так как не может быть отрицательной
Задание 10
Три числа составляют арифметическую прогрессию. Если первые два оставить, а к третьему прибавить сумму двух первых, то полученные числа составят геометрическую прогрессию. Найдите знаменатель геометрической прогрессии.
Пусть первое число – x, третье - y, тогда по свойству арифметической прогрессии, второе: $$\frac{x+y}{2}$$
Прибавим к третьему сумму первых двух, тогда она составит : $$y+x+\frac{x+y}{2}=\frac{3(x+y)}{2}$$
Знаменатель геометрической прогрессии- отношение последующего члена к предыдущему (третьего ко второму) : $$q=\frac{3(x+y)}{2} \frac{x+y}{2}=3$$
Задание 11
Найдите точку минимума функции $$f(x)=2\sqrt[3]{x^{2}}-\frac{\sqrt[3]{x^{4}}}{4}$$
Найдем производную для данной функции : $${y}'=(2*\sqrt[3]{x^{2}}-\frac{\sqrt[3]{x^{4}}}{4})=$$$$2{(x^{\frac{2}{3}})}'-\frac{1}{4}{(x^{\frac{4}{3}})}'=$$$$2*\frac{2}{3}*x^{-\frac{1}{3}}-\frac{1}{4}*\frac{4}{3}x^{\frac{1}{3}}=0\Leftrightarrow$$$$\frac{4}{3} *\frac{1}{\sqrt[3]{x}}-\frac{1}{3}*\sqrt[3]{x}=0\Leftrightarrow$$ $$\frac{1}{3}(\frac{4}{\sqrt[3]{x}}-\sqrt[3]{x})=0\Leftrightarrow$$ $$\frac{4-\sqrt[3]{x^{2}}}{\sqrt[3]{x}}=0\Leftrightarrow$$ $$\sqrt[3]{x^{2}}=4\Leftrightarrow$$ $$x^{2}=64\Leftrightarrow$$ $$x=\pm 8$$ Тогда $$x=0$$ –точка минимума
Задание 12
А) $$2 \left | \sin x \right |+\log_{tg x}(-\frac{\left | \cos x \right |}{\sin x})=0$$
ОДЗ: $$\left\{\begin{matrix}\frac{-\left | \cos x \right |}{\sin x}>0\\tg x>0\\tg x \neq 1\\\sin x\neq 0\\\cos x\neq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\sin x<0\\\cos x<0 (1)\\tg x\neq 1\end{matrix}\right.$$
Решение с учетом ОДЗ: $$-2 \sin x+\log_{tg x}\frac{\cos x}{\sin x}=0\Leftrightarrow$$ $$-\log_{tg x}\frac{\sin x}{\cos x}=2 \sin x\Leftrightarrow$$ $$2 \sin x=-1\Leftrightarrow$$ $$\sin x=-\frac{1}{2}\Leftrightarrow$$$$\left[\begin{matrix}x=-\frac{\pi}{6}+2 \pi n \notin (1)\\x=-\frac{5\pi }{6} +2 \pi n\end{matrix}\right.$$$$n \in Z$$
Б) На промежутке: $$[-\frac{3\pi}{2};0]$$ : $$-\frac{5\pi}{6}$$
Задание 13
В правильной шестиугольной пирамиде SABCDEF сторона основания ABCDEF равна 2, а боковое ребро 3.
A) 1) Соединим AM , через M проведем прямую $$a\left | \right |AF$$; $$a\cap SD=N\Rightarrow$$ $$MN\left | \right |AF$$
2) AC-проекция AM ; Пусть SR-высота в $$\Delta ASC$$; $$SR\cap AM =K \Rightarrow$$ через K пойдет прямая , параллельная AF ( по ней пересекаются сечение и (SEB) ); пусть она пересекает SE и SB в H и G соответственно , тогда (AGMNF)-искомое сечение
3) из $$\Delta AMC$$ и точки $$S \in GM$$ по т. Менелая : $$\frac{SK}{KR}=\frac{RA}{AC}*\frac{CM}{MS}=1$$; $$\Delta SAC$$ равнобедренный $$\Rightarrow$$ $$AR=RC\Rightarrow$$ $$\frac{SK}{KR}*\frac{1}{2}*\frac{1}{1}=1\Rightarrow$$ $$\frac{SC}{KR}=\frac{2}{1}(*)$$ ( можно сразу сказать , что K-точка пересечения медиан $$\Rightarrow$$ 2: 1)
4) $$\Delta SHG\sim \Delta SEB\Rightarrow$$ $$\Delta SGK\sim \Delta SBK\Rightarrow$$ $$\frac{SK}{KR}=\frac{SC}{SB}=\frac{2}{1}$$
Б) 1) Пусть SO-высота пирамиды $$\Rightarrow$$ из $$\Delta SOB$$: $$SO=\sqrt{SB^{2}-OB^{2}}=\sqrt{5}\Rightarrow$$ $$YO=\frac{1}{3} SO=\frac{\sqrt{5}}{3}$$;
2) из $$\Delta FOA$$: $$OZ=OA*\sin A=2*\frac{\sqrt{3}}{2}=\sqrt{3}\Rightarrow$$ из $$\Delta ZOY$$: $$ZY=\sqrt{ZO^{2}+OY^{2}}=\frac{\sqrt{32}}{3}\Rightarrow$$ $$\cos YZO=\frac{ZO}{ZY}=\frac{3\sqrt{3}}{\sqrt{32}}$$
3) Пусть $$AG^{'}M^{'}N^{'}H^{'}F$$- проекция сечения на (ABC) и $$S _{AC_{1}^{'}M^{'}N^{'}H^{'}F}=S_{1}$$. Пусть S-площадь сечения $$\Rightarrow$$ $$S=\frac{S_{1}}{\cos YZO}$$
4) $$S_{ZOA}=x=\frac{1}{2} *2*2*\frac{\sqrt{3}}{2}=\sqrt{3}$$;
$$S_{AOC_{1}^{'}}=S_{ZOH^{'}}=$$$$\frac{OC_{1}^{'}}{OB}*x=$$$$\frac{SC_{1}}{SB}*x=\frac{2}{3}x=\frac{2\sqrt{3}}{3}$$
Аналогично: $$S_{G^{'}OM^{'}}=S_{H^{'}ON^{'}}=$$$$\frac{2}{3}*\frac{1}{2}x=\frac{1}{3}x$$ и $$S_{N^{'}OM^{'}}=\frac{1}{4}x$$
Тогда $$S_{1}=\sqrt{3} (1+2*\frac{2}{3}+2*\frac{1}{3}+\frac{1}{4})=\frac{13\sqrt{3}}{4}$$
$$S=\frac{13\sqrt{3}}{4} :\frac{3\sqrt{3}}{\sqrt{32}}=$$$$\frac{13\sqrt{3}*4\sqrt{2}}{4*3\sqrt{3}}=$$$$\frac{13\sqrt{2}}{3}$$
Задание 14
Решите неравенство $$\log_{\frac{1}{4}} (\sqrt{x+3}-x+3) \geq -2+\log_{\frac{1}{4}} \frac{3}{8}$$
$$\log_{\frac{1}{4}}(\sqrt{x+3}-x+3)\geq -2+\log_{\frac{1}{4}} \frac{3}{8}$$
ОДЗ: $$\left\{\begin{matrix}x+3\geq 0\\\sqrt{x+3}-x+3>0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x\geq -3\\\sqrt{x+3}>x-3 (1)\end{matrix}\right.$$
(1) :решим графически: $$x \in [-3 ; 6]$$
Решение: $$\log_{\frac{1}{4}}(\sqrt{x+3}-x+3)\geq \log_{\frac{1}{4}}16+\log_{\frac{1}{4}}\frac{3}{8}\Leftrightarrow$$
$$\log_{\frac{1}{4}}(\sqrt{x+3}-x+3)\geq \log_{\frac{1}{4}}16*\frac{3}{8}\Leftrightarrow$$ $$\sqrt{x+3}-x+3\leq 6\Leftrightarrow \sqrt{x+3}\leq x+3$$
Пусть $$\sqrt{x+3}=y\geq 0\Leftrightarrow$$ $$x+3=y^{2}$$:$$\left\{\begin{matrix}y\leq y^{2}\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}y^{2}-y\geq 0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$$$\left\{\begin{matrix}(y-1)y\geq 0\\y\geq 0\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}y\geq 0\\\left\{\begin{matrix}y\leq 0\\y\geq 0\end{matrix}\right.\end{matrix}\right. \Leftrightarrow$$ $$\left\{\begin{matrix}y=0\\y\geq 1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}\sqrt{x+3}=0\\\sqrt{x+3}\geq 1\end{matrix}\right.\Leftrightarrow$$ $$\left\{\begin{matrix}x=-3\\x\geq -2\end{matrix}\right.$$
С учетом ОДЗ : $$x \in$$ $${-3}\cup [-2 ;6)$$
Задание 15
В треугольнике АВС длина АВ равна 3, $$\angle ACB=\arcsin \frac{3}{5}$$ , хорда KN окружности, описанной около треугольника АВС, пересекает отрезки АС и ВC в точках M и L соответственно. Известно, что $$\angle ABC=\angle CML$$ , площадь четырехугольника ABLM равна 2, а длина LM равна 1.
A) $$\angle C$$ – общий ; $$\angle ABC =\angle CML\Rightarrow$$ $$\Delta ABC\sim \Delta CML$$: $$\frac{MC}{BC}=\frac{CN}{AC}=\frac{MN}{AB}=\frac{1}{3}\Rightarrow$$ $$S_{MCN}=(\frac{1}{3})^{2} S_{ABC}\Rightarrow$$ $$S_{AMNB}=\frac{8}{9}S_{ABC}\Rightarrow$$ $$S_{ABC}=\frac{9 S_{AMNB}}{8}=\frac{9}{4}$$$$\Rightarrow$$ $$S_{MCN}=\frac{1}{4}=\frac{1}{2} MN*h$$ ,где h-высота из $$C\Rightarrow h=\frac{1}{2}$$
Б) 1) Пусть O - центр описанной около $$\Delta ABC$$ окружности , тогда $$OC=OB=OA$$ - радиусы и $$OC=\frac{AB}{2 \sin ACB}=\frac{5}{2}$$
2) Пусть $$\angle ABC=\alpha \Rightarrow$$ $$\smile AC=2\alpha$$ (вписанный угол) и $$\angle LMC=\alpha$$ .
3) $$\angle LMC$$ - угол между хордами AC и KN $$\Rightarrow$$ $$\frac{\smile AK+\smile CN}{2}=\alpha \Rightarrow$$ $$\smile AK+\smile CN=2\alpha$$. При этом $$\smile AC=\smile AK+\smile KC=2\alpha \Rightarrow$$ $$\smile CN=\smile KC\Rightarrow$$ $$KC=CN$$
4) Пусть $$OC\cap KN=D\Rightarrow$$ $$CD=h=\frac{1}{2}$$( расстояние от C до ML ) $$\Rightarrow$$ $$OD=OC-DC=\frac{5}{2}-\frac{1}{2}=2\Rightarrow$$ $$KD=\sqrt{OK^{2}-OD^{2}}=1,5\Rightarrow$$ $$KN=3\Rightarrow$$ $$S_{KCN}=\frac{1}{2}*CD*KN=\frac{3}{4}$$
Задание 16
На счет, который вкладчик имел в начале первого квартала, начисляется в конце этого квартала r1 процентов, а на тот счет, который вкладчик имел в конце второго квартала, начисляется в конце этого квартала r2 процентов, причем r1+r2=150 . Вкладчик положил на счет в начале первого квартала некоторую сумму и снял в конце того же квартала половину этой суммы. При каком значении r1 счет вкладчика в конце второго квартала окажется максимально возможным?
Пусть S-первоначальная сумма вклада, тогда после первого начисления на счете $$S(1+\frac{r_{1}}{100})$$, а после снятия половины первоначального вклада: $$S(1+\frac{r_{1}}{100})-\frac{S}{2}$$. Учтем, что $$r_{2}=150-r_{1}$$.
После второго начисления на счету : $$(S(1+\frac{r_{1}}{100})-\frac{S}{2})(1+\frac{150-r_{1}}{100})=S(r_{1})$$
Необходимо найти точку максимума: $$S^{'}(r_{1})=(S(\frac{1}{2}+\frac{r_{1}}{100})(\frac{250-r_{1}}{100}))^{'}=$$$$(S(\frac{50+r_{1}}{200})(\frac{250-r_{1}}{100}))^{'}$$
При этом максимум $$S(r_{1})$$ совпадает с максимумом $$K(r_{1})=(50+r_{1})(250-r_{1})$$
$$K^{'}(r_{1})=(250-r_{1})-(50+r_{1})=0\Leftrightarrow$$ $$200-2r_{1}=0\Leftrightarrow$$ $$r_{1}=100$$
Задание 17
При каких значениях параметра a неравенство $$\log_{\frac{-2a-13}{5}} (\frac{\sin x -\sqrt{3}\cos x -a-4}{5})>0$$ выполняется для любых значений x ?
Пусть $$m(x) =\sin x-\sqrt{3}\cos x$$, тогда $$m^{'}(x)=\cos x+\sqrt{3}\sin x=0\Leftrightarrow$$ $$\sqrt{3}tg x=-1\Leftrightarrow$$ $$x=-\frac{\pi}{6}+\pi n , n \in Z$$
$$m(-\frac{\pi}{6})=\sin -\frac{\pi}{6}-\sqrt{3}\cos -\frac{\pi}{6}=-\frac{1}{2}-\frac{3}{2}=-2\rightarrow m_{min}$$
$$m(\frac{5\pi}{6})=\sin \frac{5 \pi}{6}-\sqrt{3} \cos \frac{5 \pi}{6}=2\rightarrow m_{max}$$
Получим систему:
$$\left\{\begin{matrix}(\frac{-2a-13}{5}-1)(\frac{m-a-4}{5}-1)>0(4)\\\frac{-2a-13}{5}>0(1)\\\frac{m-a-4}{5}>0(3)\\\frac{-2a-13}{5}\neq 1(2)\end{matrix}\right.$$
$$ (1): -2a-13>0\Leftrightarrow a<-6,5$$
$$(2): -2a-13\neq 5\Leftrightarrow a\neq -9$$
$$(3) :a<-6,5 , -a-4>2,5 \Rightarrow \frac{m-a-4}{5}>0$$ при любом m( и ,следовательно, x)
$$(4) :(-2a-18)(m-a-9)>0\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}-2a-18>0\\m-a-9>0\end{matrix}\right. \\\left\{\begin{matrix}-2a-18<0\\m-a-9<0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow$$ $$\left[\begin{matrix}\left\{\begin{matrix}x<-9\\m-a-9>0\end{matrix}\right. (5)\\\left\{\begin{matrix}x>-9\\m-a-9<0\end{matrix}\right.(6)\end{matrix}\right.$$
$$(5)$$: при $$a<-9$$: $$-a-9>0$$ при любом a , следовательно, чтобы было решение для любого m должно выполняться: $$m_{min}-a-9>0\Leftrightarrow$$ $$-2-a-9>0\Leftrightarrow$$ $$a<-11$$. Получим $$a \in (-\infty ;-11)$$
$$(6)$$ : аналогично $$m_{max}-a-9<0\Rightarrow$$ $$2-a-9<0\Rightarrow a>-7$$. Получим $$a \in (-7; +\infty )$$
С учетом (1): $$a \in (-\infty ;-11)\cup (-7;-6,5)$$
Задание 18
Задано число от 1 до n. За один ход можно выбрать произвольное подмножество множества чисел от 1 до n и спросить, принадлежит ли ему заданное число. При ответе «да» будет начислено a баллов, при ответе «нет» – b баллов.