335 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

В иностранном отделе библиотеки имеются книги на английском, французском и немецком языках. Английские книги составляют 36% всех книг, французские‐75% английских, а остальные 222 книг немецкие. Сколько всего иностранных книг в библиотеке?

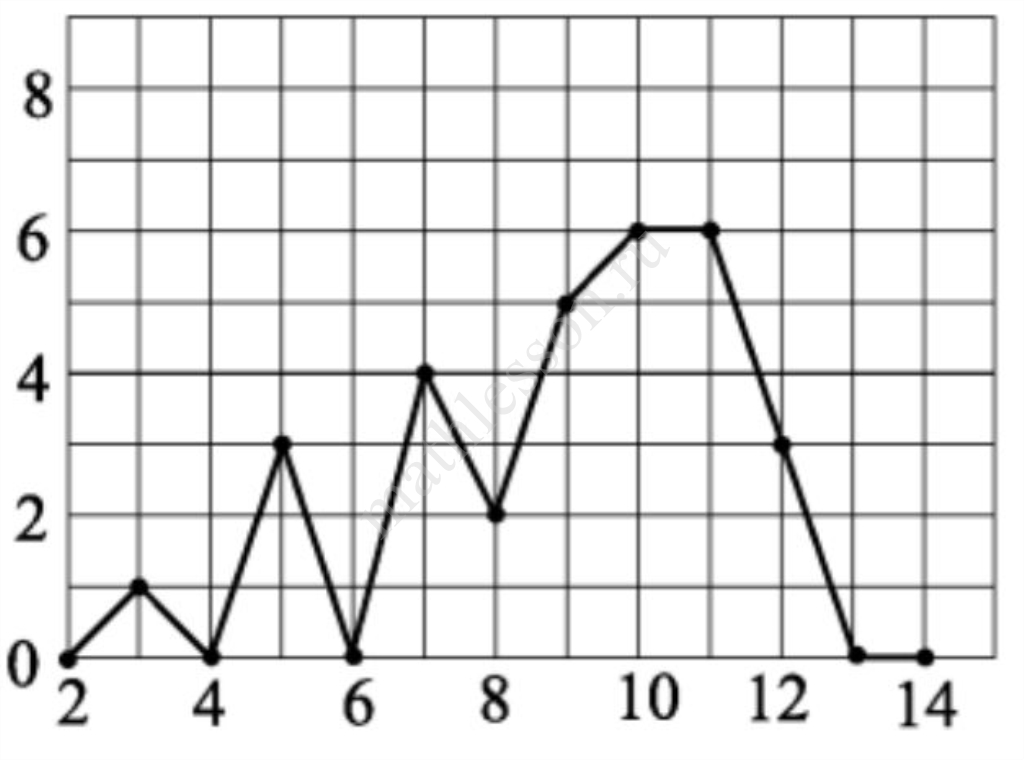
На рисунке жирными точками показано суточное количество осадков, выпавших в Дождегорске со 2 по 14 марта 2020 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало 4 мм осадков?

Найдите тангенс угла KST (cм. рис.)

При включении зажигания двигатель начнет работать с вероятностью 0,6. Найдите вероятность того, что для запуска двигателя придется включать зажигание не более трех раз.

Решите уравнение: $$2^{\sqrt{x+1}}=16\sqrt{0,25^{5-\frac{x}{4}}}$$. Если уравнение имеет несколько корней, то в ответе укажите меньший из корней.

В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5. Определите площадь треугольника.

Движение двух материальных точек вдоль одной прямой заданы уравнениями $$S_{1}=4t^{2}+2$$, $$S_{2}=3t^{2}+4t-1$$, ( $$S_{1},S_{2}$$–пройденный путь в метрах, t ‐ время в секундах). Найдите скорости движения точек в те моменты, когда пройденные ими расстояния равны. В ответе укажите сумму всех полученных значений скоростей.

Основанием пирамиды служит треугольник со сторонами 6, 10 и 14. Каждое из боковых рёбер пирамиды наклонено к основанию под углом 45^о. Вычислите объём пирамиды.

Вычислите $$\log_{\sqrt{3}}\sqrt[6]{a}$$, если $$\log_{a} 27=10$$.

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону $$U=U_{0}\sin (\omega t+\phi)$$, где t – время в секундах, амплитуда $$U_{0}=10$$В, частота $$\omega=150^{\circ}$$\c, фаза $$\phi=30^{\circ}$$. Датчик устроен так, что если напряжение в нем не ниже чем 5 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Пчёлы, перерабатывая цветочный нектар в мёд, освобождают его от значительной части воды. Исследования показали, что нектар содержит 70 % воды, а полученный из него мёд – 16 % воды. Сколько килограммов нектара приходится перерабатывать пчёлам для получения 1 кг мёда?

Найдите наименьшее значение функции $$y=x+\cos^{2}x$$ на отрезке $$[0;\frac{\pi}{2}]$$

Основание АВС правильной треугольной пирамиды SABC вписано в нижнее основание цилиндра, а вершина S расположена на оси О₁О₂цилиндра (точка О₁– центр верхнего основания). Объем цилиндра равен $$21\pi$$, а объем пирамиды 33 .

Решите неравенство: $$|\log_{x+1}\sqrt{(x-2)^{2}}+2|\geq -3+\log_{\frac{1}{x+1}}\sqrt{(x-2)^{6}}$$

Отрезки AK, BL, CN – высоты остроугольного треугольника АВС. Точки Р и Q – проекции точки N на стороны АС и ВС соответственно.

Необходимо произвести отделку здания, имеющего форму прямоугольного параллелепипеда, объемом 432 м³. Отделка стены здания, примыкающей к внутреннему строению, обходится в 1000 руб. за квадратный метр. Отделка трех фасадных стен обходится в 2000 руб. за квадратный метр. А заливка крыши, форма которой является квадратом, обходится в 7000 руб. за квадратный метр. Найдите размеры здания, отделочные работы которого при данных условиях являются наименьшими по стоимости.

Найдите все значения параметра а, при которых неравенство $$\cos x-2\sqrt{x^{2}+9}\leq -\frac{x^{2}+9}{a+\cos x}-a$$ имеет единственное решение.

Имеется m одинаковых шоколадок, которые можно разделить поровну на n школьников. Каждую шоколадку разрешается разломить не более одного раза (необязательно на равные части).