333 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

Рейтинг одного из кандидатов в президенты по предварительным данным агентства "Альфа" составил 37%. Рейтинг того же кандидата по предварительным данным агентства "Омега" составил в 33,3 раза меньше официально объявленного после выборов результата. Каков был рейтинг кандидата по данным "Омеги", если результат превзошёл ожидания "Альфы" на 170% от предварительной оценки?

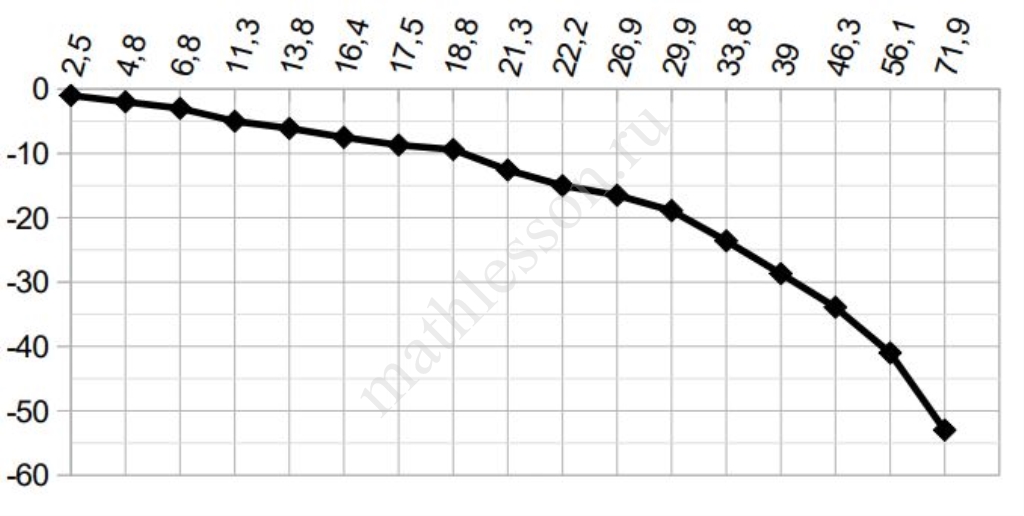
На графике показана зависимость температуры замерзания смеси воды с этанолом (по оси ординат) от массовой доли этанола в процентах(по оси абсцисс). Шофёр везёт в деревню 4 кг чистого спирта в канистре. Определите по графику, сколько килограмм спирта останется в канистре, если часть его уйдёт на изготовление трёх литров стеклоомывающей жидкости, не замерзающей до температуры ‐15 градусов? Вес 1 л жидкости принять за 1 кг, результат округлить до сотых

Площадь каждого большого треугольника на рисунке составляет 594. Найдите площадь круга, делённую на $$\pi$$.

Подбросили два игральных кубика. Найдите вероятность того, что сумма выпавших очков будет простым числом. Результат округлите до сотых.

Решите уравнение $$\log_{6}(x^{2}-x)=\log_{x+3}(x+3)$$. Если уравнение имеет более одного корня, в ответе укажите наименьший из них.

Квадрат площадью 666 и ромб с углом 30^o имеют равные стороны. Найдите площадь ромба.

На рисунке показан график функции $$f(x)$$. Найдите на отрезке [‐15; 17] наименьшую длину промежутка, на котором совпадают знаки функции $$g(x)=f(x)+333$$ и её производной.

Площадь полной поверхности треугольной пирамиды ABCD равна 333 см². Найдите площадь полной поверхности треугольной пирамиды, каждое ребро которой в 3 раза меньше, чем у пирамиды ABCD. Ответ дайте в см².

Найдите значение выражения $$\frac{-333\sin 333^{\circ}}{\sin 27^{\circ}}$$

Масса радиоактивного вещества оценивается по формуле $$m=m_{0}\cdot 2^{-\frac{t}{T}}$$ , где m₀, t, T ‐ начальная масса вещества, время, прошедшее от начала, и период полураспада соответственно. При измерении периода полураспада радиоактивного изотопа мышьяка 81 $$As_{81}^{33}$$ его масса уменьшилась до 0,125 от начальной за 99,9 сек. За какое время в смеси 1:1 $$As_{81}^{33}$$ и стабильного изотопа мышьяка соотношение станет равным 1:2? ( в стабильный изотоп мышьяка при распаде не переходит)

Поезда проезжают платформу "Встреча" в направлении с севера на юг и с юга на север. Интервал между поездами одного направления составляет 20 минут. Когда Отелло приехал на станцию поездом с юга, до прибытия первого поезда с севера оставалось 13 минут. Однако Отелло заметил, что начиная с третьего прибывшего с севера поезда, интервал между поездами сокращается на 1 минуту. Сколько поездов с севера встретил на платформе "Встреча" Отелло прежде, чем задушил Дездемону, приехавшую через 3 часа и 33 минуты после него поездом с севера на юг?

Найдите сумму значений функции $$y=4\cos^{3}x-3\cos x$$ в точках экстремума принадлежащих промежутку $$[0;11\pi)$$.

Боковое ребро правильной четырехугольной пирамиды SABCD (S – вершина , BD – диагональ основания) образует угол 45^о c плоскостью основания, а сторона равна 4. Через среднюю линию треугольника ABD, не пересекающую BD и середину высоты пирамиды, проведена плоскость $$\alpha$$.

Решите неравенство: $$333^{3}+3x^{2}\cdot 333+3^{\log_{x}(x-333)}\geq x^{3}+3^{3}\cdot x\cdot 12321$$

Три точки А, В и С разбивают окружность на три дуги. Каждая из дуг разбивается на три равные части так, что на окружности последовательно стоят точки А, А₁, А₂, В, В₁, В₂, С, С₁, С₂.

А) Докажите, что точки пересечения прямых А₁В₂, В₁С₂ и С₁А₂образуют равносторонний треугольник

Б) Найдите стороны этого треугольника, если АС=1, ВС=2, АВ= 3

В 33‐ем году нашей эры в Иерусалимском банке был открыт вклад на 33 серебренника под 10% вековых. В пятом веке сразу после начисления процентов из‐за нестабильной политической обстановки Иерусалимский банк вводит ежегодную пошлину на хранение любого вклада, зафиксировав размер пошлины как 0,1% от величины вклада на момент введения пошлины. В 15 веке сразу после начисления процентов за вычетом пошлины из‐за девальвации (обесценивания) серебренника пошлину отменили, а вклад конвертировали (перевели) в золото по ставке 10 серебренников за один золотой, округлив получившееся число золотых до ближайшего целого. Процентную ставку для золотых повысили до 20% вековых, однако первое начисление состоялось только век спустя после конвертации (перевода). Сколько золотых удалось снять со счёта при его закрытии из‐за Первой Мировой войны 1914‐1918 годов 20 века?

Найдите все значения параметра a , при каждом из которых система уравнений $$\left\{\begin{matrix} 3^{3}+3a=3x^{3}(x+3)+3x^{2}-3x^{3}+(a+3)(y+3+x)(y+3-x)\\3=y+\sqrt{3(1-3y-x)-3y+x(1-x)} \end{matrix}\right.$$ имеет ровно три решения.

На асфальте мелом написали в ряд 333 цифры 3 и расставили между некоторыми из них знаки «плюс» и «минус».