364 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.
Решаем ЕГЭ 364 вариант Ларина ЕГЭ 2022 по математике. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №364 (alexlarin.com)
Больше разборов на моем ютуб-канале
Аналоги к этому заданию:
Задание 1
Решите уравнение $$5^{x^2-3}\cdot6^x.$$ В ответе укажите наибольший корень этого уравнения.
Ответ: 2
Скрыть
$$180=5\cdot6^2$$
$$5x{^2-3}\cdot6^x=5\cdot6^2$$
Откуда вытекает, что
$$x^2-3=1$$
$$x=2$$
Это система, значит единственный корень $$x=2$$
Аналоги к этому заданию:
Задание 2
Пятеро друзей-автолюбителей взяли автомобиль в аренду для путешествия. С помощью жребия они выбирают двоих, которые в первый день будут поочередно водителями. Какова вероятность того, что М., входящий в состав группы, будет водителем в первый день путешествия?
Ответ: 0,4
Скрыть
Классическая вероятность $$P(A)=\frac{m}{n},$$ где $$m$$ – количество благоприятных исходов, а $$n$$ – всего исходов
В нашем случае $$m=2, n=5$$
Значит $$P(A)=\frac{2}{5}=0,4$$
Аналоги к этому заданию:
Задание 3
В треугольнике АВС угол С равен $$90^{\circ}, \cos\angle B =\frac{\sqrt{51}}{10}.$$ Найдите синус внешнего угла при вершине В.
Ответ: 0,7
Скрыть
$$\sin\angle B=\pm\sqrt{1−\frac{51}{100}}=\pm\frac{7}{10}$$
Но так как треугольник прямоугольный, то углы ∠B и ∠C – острые, значит знак можно поставить однозначно
$$\sin\angle B=\frac{7}{10}$$
$$\sin(внешнего\, при\, B)=\sin(180-\angle B)=\sin\angle B=\frac{7}{10}=0,7$$
Аналоги к этому заданию:
Задание 4
Найдите значение выражения $$\frac{\sin^2 20^{\circ}+\sin^2 70^{\circ}}{2\sin(180^{\circ}+\alpha)},$$ если $$\sin\alpha=\frac{1}{3}$$
Ответ: -1,5
Скрыть
$$\sin^2 20^{\circ}+\sin^2 70^{\circ}=\sin^2 20^{\circ}+\sin^2(90^{\circ}-20^{\circ})=\sin^2 20^{\circ}+\cos^2 20^{\circ}=1$$
$$\sin(180^{\circ}+\alpha)=-\sin\alpha$$
$$\frac{1}{-\frac{2}{3}}=-1,5$$
Аналоги к этому заданию:
Задание 5
Сосуд в виде правильной треугольной пирамиды высотой $$25\sqrt{3}$$ см доверху заполнен водой. Найдите, на какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, имеющий форму куба со стороной, равной стороне основания данной треугольной пирамиды. Ответ выразите в сантиметрах.
Ответ: 6,25
Скрыть
Пусть сторона основания пирамиды $$a$$
Тогда
$$V_{пир}=\frac{1}{3}\cdot S_{осн}\cdot 25\sqrt{3}$$
$$S_{осн}=\frac{a^2\sqrt{3}}{4}$$ – т.к. треугольник правильный
Потом переливаем всю воду в куб, запишем равенство объемов
$$a^3=\frac{1}{3}\cdot\frac{a^2\sqrt{3}}{4}\cdot25\sqrt{3}$$
Откуда $$a=\frac{25}{4}=6,25$$ - это и есть высота кубика
Аналоги к этому заданию:
Задание 6
Функция $$y=f(x)$$ определена на промежутке (- 4; 4). На рисунке изображен ее график и касательная к этому графику в точке с абсциссой $$x_0 = -3.$$ Вычислите значение производной функции $$y=\frac{x}{4}\cdot f(x)+5x$$ в точке $$x_0 = -3.$$
Ответ: 5,125
Скрыть
$$y'=\frac{1}{4}f(x)+\frac{x}{4}f'(x)+5$$
Из рисунка видно, что $$f(-3)=-1$$
По геометрическому смыслу производной
$$\tg(180-\alpha)=-\tg\alpha=-\frac{1}{2}=f'(x_0)$$
Подставляя все, получаем $$y'(-3)=5,125$$
Аналоги к этому заданию:
Задание 7
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением $$pV^{1,2} = const,$$ где $$p$$ (атм.)— давление в газе, $$V$$ — объем газа в литрах. Изначально объем газа равен 51,2 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 64 атмосфер. Определите, до какого минимального объёма можно сжать газ. Ответ выразите в литрах.
Ответ: 1,6
Аналоги к этому заданию:
Задание 8
Экипаж дальнобойщиков проехал расстояние 6375 км с определенной скоростью без остановок. На обратном пути водители планируют сделать остановку на 10 часов для отдыха. Для этого на обратном пути им необходимо увеличить скорость на 10 км/ч по сравнению с прямым маршрутом. Найдите (в км/ч) значение первоначальной скорости, если на путь в обоих направлениях затрачено одинаковое количество времени.
Ответ: 75
Скрыть
$$6375=Vt_1$$
$$6375=(V+10)t_2$$
Выражаем время из каждого уравнения
По условию
$$\frac{6375}{V}+10=\frac{6375}{V+10}$$
$$V=75$$
Аналоги к этому заданию:
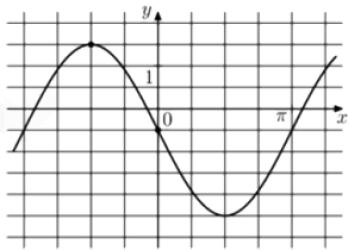
Задание 9
Ответ: -4
Скрыть
На рисунке уже отмечены точки, которые легче всего взять
$$\left\{\begin{matrix} 3=a\cdot\sin\frac{-\pi}{2}+b\\ -1=a\cdot\sin0+b \end{matrix}\right.$$
Решая систему, получаем ответ -4
Аналоги к этому заданию:
Задание 10
Артем бросил одновременно две игральных кости, ни на одной из них не выпало шесть. Какова вероятность при этом условии, что в сумме выпало 9 очков?
Ответ: 0,08
Скрыть
Задача на условную вероятность
$$P(B|A)=\frac{P(AB)}{P(A)}$$
$$A$$ – не выпало ни на одной 6
$$B$$ – выпало в сумме 9
$$P(A)=\frac{25}{36}$$
$$P(AB)=\frac{2}{36}$$
$$P(B|A)=\frac{2}{25}=0,08$$
Аналоги к этому заданию:
Задание 11
Найдите наибольшее значение функции $$y=\frac{15\sqrt{3}}{\pi}+\frac{3}{\pi}\cdot (24x-5\tg x)$$ на отрезке $$[-\frac{\pi}{6};\frac{\pi}{3}]$$
Ответ: 24
Скрыть
Найдем критические точки
$$y'=0$$
$$\frac{3}{\pi}\cdot\frac{24\cos^2 x-5}{\cos^2 x}$$
$$\cos x=-\frac{\sqrt{5}}{\sqrt{24}}$$ точно нам не подходит, т.к. решение не будет в нужном отрезке
$$\cos x=\frac{\sqrt{5}}{\sqrt{24}}$$ – тоже скорее всего не подходит, разберемся почему
$$\sqrt{\frac{5}{24}}=\frac{\sqrt{30}}{12}<\frac{6}{12}<\frac{1}{2}$$
$$\cos\frac{\pi}{3}=0,5$$
Т.е. получаем, что точки из решения $$\cos x=\frac{\sqrt{5}}{\sqrt{24}}$$ тоже не попадут в отрезок
Значит, осталось проверить только граничные точки.
$$y(\frac{\pi}{3})=\frac{15\sqrt{3}}{\pi}+\frac{3}{\pi}(24\cdot\frac{\pi}{3}-5\tg\frac{\pi}{3})=\frac{15\sqrt{3}}{\pi}+24-\frac{15\sqrt{3}}{\pi}=24.$$
Аналоги к этому заданию:
Задание 13
В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 4, боковые ребра равны 6. Точка М - середина ребра СС1, на ребре BB1 отмечена точка N, такая, что BN : NB1 = 1 : 2.
а) Докажите, что плоскость AMN делит ребро DD1 в отношении 1 : 5, считая от точки D.
б) Найдите угол между плоскостями АВС и AMN.
Ответ: $$\arctg\frac{\sqrt{5}}{4}$$
Аналоги к этому заданию:
Задание 15
Строительство нового завода стоит 140 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны $$0,2x^2 + 3x +1$$ млн рублей в год. Если продукцию завода продать по цене $$p$$ тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит $$px-(0,2x^2 + 3x +1).$$ Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки завода цена на продукцию $$p = 7$$ тыс. руб. за единицу. Каждый последующий год цена увеличивается на 2 тыс. руб. за единицу. За сколько лет окупится строительство завода?
Ответ: 3
Аналоги к этому заданию:
Задание 16
В остроугольном треугольнике АВС проведены высоты ВВ1 и СС1. Прямые В1С1 и ВС пересекаются в точке Р.
a) Докажите, что треугольники РВС1 и РВ1С подобны.
б) Найдите расстояние от вершины А до точки пересечения высот треугольника АВС, если $$ВР = ВB_1, \angle АВС = 80^{\circ}, ВС = 2\sqrt{3},$$ а точка В лежит между С и Р.
Ответ: 6
Аналоги к этому заданию:
Задание 18
Вова задумал натуральное число $$a$$ и посчитал сумму его цифр, эту сумму он обозначил $$b.$$ Затем он посчитал сумму цифр числа $$b$$ и обозначил ее через $$c.$$ Оказалось, что среди чисел $$a, b$$ и $$c$$ нет одинаковых.
а) Может ли $$a + b + c = 3000?$$
б) Может ли $$a + b + c = 2000?$$
в) Сколько существует четырехзначных чисел $$a,$$ для которых $$c = 4?$$
Ответ: А) да, Б) нет, В) 980