390 вариант Алекса Ларина. Разбор ЕГЭ математика 2022.

$$3^{\log_9(5x-5)}=5$$

$$(5x-5)^{\log_9 3}=5$$

$$5x-5>0$$

$$(5x-5)^{\frac{1}{2}}=5$$

$$5x-5=25$$

$$x=6$$

Вероятность того, что студент не ответит на первый вопрос $$1 - 0,9 = 0,1$$

Вероятность того, что студент не ответит на второй вопрос $$1 - 0,8 = 0,2$$

Вероятность того, что студент не ответит на третий вопрос $$1-0,7=0,3$$

Вероятность того, что студент ответит не менее, чем на два вопроса равна сумме вероятностей того, что он ответит на все вопросы правильно, ответит на первый и второй правильно и не ответит на третий, ответит на первый и третий правильно и не ответит на второй, ответит на второй и третий правильно и не ответит на первый:

$$P(A)=0,9\cdot0,8\cdot0,7+0,9\cdot0,8\cdot0,3+0,9\cdot0,2\cdot0,7+0,1\cdot0,8\cdot0,7=0,902$$

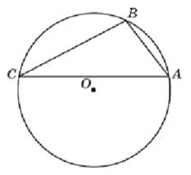
Угол ABC является вписанным углом, который равен половине градусной меры большей дуги AC, на которую он опирается. Пусть x – градусная мера условной единицы, тогда можно записать, что

$$1x+3x+5x=360^{\circ}$$

откуда

$$9x=360^{\circ}$$

$$x=40^{\circ}$$

То есть, дуга $$AC=40^{\circ},$$ дуга $$BA=3\cdot40=120^{\circ},$$ а дуга $$AC=5\cdot40=200^{\circ}.$$ Следовательно, угол ABC, равен:

$$\angle ABC=\frac{AC}{2}=\frac{200^{\circ}}{2}=100^{\circ}$$.

$$\frac{\sqrt[24]{12}\cdot\sqrt[12]{12}}{\sqrt[8]{12}}=\frac{12^{\frac{1}{24}}\cdot12^{\frac{1}{12}}}{12^{\frac{1}{8}}}=12^{\frac{1}{24}+\frac{1}{12}-\frac{1}{8}}=12^0=1$$

Пусть $$а$$ – сторона правильного треугольника (лежащего в основание правильной треугольной призмы). $$R$$ – радиус основания цилиндра.

$$R = \frac{a}{\sqrt{3}}\Rightarrow a=R\sqrt{3}=2\sqrt{3}\cdot\sqrt{3}=6$$

Площадь одной боковой грани:

$$S = 6\cdot5 = 30$$

Площадь боковой поверхности:

$$S_{бок} = 3\cdot S = 90$$

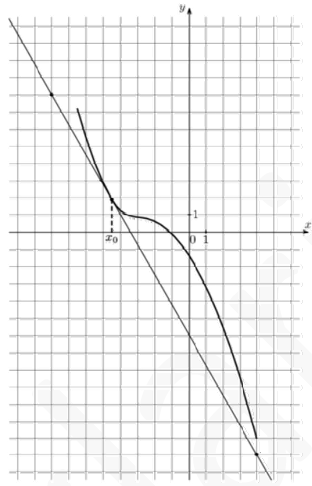
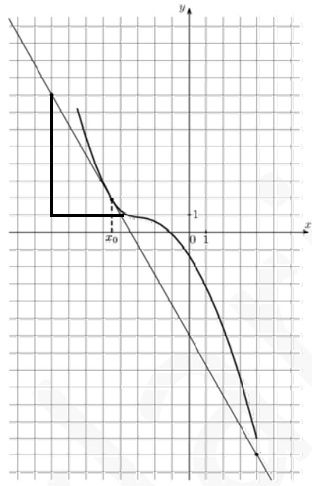
Значение производной равно тангенсу угла между касательной и осью Ox.

Достроим прямоугольный треугольник как на рисунке.

Получим тангенс, равный $$\frac{7}{4}.$$ При этом функция убывает, значит $$f'(x)<0\Rightarrow f'(x)=-\frac{7}{4}=-1,75$$

$$16,2=0,9\cdot3\cdot10^{-6}\cdot3\cdot10^6\cdot\log_2\frac{36}{U}$$

                    $$0,9\cdot3\cdot3=0,9\cdot9=8,1$$

$$16,2=8,1\cdot\log_2\frac{36}{U}$$

$$\log_2\frac{36}{U}=\frac{16,2}{8,1}$$

$$\log_2\frac{36}{U}=2$$

$$\frac{36}{U}=2^2$$

$$36=4U$$

$$U=\frac{36}{4}=9$$

Скорость обгона пассажирским поездом товарного составляет $$100-80=20$$ км/ч. Товарный поезд имеет длину 2100 метров или 2,1 км. В задаче сказано, что пассажирский поезд прошел мимо товарного за 7,5 минут (за $$\frac{7,5}{60}$$ часа) со скоростью 20 км/ч. То есть была пройдена вся длина товарного поезда и еще длина самого пассажирского поезда. Обозначим через $$x$$ длину пассажирского поезда, тогда расстояние равное $$x+2,1$$ было пройдено за $$\frac{7,5}{60}=\frac{1}{8}$$ часа со скоростью 20 км/ч. Получаем уравнение

$$(x+2,1):\frac{1}{8}=20$$

$$(x+2,1)\cdot8=20$$

$$8x+16,8=20$$

$$8x=3,2$$

$$x=\frac{3,2}{8}=0,4$$

То есть длина пассажирского поезда равна 0,4 км или 400 метров.

График проходит через $$(1;-1); (3;1); (5;-5).$$ Получим:

$$\left\{\begin{matrix} -1=\frac{a\cdot1+b}{1+c}\\ 1=\frac{3a+b}{3+c}\\ -5=\frac{5a+b}{5+c} \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -1-c=a+b\\ 3+c=3a+b\\ -25-5c=5a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 4+2c=2a\\ 28+6c=-2a\\ 3+c=3a+b \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 32+8c=0\\ a=2+c\\ b=c+3-3a \end{matrix}\right.\Leftrightarrow$$

$$\Leftrightarrow\left\{\begin{matrix} c=-4\\ a=-2\\ b=5 \end{matrix}\right.$$

Получим: $$y=\frac{-2x+5}{x-4}.$$ Тогда $$f(29)=\frac{-2\cdot29+5}{29-4}=\frac{-53}{25}=-2,12$$

Предположим, что бросали первый кубик. Тогда вероятность того, что в каком-то порядке выпали 3 и 5 очков, равна $$\frac{1}{6}\cdot\frac{1}{6}+\frac{1}{6}\frac{1}{6}=\frac{1}{18}.$$ Теперь предположим, что бросали второй кубик. Поскольку на втором кубике числа 3 и 5 встречаются по два раза, вероятность того, что в каком-то порядке выпали 3 и 5 очков, равна $$\frac{2}{6}\cdot\frac{2}{6}+\frac{2}{6}\cdot\frac{2}{6}=\frac{2}{9}.$$ Таким образом, искомая вероятность равна:

$$\frac{\frac{2}{9}}{\frac{1}{18}+\frac{2}{9}}=\frac{4}{1+4}=0,8$$

$$f'(x)=\frac{-5\cdot(x-2)-(14-5x)\cdot1}{(x-2)^2}=\frac{-5x+10-14+5x}{(x-2)^2}=\frac{-4}{(x-2)^2}$$

$$\frac{-4}{(x-2)^2}=0$$

$$x\notin\varnothing\Rightarrow$$ нет точек экстремума.

Значит, функция достигает max и min либо в -3, либо в 1

$$f(-3)=\frac{14-5\cdot(-3)}{-3-2}=\frac{14+15}{-5}=\frac{29}{-5}=-5,8$$

$$f(1)=\frac{14-5}{1-2}=-9$$

$$f(1)<f(-3)\Rightarrow -9$$ - наименьшее значение