323 вариант Алекса Ларина. Разбор ЕГЭ математика 2021.

Решаем ЕГЭ 323 вариант Ларина ЕГЭ 2021 по математике. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12, 13,14,15,16,17,18,19 заданий тренировочного варианта ЕГЭ Ларина №323 (alexlarin.com)

Аналоги к этому заданию:

Задание 1

В течение года произошло три понижения цены товара, причем на 30% каждый раз. Найти конечную цену товара, если первоначально он стоил 100000 рублей.

Ответ: 34300

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть После понижения цены на $$30\%$$ товар стоит $$70\%$$ от предыдущей цены, т.е. $$\left(\left({10}^5\cdot 0,7\right)\cdot 0,7\right)\cdot 0,7=34300$$.

Аналоги к этому заданию:

Задание 2

На графике изображена зависимость крутящего момента двигателя катера от числа его оборотов. На оси абсцисс откладывается число оборотов двигателя в минуту, на оси ординат - крутящий момент в Н•м. Скорость этого катера, измеренная в км/ч, выражается формулой $$v=0,04n$$, где $$n$$ - число оборотов двигателя в минуту. Какую наименьшую скорость (в км/ч) должен иметь катер, чтобы крутящий момент его двигателя был не меньше 60 Н•м?

Ответ: 30

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть Крутящий в 60 Н•м достигается впервые при 750 об/мин. Тогда скорость: $$V=0,04\cdot 750=30$$ км/ч.

Аналоги к этому заданию:

Задание 3

Сторона квадрата АВCD равна 6. Найдите скалярное произведение векторов $$\overline{AB}$$ и $$\overline{AC}$$.

Ответ: 36

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\overline{AB}\cdot \overline{AC}=\left|\overline{AB}\right|\cdot \left|\overline{AC}\right|\cdot {\cos \alpha \ }$$, где $$\alpha $$ - угол между $$AB$$ и $$AC$$, т.е. $$45{}^\circ $$.

При этом $$\left|\overline{AC}\right|=\sqrt{AB^2+BC^2}=6\sqrt{2}\to \overline{AB}\cdot \overline{AC}=6\cdot 6\sqrt{2}\cdot \frac{\sqrt{2}}{2}=36$$

Аналоги к этому заданию:

Задание 4

Павел Иванович регистрирует автомобиль и получает новый трехзначный номер. Все три цифры нового номера случайны (номер 000 не разрешен). Найдите вероятность того, что при случайном выборе в новом номере все три цифры будут одинаковы. Результат округлить до тысячных.

Ответ: 0,009

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Всего номеров $$999-0=999=N$$. Три цифры одинаковы в $$n=9$$ номерах $$(111,222,\dots ,999)$$.

Тогда вероятность: $$P\left(A\right)=\frac{n}{N}=\frac{1}{111}=0,(009)\approx 0,009$$

Аналоги к этому заданию:

Задание 5

Решите уравнение $$\left(x+4\right)\left(x+1\right)-3\sqrt{x^2+5x+2}=6$$. Если уравнение имеет несколько корней, то в ответ запишите наибольший из них.

Ответ: 2

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\left(x+4\right)\left(x+1\right)-3\sqrt{x^2+5x+2}=6$$.

Пусть $$\sqrt{x^2+5x+2}=y$$, тогда $$\left(x+4\right)\left(x+1\right)=x^2+5x+4=y^2+2$$.

Получим: $$y^2+2-3y=6\leftrightarrow y^2-3y-4=0\leftrightarrow$$$$ \left[ \begin{array}{c} y_1=-1 \\ y_2=4 \end{array} \right.$$;

$$y\ge 0\to y=4:\ \sqrt{x^2+5x+2}=4\leftrightarrow$$$$ x^2+5x-14=0\to$$$$ \left[ \begin{array}{c} x_1=-7 \\ x_2=2 \end{array} \right.$$. Ответ: 2.

Аналоги к этому заданию:

Задание 6

Угол при вершине равнобедренного треугольника равен $$120{}^\circ $$. Боковая сторона равна 4. Найдите квадрат длины медианы, проведенной к боковой стороне.

Ответ: 28

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть M - середина BC, тогда $$BM=2$$.

По теореме косинусов: $$AM^2=AB^2+BM^2-2AB\cdot BM{\cos \angle B\ }$$ т.е. $$AM^2=16+4-2\cdot 4\cdot 2\left(\frac{1}{2}\right)=28$$.

Аналоги к этому заданию:

Задание 7

Прямая $$y=7x+28$$ является касательной к графику функции $$y=ax^2-21x+3a$$. Найдите значение коэффициента $$a$$, если известно, что абсцисса точки касания положительна.

Ответ: 14

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Т. к. касательная, то $$(7x+28)'=(ax^2-21x+3a)'$$ и $$7x+28=ax^2-21x+3a$$.

Получим: $$\left\{ \begin{array}{c} 7=2ax-21 \\ ax^2-28x+3a-28=0 \\ x>0 \end{array} \right.\to $$$$\left\{ \begin{array}{c} a=\frac{14}{x} \\ 14x-28x+\frac{42}{x}-28=0 \\ x>0 \end{array} \right.$$; $$\frac{42}{x}-14x-28=0\to$$$$ -14x^2-28x+42=0\to$$$$ x^2+2x-3=0\to$$

$$\to \left[ \begin{array}{c} x_1=-3<0 \\ x_2=1\to a=\frac{14}{1}=14 \end{array} \right.$$

Аналоги к этому заданию:

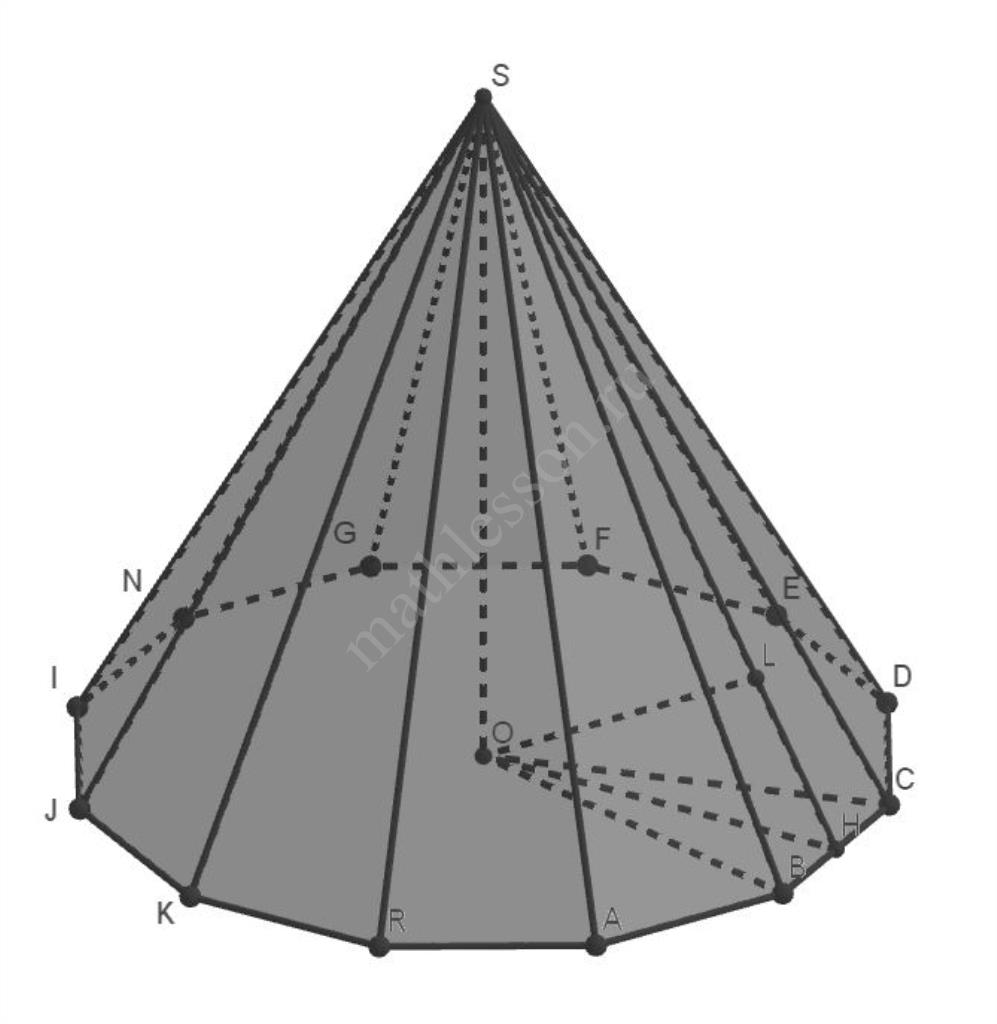
Задание 8

Сторона основания правильной двенадцатиугольной пирамиды равна $$6{tg 15{}^\circ \ }$$, а высота равна 4. Найдите расстояние от центра основания пирамиды до плоскости, содержащей боковую грань пирамиды.

Ответ: 2,4

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\angle A=\frac{\left(12-2\right)\cdot 180}{12}=150\to \angle OCH=75{}^\circ ;$$$$\ \angle COH=15{}^\circ $$. Пусть $$OH\bot CD$$, S - вершина пирамиды.

По теореме о трёх перпендикулярах $$SH\bot CD$$ (SO - высота пирамиды): $$ (SOH)\bot CD\to OL\bot CD$$, где $$OL\bot SH\to OL\bot (SCD)$$ и OL - расстояние.

$$CH=\frac{CD}{2}=3{tg 15{}^\circ \ }\to$$$$ OH=\frac{CH}{{tg COH\ }}=3\to$$$$ SH=\sqrt{SO^2+OH^2}=5\to$$ $$ OL=\frac{SO\cdot OH}{SH}=\frac{4\cdot 3}{5}=2,4.$$

Аналоги к этому заданию:

Задание 9

9. Найдите значение выражения $$\sqrt[4]{{({{\sin }^{{\rm 2}} x\ }-1)}^4}+\sqrt[4]{{({{\cos }^{{\rm 2}} x\ }-3)}^4}$$

Ответ: 3

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть $$\sqrt[4]{{({{\sin }^{{\rm 2}} x\ }-1)}^4}+\sqrt[4]{{({{\cos }^{{\rm 2}} x\ }-3)}^4}=$$$$\left|{{\sin }^{{\rm 2}} x\ }-1\right|+\left|{{\cos }^{{\rm 2}} x\ }-3\right|=$$ $$=1-{{\sin }^{{\rm 2}} x\ }+3-{{\cos }^{{\rm 2}} x\ }=$$$${{\cos }^{{\rm 2}} x\ }+3-{{\cos }^{{\rm 2}} x\ }=3$$

Аналоги к этому заданию:

Задание 10

Скорость колеблющегося на пружине груза меняется по закону $$v\left(t\right)=7{\sin \frac{\pi t}{4}\ }$$ (см/с), где $$t$$ время в секундах. Какую долю времени из первых двух секунд скорость движения превышала 3,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Ответ: 0,67

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть $$\left\{ \begin{array}{c} 7{\sin \frac{\pi t}{4}\ }>3,5 \\ t\in \left[0;2\right] \end{array} \right.\leftrightarrow$$$$ \left\{ \begin{array}{c} {\sin \frac{\pi t}{4}\ }>\frac{1}{2} \\ t\in \left[0;2\right] \end{array} \right.\leftrightarrow$$$$ \left\{ \begin{array}{c} \frac{\pi t}{4}\in (\frac{\pi }{6}+2\pi k;\frac{5\pi }{6}+2\pi k) \\ k\in Z \\ t\in \left[0;2\right] \end{array} \right.\leftrightarrow $$ $$\left\{ \begin{array}{c} t\in \left(\frac{2}{3}+8k;\frac{10}{3}+8k\right),k\in Z\ \\ t\in \left[0;2\right] \end{array} \right.\to $$ т.е. превышало с $$\frac{2}{3}$$ секунды, т.е. $$1\frac{1}{3}$$ времени $$\to \ \frac{\frac{4}{3}}{2}=\frac{2}{3}\approx 0,67$$.

Аналоги к этому заданию:

Задание 11

Две копировальные машины печатают рукопись. Если всю рукопись будет печатать первая машина, то работа будет выполнена на 4 минуты позже, чем две машины, работая вместе. Если печатать всю рукопись будет вторая машина, то она напечатает на 25 минут позже, чем обе машины, работая вместе. За сколько минут может напечатать эту рукопись вторая машина?

Ответ: 35

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Пусть 1 - объем рукописи, x - доля рукописи, которую печатает первая в минуту, y - вторая. Тогда: $$\left\{ \begin{array}{c} \frac{1}{x}=\frac{1}{x+y}+4 \\ \frac{1}{y}=\frac{1}{x+y}+25 \end{array} \right.$$. Вычтем из второго первое: $$\frac{1}{y}-\frac{1}{x}=21\to$$$$ \frac{1}{x}=\frac{1}{y}-21\to$$$$ \frac{1}{x}=\frac{1-21y}{y}\to$$$$ x=\frac{y}{1-21y}$$.

Подставим в первое: $$\frac{1-21y}{y}=\frac{1}{\frac{y}{1-21y}+y}+4\to$$$$ \frac{1-21y}{y}=\frac{1\left(1-21y\right)}{2y-21y^2}+4\to$$ $$ \frac{1-21y}{y}=\frac{1-21y+8y-84y^2}{2y-21y^2}\to $$ $$ 2y-21y^2-42y^2+441y^3=$$$$y-21y^2+8y^2-84y^3\to$$$$ 525y^3-50y^2+y=0$$.

$$y\left(525y^2-50y+1\right)=0\to$$$$ \frac{D}{4}=625-525=100\to $$ $$\left\{ \begin{array}{c} y_1=\frac{25+10}{525}=\frac{1}{15}\to x<0; y_2=\frac{25-10}{525}=\frac{1}{35} \end{array} \right.$$. Получаем, что вторая напечатает за $$\frac{1}{\frac{1}{35}}=35$$ минут.

Аналоги к этому заданию:

Задание 12

Найдите точку минимума функции $$f\left(x\right)={\ln (\frac{x^2+4}{x})\ }$$

Ответ: 2

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть $$f'\left(x\right)=\frac{1}{\frac{x^2+4}{x}}\cdot {\left(\frac{x^2+4}{x}\right)}'=$$$$\frac{x}{x^2+4}{\left(x+\frac{4}{x}\right)}'=$$$$\frac{x}{x^2+4}\left(1-\frac{4}{x^2}\right)=$$ $$=\frac{x^2-4}{x(x^2+4)}=0\to \left[ \begin{array}{c} x=\pm 2 \\ x\ne 0 \end{array} \right.$$ Учтем, что по $$D\left(f\right):\ \frac{x^2+4}{x}>0\to x>0\to x=2$$.

Аналоги к этому заданию:

Задание 13

а) Решите уравнение $${{\log }_2 (x^2-5)\ }\cdot {{\log }^2_3 \left(7-x\right)\ }+3{{\log }_2 \left(x^2-5\right)\ }-2{{\log }^2_3 \left(7-x\right)\ }-6=0$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$\left[{{\log }_2 \frac{1}{7}\ };{{\log }_2 9\ }\right]$$

Ответ: а) $$\pm 3$$; б) 3

Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Аналоги к этому заданию:

Задание 14

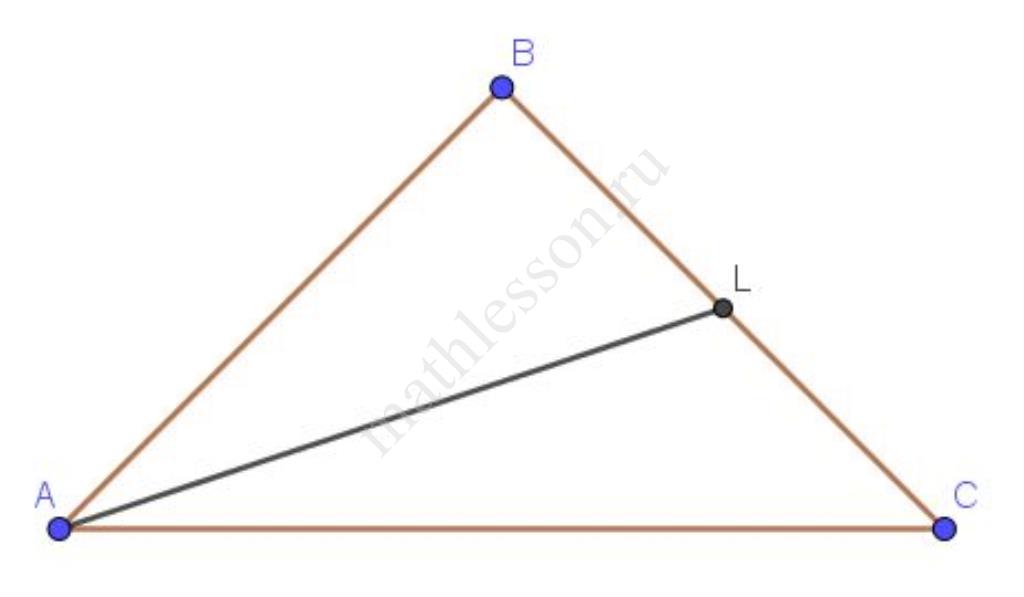
В треугольной пирамиде SABC точка Е - середина ребра SA, точка F - середина ребра SB, О - точка пересечения медиан треугольника АВС

а) Докажите, что плоскость CEF делит отрезок SO в отношении 3:2, считая от вершины S

б) Найдите косинус угла между плоскостями CEF и EFT, если точка Т - середина SC, а пирамида SABC правильная, площадь треугольника АВС равна $$27\sqrt{3},\ SB=10$$.

Ответ: $$\frac{15}{17}$$

Решение 1 Предложить свое решение / сообщить об ошибке

Аналоги к этому заданию:

Задание 15

Решите неравенство: $$\sqrt{4^x-5\cdot 2^{x+1}+25}+\sqrt{9^x-2\cdot 3^{x+2}+17}\le 2^x-5$$

Ответ: $$\log_{3}17$$

Видео-решение Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$\sqrt{4^x-5\cdot 2^{x+1}+25}+\sqrt{9^x-2\cdot 3^{x+2}+17}\le 2^x-5\leftrightarrow$$

$$\sqrt{2^{2x}-10\cdot 2^x+25}+\sqrt{3^{2x}-18\cdot 3^x+17}\le 2^x-5\leftrightarrow$$

$$\sqrt{{{(2}^x-5)}^2}+\sqrt{3^{2x}-18\cdot 3^x+17}\le 2^x-5\to$$ $$\to \left|2^x-5\right|+\sqrt{3^{2x}-18\cdot 3^x+17}\le 2^x-5.$$

Справа неотрицательное число, тогда $$2^x-5\ge 0\to \left|2^x-5\right|=2^x-5$$.

Получим: $$\left\{ \begin{array}{c} \sqrt{3^{2x}-18\cdot 3^x+17}\le 0 \\ 2^x-5\ge 0 \end{array} \right.\to \left\{ \begin{array}{c} \left(3^x-17\right)\left(3^x-1\right)=0 \\ 2^x-5\ge 0 \end{array} \right.\leftrightarrow$$

$$\left\{ \begin{array}{c} \left[ \begin{array}{c} x={{\log }_3 17\ } \\ x=0 \end{array} \right. \\ 2^x-5\ge 0 \end{array} \right.$$.

Сравним $${{\log }_3 17\ }$$ и $${{\log }_2 5\ }$$:

:

$${{\log }_3 17\ }={{\log }_3 9\ }+{{\log }_3 \frac{17}{9}\ }=2+{{\log }_3 1,8\ }>2,5$$

$${{\log }_2 5\ }={{\log }_2 4\ }+{{\log }_2 1,25\ }<2,5\to в\ ответ\ {{\log }_3 17\ }$$

Аналоги к этому заданию:

Задание 16

Точка $$O_1$$ - центр вписанной окружности равнобедренного треугольника АВС, а $$O_2$$ - центр вневписанной окружности, касающейся основания ВС.

а) Докажите, что расстояние от середины отрезка $$O_1O_2$$ до точки С вдвое меньше $$O_1O_2$$.

б) Известно, что радиус первой окружности в пять раз меньше радиуса второй. В каком отношении точка касания первой окружности с боковой стороной треугольника делит эту сторону?

Ответ: 1:2

Решение 1 Предложить свое решение / сообщить об ошибке

Аналоги к этому заданию:

Задание 17

Борис и Иван вложили деньги в общий бизнес. После этого один из них добавил еще 1 миллион рублей, в результате чего его доля в бизнесе увеличилась на 0,05, а когда он добавил еще 1 миллион рублей, его доля увеличилась еще на 0,04. Сколько миллионов рублей ему еще нужно добавить, чтобы увеличить свою долю еще на 0,06?

Ответ: 2

Видео-решение Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть Пусть x - сумма того, кто увеличивает, S - начальная сумма: $$\left\{ \begin{array}{c} \frac{x+1}{S+1}-\frac{x}{S}=0,05 \\ \frac{x+2}{S+2}-\frac{x+1}{S+1}=0,04 \end{array} \right.\leftrightarrow$$ $$\left\{ \begin{array}{c} \frac{Sx+S-Sx-x}{S(S+1)}=\frac{5}{100} \\ \frac{Sx+x+2S+2-Sx-S-2x-2}{(S+1)(S+2)}=\frac{4}{100} \end{array} \right.\leftrightarrow$$ $$\left\{ \begin{array}{c} \frac{S-x}{S(S+1)}=\frac{5}{100} \\ \frac{S-x}{(S+1)(S+2)}=\frac{4}{100} \end{array} \right.$$ Поделим первое на второе: $$\frac{S+2}{S}=\frac{5}{4}\to 4S+8=5S\to S=8\to$$ $$\frac{x+1}{9}-\frac{x}{8}=\frac{5}{100}\to $$ $$\to 8x+8-9x=3,6\to x=4,4\to \frac{4,4}{8}=0,55$$. Тогда y - третья сумма добавления: $$\frac{6,4+y}{10+y}=0,55+0,05+0,04+0,06=0,7\to$$ $$64+10y=70+7y\to 3y=6\to y=2$$ миллиона надо добавить.

Аналоги к этому заданию:

Задание 18

Найдите все значения параметра $$a$$, при которых система уравнений

$$\left\{ \begin{array}{c} \sqrt{4-2x+y}=2 \\ a{\left(x^2+3y+1\right)}^2-\left(a+1\right)\left(x^2+3y+1\right)-2a-1=0 \end{array} \right.$$

имеет не более 3 решений.

Ответ: {$$-\frac{1}{3}$$};[$$-\frac{1}{10};0$$]

Решение 1 Решение 2 Решение 3 Предложить свое решение / сообщить об ошибке

Аналоги к этому заданию:

Задание 19

На доске было написано 30 натуральных чисел (необязательно различных), каждое из которых больше 2, но не превосходит 42. Среднее арифметическое написанных чисел равнялось 6. Вместо каждого из чисел на доске написали число, в два раза меньше первоначального. Числа, которые после этого оказались меньше 2, с доски стерли.

а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся на доске, больше 10?

б) Могло ли среднее арифметическое оставшихся на доске оказаться больше 8, но меньше 9?

в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.

Ответ: а) да; б) нет; в) 16,5

Решение 1 Решение 2 Решение 3 Предложить свое решение / сообщить об ошибке

Скрыть