ЕГЭ математика 2017. Разбор варианта Алекса Ларина № 198



Подробный разбор 1,2,3,4,5,6,7,8,9,10,11,12 задания вариант ЕГЭ Ларина № 198

Подробный разбор 13,14,15,16,17,18,19 задания вариант ЕГЭ Ларина № 198

 
Аналоги к этому заданию:

Задание 1

Альбом для рисования стоит 30 рублей. Какое наибольшее число таких альбомов можно будет купить на 500 рублей во время акции, где на все канцтовары действует скидка 15%?

Ответ: 19
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) Скидка действует 15%, значит заплатить придется 100-15=85% от основной суммы: 30 - 100% x - 85% x = 30 * 85 / 100 = 25.5 2) 500/25.5=19.6 ( если округлить ) , значит можно купить 19 тетрадей

 
Аналоги к этому заданию:

Задание 2

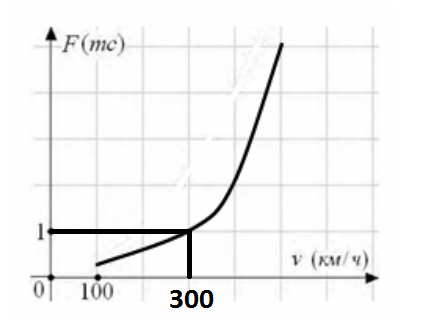
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 300 км/ч?

Ответ: 1
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

На рисунке видно, что подъемная сила в данном случае будет равна 1

 
Аналоги к этому заданию:

Задание 3

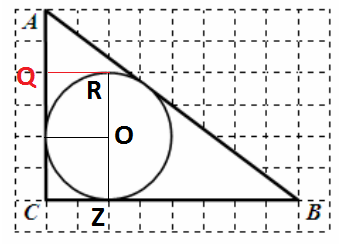
Найдите радиус окружности, вписанной в треугольник АВС, если размер клетки 1 см х 1 см. Ответ дайте в сантиметрах.

Ответ: 2
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1 Вариант

Находим диаметр - RZ, он равен QZ = 4 . Значит радиус вписанной равен 2

2 Вариант

По теореме Пифаогора найдем AB = 10

Найдем полупериметр $$p = \frac{10+8+6}{2}=12$$

Найдем площадь через половину произведения катетов $$S = \frac{1}{2}6*8=24$$

Найдем радиус вписанной окружности $$ r = \frac{S}{p}=\frac{24}{12}=2$$

 
Аналоги к этому заданию:

Задание 4

В супермаркете стоят три банкомата. Каждый из них может быть неисправен с вероятностью 0,2 независимо от других. Найдите вероятность того, что в супермаркете ровно два банкомата окажутся в рабочем состоянии .

Ответ: 0.384
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Вероятность того, что банкомат окажется в рабочем состоянии, противоположна нерабочему состоянию, а значит равна 1 - 0,2 = 0,8

Так как у нас независимо друг от друга вероятности банкоматов существуют, то вероятность того, что два исправны выглядит так ( И - исправен, Н - неисправен, 1,2,3 - номера банкоматов ):

1 2 3 вероятность
И И Н 0,8*0,8*0,2=0,128
И Н И 0,8*0,2*0,8=0,128
Н И И 0,2*0,8*0,8=0,128

Следовательно, конечная вероятность равна сумме полученных: 0.128 * 3 = 0.384

Аналоги к этому заданию:

Задание 5

В прямоугольном треугольнике АВС угол С – прямой. СН – высота, СL – биссектриса, ∠ А = 39. Найдите ∠ НСL. Ответ дайте в градусах.

 

Ответ: 6
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как CH - высота, то треугольники ACH и CBH подобны, а значит ∠HCB=∠CAH=39
В таком случае ∠ACH = 90 - ∠HCB = 90 - 39 = 51
∠ ACL = 90 / 2 = 45 ( так как CL биссектриса )
Тогда ∠LCH = ∠ACH - ∠ACL = 51 - 45 = 6
 
Аналоги к этому заданию:

Задание 6

На рисунке приведен график f ' (x) – производной функции у = f (x). Определите абсциссу точки графика функции у = f (x), в которой касательная параллельна прямой у = 2х – 1 или совпадает с ней.

Ответ: -3
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Так как касательная к графику параллельна или совпадает с прямой y = 2x - 1, и при этом значение производной равно коэффициенту k линейной функции ( в нашем случае этот коэффициент равен 2 ), то и значение производной, которое мы ищем, равно 2. А так как нам дан график производной, то мы смело находим точку с ординатой (ось Оу) равную 2 и ищем абсциссу этой точки. Она равна -3

 
Аналоги к этому заданию:

Задание 7

В кубе с ребром, равным 3, сделано сквозное отверстие размером 1 х 1. Найдите площадь полной поверхности полученного многогранника.

 

Ответ: 64
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь поверхности самого куба равна 3*3*6=54. Из него вычитаем два окошка , каждое из которых 1*1 = 1. То есть остается 54 - 2 = 52.
Но так же надо прибавить площади появившихся граней внутри куба. Каждая из них прямоугольник со сторонами 3 и 1 . Значит площадь 3*1=3. Их 4 штуки, а значит 3*1*4=12
В итоге площадь поверхности многогранника будет 52+12=64
 
Аналоги к этому заданию:

Задание 8

Известно, что $$ tg x = \frac{2}{\sqrt{21}}$$ и $$\pi < x< \frac{3\pi }{2}$$. Найдите sin x

Ответ: -0.4
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Угол располагается в третьей четверти, поэтому sin будет отрицательный. Найдем сначала ctg x: $$ ctg x = \frac {1}{tg x}= \frac {1}{\frac{2}{\sqrt{21}}}=\frac{\sqrt{21}}{2}$$ Выразим sin x из формулы $$ 1 + ctg^{2} x = \frac{1}{\sin^{2} x} $$ $$ \frac{1}{1 + ctg^{2} x} =\sin^{2} x $$ $$\sin x = - \sqrt{ \frac{1}{1 + ctg^{2} x} } $$ $$\sin x = - \sqrt{ \frac{1}{1 + (\frac{\sqrt{21}}{2})^{2}} }=- \sqrt{ \frac{1}{1 + \frac{21}{4}}}=-\frac{2}{5}=-0.4 $$

 
Аналоги к этому заданию:

Задание 9

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: FA= αρgr3, где α=4,2 – постоянная, r – радиус аппарата в метрах, ρ=1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g=10 Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336000 Н? Ответ выразите в метрах.

Ответ: 2
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

Подставим имеющиеся значения в формулу: $$336000=4.2*1000*10*r^{3}$$ $$r^{3}=\frac{336000}{4.2*1000*10}=8$$ r = 2

 
Аналоги к этому заданию:

Задание 10

Первые пять часов автомобиль ехал со скоростью 60 км/ч, следующие 246 км он преодолел за 3 часа, а последние 130 км проехал со скоростью 65 км/ч. Найдите среднюю скорость (в км/ч) автомобиля на всем пути.

Ответ: 67.6
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
За первые пять часов он проехал 60 * 5 = 300 км
Последние 130 км он ехал $$\frac{130}{65}=2$$ ч
Тогда средняя скорость будет равна $$\frac{300+246+130}{5+3+2}=67.6$$
 
Аналоги к этому заданию:

Задание 11

Найдите точку максимума функции $$f(x)=24-3x^{4}-8x{3}$$

Ответ: -2
Видео-решение Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную функции и приравняем ее к нулю:
$$f'(x)=-12x^{3}-24x^{2}=0$$
$$f'(x)=-12x^{2}(x+2)=0$$
Получаем или x = 0, или x = -2.
Отметим эти точки на координатной прямой и расставим знаки производной:
Как видим, точка максимум -2
 
Аналоги к этому заданию:

Задание 12

Дано уравнение $$\cos^{2}x(tg(\frac{9\pi}{2}+x)-3tg^{2}(\pi-x))=\cos 2x-1$$

А) Решите уравнение.
Б) Найдите его корни, принадлежащие промежутку $$[-4;-1]$$.
Ответ: А)$$-\frac{\pi}{4}+\pi n,n \in Z$$ Б)$$-\frac{5\pi}{4}$$
Решение 1 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 13

В основании прямой призмы $$ABCA_{1}B_{1}C_{1}$$ лежит равнобедренный треугольник $$ABC$$, в котором $$AB=AC$$.

А) Докажите, что объем пирамиды $$A_{1}BCC_{1}B_{1}$$ составляет 2/3 объема призмы.
Б) Найдите радиус сферы, описанной около пирамиды $$A_{1}BCC_{1}B_{1}$$, если известно, что $$AB=5$$, $$BC=6$$, $$AA_{1}=15$$.
Ответ: $$\frac{65}{8}$$
Решение 1 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 14

Решите неравенство $$4\cdot\log_{2}(8-2^{1+x^{2}})-\log_{2}^{2}(2^{3-x^{2}}-2)\leq 4x^{2}+3$$

Ответ: $$(-\sqrt{2};-1];[1;\sqrt{2})$$
Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 15

В треугольнике $$ABC$$ проведена биссектриса $$BK$$ и на сторонах $$BA$$ и $$BC$$ взяты соответственно точки $$M$$ и $$P$$Р так, что $$\angle AKM=\angle CKP=\frac{1}{2}\angle ABC$$

а) Докажите, что прямая $$AC$$ касается окружности, описанной около треугольника $$MBP$$.
б) Найдите радиус окружности, описанной около треугольника $$MBP$$, если известно, что $$AB=10$$, $$BC=15$$, $$AC=20$$.
Ответ: $$\frac{24\sqrt{15}}{25}$$
Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 16

1 мая 2017 г. Татьяна Константиновна положила 10 000 000 рублей в банк сроком на 1 год с ежемесячным начислением процентов и капитализацией под а % годовых. Это означает, что первого числа каждого месяца сумма вклада увеличивается на одно и то же количество процентов, рассчитанное таким образом, что за 12 месяцев она увеличится ровно на $$a$$ %. Найдите $$a$$, если известно, что через 6 месяцев сумма вклада Татьяны Константиновны составила 10 400 000 рублей.

Ответ: 8,16
Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 17

Найдите все $$a$$, при каждом из которых система $$\left\{\begin{matrix} y^2-2x^2+xy+9x-9=0\\ ax^2+2ax-y-3+a=0 \end{matrix}\right.$$ имеет ровно четыре различных решения

Ответ: $$(-\frac{1}{8};0);(0;\frac{2}{9});(\frac{2}{9};\frac{1}{4})$$
Решение 1 Решение 2 Предложить свое решение / сообщить об ошибке
 
Аналоги к этому заданию:

Задание 18

Государство Новая Анчурия расположено на острове, имеющем форму круга. В стране 11 городов, расположенных на побережье. Каждый город напрямую соединен с каждым из остальных городов автотрассой.

А) Сколько автотрасс в государстве Новая Анчурия?
Б) После наводнения несколько автотрасс в стране закрыли на ремонт. Могло ли оказаться так, что теперь каждый город острова стал напрямую соединен автотрассой ровно с пятью другими городами?
В) Какое наибольшее число автотрасс в Новой Анчурии можно одновременно закрыть на ремонт, чтобы из каждого города можно было добраться на автомобиле до любого другого?
Ответ: А)55 Б)Нет В)45
Решение 1 Предложить свое решение / сообщить об ошибке
Скрыть

а) Из каждого города выходит 10 дорог, поэтому всего есть 10 умножить на 11=110 концов дорог. Значит, дорог 55.

б) Если теперь из каждого города выходит 5 дорог, то всего есть 5 умножить на 11=55 концов дорог. Значит, дорог 27,5, что невозможно.

в) Можно оставить 10 дорог (например, соединяющих столицу со всеми городами, тогда откуда угодно куда угодно можно будет проехать через столицу), поэтому удастся закрыть 45.

Если оставить всего n-2 или меньше дорог на n городов, то это будет невозможно. В самом деле, у n-2 дорог 2n-4 конца, поэтому найдется город (на самом деле даже минимум 4 таких города) из которых выходит по одной дороге (0 дорог быть не может, из него тогда никуда нельзя доехать). Ясно, что проезжать транзитом через такой город нельзя. Поэтому если мысленно убрать с карты этот город и эту дорогу, на остальной карте можно будет проехать от любого города до любого другого. При этом число дорог снова на 2 меньше числа городов. Продолжая эти действия, придем к ситуации 0 дорог и 2 города, которая нам не подходит.